Difference between revisions of "Aufgaben:Exercise 4.10: Binary and Quaternary"
From LNTwww
| (3 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
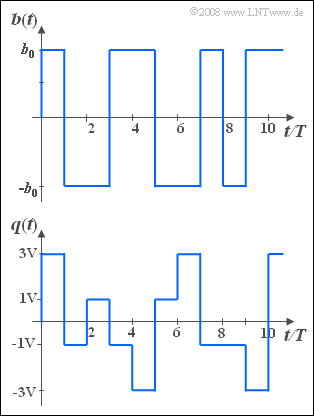
| − | [[File:P_ID384__Sto_A_4_10.png|right|300px|frame|Binary signal $b(t)$ | + | [[File:P_ID384__Sto_A_4_10.png|right|300px|frame|Binary signal $b(t)$, quaternary signal $q(t)$]] |
| − | We consider here a binay signal $b(t)$ and a quaternary | + | We consider here a binay signal $b(t)$ and a quaternary signal $q(t)$. |
| − | *The two signals are rectangular in shape | + | *The two signals are rectangular in shape. The duration of each rectangle is $T$ (symbol duration). |
*The symbols represented by the pulse heights of the individual rectangular pulses $($with step number $M = 2$ or $M = 4)$ are statistically independent. | *The symbols represented by the pulse heights of the individual rectangular pulses $($with step number $M = 2$ or $M = 4)$ are statistically independent. | ||
| − | *Because of the bipolar signal constellation, both signals | + | *Because of the bipolar signal constellation, both signals have no DC component if the symbol probabilities are chosen appropriately (symmetrically). |
| − | *Because of the latter property, it follows for the probabilities of the binary symbols: | + | *Because of the latter property, it follows for the probabilities of the binary symbols: |
:$${\rm Pr}\big[b(t) = +b_0\big] = {\rm Pr}\big[b(t) = -b_0\big] ={1}/{2}.$$ | :$${\rm Pr}\big[b(t) = +b_0\big] = {\rm Pr}\big[b(t) = -b_0\big] ={1}/{2}.$$ | ||
| − | *In contrast, for the quarternary signal: | + | *In contrast, for the quarternary signal: |
:$${\rm Pr}\big[q(t) = +3 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -3 \hspace{0.05cm}{\rm V}\big]= {1}/{6},$$ | :$${\rm Pr}\big[q(t) = +3 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -3 \hspace{0.05cm}{\rm V}\big]= {1}/{6},$$ | ||
:$${\rm Pr}\big[q(t) = +1 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -1 \hspace{0.05cm}{\rm V}\big]= {2}/{6}.$$ | :$${\rm Pr}\big[q(t) = +1 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -1 \hspace{0.05cm}{\rm V}\big]= {2}/{6}.$$ | ||
| − | + | '''Hint''': This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-Correlation Function]]. | |
| − | |||
| − | |||
| − | Hint: | ||
| − | |||
| Line 27: | Line 23: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Calculate the ACF | + | {Calculate the ACF value $\varphi_q(\tau = 0)$ of the quaternary signal. |
|type="{}"} | |type="{}"} | ||
$\varphi_q(\tau = 0) \ = \ $ { 3.667 3% } $\ \rm V^2$ | $\varphi_q(\tau = 0) \ = \ $ { 3.667 3% } $\ \rm V^2$ | ||
| − | {What is the magnitude of the ACF | + | {What is the magnitude of the ACF value when $\tau = T$ ? Justify why the ACF values for $|\tau| > T$ are of the same size. Sketch the ACF diagram. |
|type="{}"} | |type="{}"} | ||
$\varphi_q(\tau = T) \ = \ $ { 0. } $\ \rm V^2$ | $\varphi_q(\tau = T) \ = \ $ { 0. } $\ \rm V^2$ | ||
| Line 38: | Line 34: | ||
| − | {With which amplitude values $(\pm b_0)$ does the binary signal $b(t)$ have exactly the same | + | {With which amplitude values $(\pm b_0)$ does the binary signal $b(t)$ have exactly the same ACF? |
|type="{}"} | |type="{}"} | ||
$b_0\ = \ $ { 1.915 3% } $\ \rm V$ | $b_0\ = \ $ { 1.915 3% } $\ \rm V$ | ||
| − | {Which of the following descriptive quantities of a stochastic process can be determined from the | + | {Which of the following descriptive quantities of a stochastic process can be determined from the ACF? |
|type="[]"} | |type="[]"} | ||
+ Period duration. | + Period duration. | ||
| Line 58: | Line 54: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The ACF value at the point $\tau = 0$ corresponds to the mean signal power, i.e. the | + | '''(1)''' The ACF value at the point $\tau = 0$ corresponds to the mean signal power, i.e. the variance of $q(t)$. For this holds: |
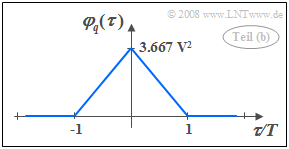
| − | [[File:P_ID385__Sto_A_4_10_b_neu.png|right|frame|Triangular | + | [[File:P_ID385__Sto_A_4_10_b_neu.png|right|frame|Triangular auto-correlation function]] |
:$$\varphi_q(\tau = 0)= {1}/{6 } \cdot ({\rm 3\,V})^2 + {2}/{6 } \cdot ({\rm 1\,V})^2 + {2}/{6 } \cdot (-{\rm 1\,V})^2 + {1}/{6 } \cdot (-{\rm 3\,V})^2= \rm {22}/{6 }\, \rm V^2\hspace{0.15cm}\underline{= \rm 3.667 \,V^2}.$$ | :$$\varphi_q(\tau = 0)= {1}/{6 } \cdot ({\rm 3\,V})^2 + {2}/{6 } \cdot ({\rm 1\,V})^2 + {2}/{6 } \cdot (-{\rm 1\,V})^2 + {1}/{6 } \cdot (-{\rm 3\,V})^2= \rm {22}/{6 }\, \rm V^2\hspace{0.15cm}\underline{= \rm 3.667 \,V^2}.$$ | ||
'''(2)''' The individual symbols were assumed to be statistically independent. | '''(2)''' The individual symbols were assumed to be statistically independent. | ||
| − | *Therefore, and because of the lack of a DC component, for any integer value of $\nu$, the following applies here: | + | *Therefore, and because of the lack of a DC component, for any integer value of $\nu$, the following applies here: |
:$${\rm E} \big [ q(t) \cdot q ( t + \nu T) \big ] = {\rm E} \big [ q(t) \big ] \cdot {\rm E} \big [ q ( t + \nu T) \big ]\hspace{0.15cm}\underline{ = 0}.$$ | :$${\rm E} \big [ q(t) \cdot q ( t + \nu T) \big ] = {\rm E} \big [ q(t) \big ] \cdot {\rm E} \big [ q ( t + \nu T) \big ]\hspace{0.15cm}\underline{ = 0}.$$ | ||
| − | *Thus, the ACF we are looking for has the shape sketched on the right. | + | *Thus, the ACF we are looking for has the shape sketched on the right. |
| − | *In the range $-T \le \tau \le +T$ the ACF is sectionwise linear, i.e. triangular, due to the rectangular pulse shape. | + | *In the range $-T \le \tau \le +T$ the ACF is sectionwise linear, i.e. triangular, due to the rectangular pulse shape. |
<br clear=all> | <br clear=all> | ||
| − | '''(3)''' The ACF $\varphi_b(\tau)$ of the binary signal is also identically zero due to the statistically independent symbols in the range $| \tau| > T$ | + | '''(3)''' The ACF $\varphi_b(\tau)$ of the binary signal is also identically zero due to the statistically independent symbols in the range $| \tau| > T$. |
| − | *For the | + | *For $-T \le \tau \le +T$ itnalso results in a triangular shape. |
| + | *For the second moment, one obtains: | ||
:$$\varphi_b (\tau = 0) = b_{\rm 0}^{\rm 2}.$$ | :$$\varphi_b (\tau = 0) = b_{\rm 0}^{\rm 2}.$$ | ||
| − | *With $b_0\hspace{0.15cm}\underline{= 1.915\, \rm V}$ the two | + | *With $b_0\hspace{0.15cm}\underline{= 1.915\, \rm V}$ the two auto-correlation functions $\varphi_q(\tau)$ and $\varphi_b(\tau)$ are identical. |
| − | '''(4)''' Correct are <u>the proposed solutions 1, 3, and 4</u>. | + | '''(4)''' Correct are <u>the proposed solutions 1, 3, and 4</u>. |
From the autocorrelation function we can actually determine: | From the autocorrelation function we can actually determine: | ||
| − | * | + | *The period $T_0$: this is the same for the pattern signals and the ACF; |
| − | * the linear mean: root of the final value of the ACF for $\tau \to \infty$ | + | * the linear mean: root of the final value of the ACF for $\tau \to \infty$; |
* the variance: difference of the ACF values of $\tau = 0$ and $\tau \to \infty$. | * the variance: difference of the ACF values of $\tau = 0$ and $\tau \to \infty$. | ||
Cannot be determined: | Cannot be determined: | ||
| − | * | + | * The probability density function $\rm (PDF)$: <br> despite $\varphi_q(\tau) =\varphi_b(\tau)$ ⇒ $f_q(q) \ne f_b(b)$; |
| − | * the moments of higher order: for their calculation one needs the PDF; | + | * the moments of higher order: <br> for their calculation one needs the PDF; |
| − | * | + | * all phase relations and symmetry properties are not recognizable from the ACF. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 14:20, 18 January 2023
We consider here a binay signal $b(t)$ and a quaternary signal $q(t)$.
- The two signals are rectangular in shape. The duration of each rectangle is $T$ (symbol duration).
- The symbols represented by the pulse heights of the individual rectangular pulses $($with step number $M = 2$ or $M = 4)$ are statistically independent.
- Because of the bipolar signal constellation, both signals have no DC component if the symbol probabilities are chosen appropriately (symmetrically).
- Because of the latter property, it follows for the probabilities of the binary symbols:
- $${\rm Pr}\big[b(t) = +b_0\big] = {\rm Pr}\big[b(t) = -b_0\big] ={1}/{2}.$$
- In contrast, for the quarternary signal:
- $${\rm Pr}\big[q(t) = +3 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -3 \hspace{0.05cm}{\rm V}\big]= {1}/{6},$$
- $${\rm Pr}\big[q(t) = +1 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -1 \hspace{0.05cm}{\rm V}\big]= {2}/{6}.$$
Hint: This exercise belongs to the chapter Auto-Correlation Function.
Questions
Solution
(1) The ACF value at the point $\tau = 0$ corresponds to the mean signal power, i.e. the variance of $q(t)$. For this holds:
- $$\varphi_q(\tau = 0)= {1}/{6 } \cdot ({\rm 3\,V})^2 + {2}/{6 } \cdot ({\rm 1\,V})^2 + {2}/{6 } \cdot (-{\rm 1\,V})^2 + {1}/{6 } \cdot (-{\rm 3\,V})^2= \rm {22}/{6 }\, \rm V^2\hspace{0.15cm}\underline{= \rm 3.667 \,V^2}.$$
(2) The individual symbols were assumed to be statistically independent.
- Therefore, and because of the lack of a DC component, for any integer value of $\nu$, the following applies here:
- $${\rm E} \big [ q(t) \cdot q ( t + \nu T) \big ] = {\rm E} \big [ q(t) \big ] \cdot {\rm E} \big [ q ( t + \nu T) \big ]\hspace{0.15cm}\underline{ = 0}.$$
- Thus, the ACF we are looking for has the shape sketched on the right.
- In the range $-T \le \tau \le +T$ the ACF is sectionwise linear, i.e. triangular, due to the rectangular pulse shape.
(3) The ACF $\varphi_b(\tau)$ of the binary signal is also identically zero due to the statistically independent symbols in the range $| \tau| > T$.
- For $-T \le \tau \le +T$ itnalso results in a triangular shape.
- For the second moment, one obtains:
- $$\varphi_b (\tau = 0) = b_{\rm 0}^{\rm 2}.$$
- With $b_0\hspace{0.15cm}\underline{= 1.915\, \rm V}$ the two auto-correlation functions $\varphi_q(\tau)$ and $\varphi_b(\tau)$ are identical.
(4) Correct are the proposed solutions 1, 3, and 4.
From the autocorrelation function we can actually determine:
- The period $T_0$: this is the same for the pattern signals and the ACF;
- the linear mean: root of the final value of the ACF for $\tau \to \infty$;
- the variance: difference of the ACF values of $\tau = 0$ and $\tau \to \infty$.
Cannot be determined:
- The probability density function $\rm (PDF)$:
despite $\varphi_q(\tau) =\varphi_b(\tau)$ ⇒ $f_q(q) \ne f_b(b)$; - the moments of higher order:
for their calculation one needs the PDF; - all phase relations and symmetry properties are not recognizable from the ACF.