Difference between revisions of "Aufgaben:Exercise 4.10: Signal Waveforms of the 16-QAM"

Latest revision as of 17:20, 23 January 2023

Signal waveforms of 16–QAM for
four typical symbols

Let us consider the 16–QAM method according to the block diagram in the theory section.

Very briefly, it can be described as follows:

After serial-parallel conversion and subsequent signal space assignment, four bits of the binary redundancy-free source signal $q(t)$ at the input each result in a complex-valued amplitude coefficient

$$a = a_{\rm I} +{\rm j} · a_{\rm Q}.$$

With the rectangular transmission pulse $g_s(t)$ in the range from $0$ to $T$ and of height $g_0$, after multiplication with the cosine function or minus-sine function in the given time interval, we obtain:

$$s_{\rm cos}(t) = a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.05cm},$$

$$ s_{\rm -sin}(t) = -a_{\rm Q} \cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.05cm}.$$

The 16-QAM transmitted signal is then the sum of these two component signals:

$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$

The graph shows the signals $s_{\rm cos}(t)$, $s_{\rm –sin}(t)$ and $s(t)$ for four selected symbols. Using these, the amplitude coefficients are to be determined.

Hints:

This exercise belongs to the chapter "Quadrature Amplitude Modulation".
The page "Signal waveforms for 4–QAM" is helpful for completing this exercise.
The signal space allocation considered can be seen in Exercise 4.10Z. The color highlights also correspond.
From question (6) onwards, use the parameter values $g_0 = 1 \ \rm V$ and $T = 1 \ \rm µ s$.
Energy values are to be given in $\rm V^2s$ ; like this, they refer to the reference resistance $R = 1 \ \rm \Omega$.

Questions

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

$s_0/g_0 \ = \ $

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

$E_\text{S, max} \ = \ $

$\ \cdot 10^{-6} \ \rm V^2 s$

$E_\text{B, max} \ = \ $

$\ \cdot 10^{-6} \ \rm V^2 s$

$E_\text{B, min} \ = \ $

$\ \cdot 10^{-6} \ \rm V^2 s$

Solution

(1) From the (red) inphase signal ⇒ the real part follows (first equation according to the definition, second equation according to the graph):

$$ s_{\rm cos}(t)= a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)= g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm I}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$

Accordingly, we recognize from the quadrature signal ⇒ imaginary part:

$$ s_{\rm -sin}(t)= -a_{\rm Q}\cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)= -g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm Q}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$

(2) The two partial signals each have the (maximum) envelope $g_0$, while $s_0$ characterizes the transmitted signal $s(t)$.

As can be seen from the signal space allocation (see Exercise 4.10Z) :

$${s_0}/{ g_0 }= \sqrt{2}\hspace{0.15cm}\underline { = 1.414} \hspace{0.05cm}.$$

(3) The amplitude coefficients $a_{\rm I}$ and $a_{\rm Q}$ have the same signs as in subtask (1), but with smaller magnitude:

$$a_{\rm I} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$

(4) In the third (green) interval, we can see a minus-cosine signal with amplitude $g_0$ and a minus-sine signal with amplitude $g_0/3$:

$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$

As is yet to be calculated in sub-task (4) of Exercise 4.10Z, here the magnitude is equal to $|a| =1.054$ and the phase angle is ${\rm arc} \ a \approx 161^\circ$.

(5) The violet signal does not differ from the green interval in the in-phase component except in the sign of the quadrature component:

$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = - 1/3\hspace{0.15cm}\underline {= -0.333} \hspace{0.05cm}.$$

(6) The maximum signal energy occurs when one of the four outer vertices is occupied. In that case:

$$ E_{\rm S, \hspace{0.05cm}max} = {1}/{2}\cdot s_0^2 \cdot T = {1}/{2}\cdot \left (\sqrt{2} \cdot g_0 \right )^2 \cdot T = g_0^2 \cdot T = (1\,{\rm V})^2 \cdot (1\,{\rm \mu s}) \hspace{0.15cm}\underline {= 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$

The average signal energy is equal to the maximum value when only the corner points of the signal space mapping are occupied and the "inner symbols" are excluded from the encoding.

(7) Four bits are transmitted per symbol. From this it follows that:

$$ E_{\rm B, \hspace{0.05cm}max} = {E_{\rm S, \hspace{0.05cm}max}}/{4}\hspace{0.15cm}\underline {= 0.25 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$

(8) The minimum signal energy is obtained at one of the inner signal space points and is smaller by a factor of $9$ than in subtask (7):

$$E_{\rm B, \hspace{0.05cm}min} = \frac{E_{\rm B, \hspace{0.05cm}max}}{9} = \frac{g_0^2 \cdot T}{36} \hspace{0.15cm}\underline { \approx 0.028 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$

In the theory section, it was shown that, assuming all symbols are equally likely, the average signal energy per bit for 16-QAM is approximately:

$$E_{\rm B} \approx 0.139 · g_0^2 \cdot T = 0.035 \cdot 10^{-6}\,{\rm V^2s}.$$

@@ Line 4: / Line 4: @@
 }}
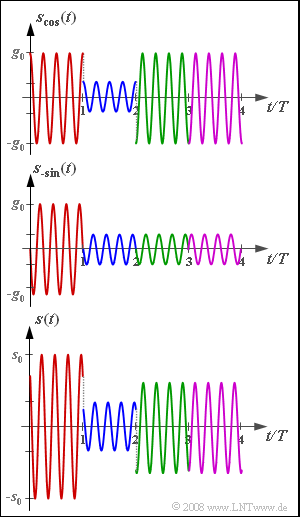
-[[File:P_ID1718__Mod_A_4_9.png|right|]]
+[[File:P_ID1718__Mod_A_4_9.png|right|frame|Signal waveforms of 16–QAM for <br>four typical symbols]]
-Wir betrachten das 16–QAM–Verfahren gemäß dem [http://en.lntwww.de/Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation#Allgemeine_Beschreibung_und_Signalraumzuordnung_.281.2 Blockschaltbild] im Theorieteil. In aller Kürze lässt sich dieses wie folgt beschreiben:
+Let us consider the 16–QAM method according to the [[Modulation_Methods/Quadrature_Amplitude_Modulation#General_description_and_signal_space_allocation|block diagram]]&nbsp; in the theory section.
-:* Jeweils vier Bit des binären redundanzfreien Quellensignals $q(t)$ am Eingang ergeben nach Seriell–Parallell–Wandlung und der folgenden Signalraumzuordnung einen komplexwertigen Amplitudenkoeffizienten $a = a_I + j · a_Q$.
-:* Mit dem rechteckförmigen Sendegrundimpuls $g_s(t)$ im Bereich von 0 bis T und der Höhe $g_0$ erhält man nach den Multiplikationen mit der Cosinus–Funktion bzw. Minus–Sinus–Funktion im betrachteten Zeitintervall:
-$$s_{\rm cos}(t)  =  a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.05cm},$$
-$$ s_{\rm -sin}(t) =  -a_{\rm Q} \cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.05cm}.$$
-:* Das 16–QAM–Sendesignal ergibt sich dann als Summe dieser beiden Komponentensignale:
-$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$
-Die Grafik zeigt für vier ausgewählte Symbole die Signale $s_{cos}(t)$, $s{–sin}(t)$ und $s(t)$. Daraus sollen die Amplitudenkoeffizienten ermittelt werden.
-'''Hinweis:''' Die Aufgabe bezieht sich auf das [http://en.lntwww.de/Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation Kapitel 4.3]. Die betrachtete Signalraumzuordnung ist im Angabenblatt zur [http://en.lntwww.de/Aufgaben:4.9Z_16%E2%80%93QAM%E2%80%93Signalraumkonstellation Aufgabe Z4.9] zu sehen. Auch die farblichen Hervorhebungen passen zusammen. Verwenden Sie ab der Teilaufgabe f) die Zahlenwerte $g_0 = 1 V$ und $T = 1 μs$.
+Very briefly,&nbsp; it can be described as follows:
-===Fragebogen===
+*After serial-parallel conversion and subsequent signal space assignment,&nbsp; four bits of the binary redundancy-free source signal &nbsp;$q(t)$&nbsp; at the input each result in a complex-valued amplitude coefficient
+:$$a = a_{\rm I} +{\rm j} · a_{\rm Q}.$$
+*With the rectangular transmission pulse &nbsp;$g_s(t)$&nbsp; in the range from &nbsp;$0$&nbsp; to &nbsp;$T$&nbsp; and of height &nbsp;$g_0$,&nbsp; after multiplication with the cosine function or minus-sine function in the given time interval,&nbsp; we obtain:
+:$$s_{\rm cos}(t)  =  a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.05cm},$$
+:$$ s_{\rm -sin}(t) =  -a_{\rm Q} \cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.05cm}.$$
+* The 16-QAM transmitted signal is then the sum of these two component signals:
+:$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$
+The graph shows the signals &nbsp;$s_{\rm cos}(t)$, &nbsp;$s_{\rm –sin}(t)$&nbsp; and &nbsp;$s(t)$ for four selected symbols.&nbsp; Using these,&nbsp; the amplitude coefficients are to be determined.
+Hints:
+*This exercise belongs to the chapter&nbsp; [[Modulation_Methods/Quadrature_Amplitude_Modulation|"Quadrature Amplitude Modulation"]].
+*The page&nbsp; [[Modulation_Methods/Quadrature_Amplitude_Modulation#Signal_waveforms_for_4.E2.80.93QAM|"Signal waveforms for 4–QAM"]]&nbsp; is helpful for completing this exercise.
+*The signal space allocation considered can be seen in &nbsp;[[Aufgaben:Exercise_4.10Z:_Signal_Space_Constellation_of_the_16-QAM|Exercise 4.10Z]].&nbsp; The color highlights also correspond.
+*From question &nbsp; '''(6)'''&nbsp; onwards,&nbsp; use the parameter values&nbsp;$g_0 = 1 \ \rm V$&nbsp; and &nbsp;$T = 1 \ \rm &micro; s$.
+*Energy values are to be given in &nbsp;$\rm V^2s$&nbsp;; like this,&nbsp; they refer to the reference resistance &nbsp;$R = 1 \ \rm \Omega$.
+===Questions===
 <quiz display=simple>
-{Wie lautet der Amplitudenkoeffizient im roten Zeitintervall (0 < t < T)?
+{What are the real and imaginary part of the amplitude coefficient &nbsp;$a$&nbsp; in the red time interval &nbsp;$(0 < t < T)$?
 |type="{}"}
-$0 < t < T:   a_I$ = { 1 3% }
+$a_{\rm I} \ = \ $ { 1 3% }
-$a_Q$ = { 1 3% }
+$a_{\rm Q} \ = \ $ { 1 3% }
-{Welches Verhältnis besteht zwischen $s_0$ (maximale Hüllkurve des Sendesignals) und $g_0$ (maximale Hüllkurven der Teilsignale) ?
+{What is the relationship between &nbsp;$s_0$&nbsp; (maximum envelope of the transmitted signal) and &nbsp;$g_0$&nbsp; (maximum envelope of the partial signals)?
 |type="{}"}
-$s_0/g_0$ = { 1.414 3% }
+$s_0/g_0 \ = \ $ { 1.414 3% }
-{Wie lautet der Amplitudenkoeffizient im blauen Zeitintervall (T < t < 2T)?
+{What is the amplitude coefficient &nbsp;$a$&nbsp; in the blue time interval &nbsp;$(T < t < 2T)$?
 |type="{}"}
-$T < t < 2T:   a_I$ = { 0.333 3% }
+$a_{\rm I} \ = \ $ { 0.333 3% }
-$a_Q$ = { 0.333 3% }
+$a_{\rm Q} \ = \ $ { 0.333 3% }
-{Wie lautet der Amplitudenkoeffizient im grünen Zeitintervall (2T < t < 3T)? Ermitteln Sie auch dessen Betrag und die Phasenlage.
+{What is the amplitude coefficient &nbsp;$a$&nbsp; in the green time interval &nbsp;$(2T < t < 3T)$?&nbsp; Determine also its magnitude and phase.
 |type="{}"}
-$2T < t < 3T:   a_I$  = { -1 3% }
+$a_{\rm I} \ = \ $ { -1.03--0.97 }
-$a_Q$ = { 0.333 3% }
+$a_{\rm Q} \ = \ $ { 0.333 3% }
-{Wie lautet der Amplitudenkoeffizient im violetten Zeitintervall (3T < t < 4T)?
+{What is the amplitude coefficient &nbsp;$a$&nbsp; in the purple time interval  &nbsp;$(3T < t < 4T)$?
 |type="{}"}
-$ 3T < t < 4T:   a_I$ = { -0.1 3% }
+$a_{\rm I} \ = \ $ { -1.03--0.97 }
-$a_Q$ = { -0.333 3% }
+$a_{\rm Q} \ = \ $ { -0.343--0.323 }
-{Welche maximale Energie $E_{S, max}$ wird pro Symbol aufgewendet? Unter welcher Voraussetzung ist die mittlere Energie pro Symbol gleich $E_{S, max}$?
+{What is the maximum energy &nbsp;$E_\text{S, max}$&nbsp; expended per symbol?  Under what condition is the average energy per symbol equal to&nbsp;$E_\text{S, max}$?
 |type="{}"}
-$E_{S, max}$ = { 1 3% } $10^{-6}$ $V^2 s$
+$E_\text{S, max} \ = \ $ { 1 3% } $\ \cdot 10^{-6} \ \rm V^2 s$
-{Wie groß ist die maximale Energie pro Bit?
+{What is the maximum energy &nbsp;$E_\text{B, max}$&nbsp; per bit?
 |type="{}"}
-$E_{B, max}$ = {0.25 3% } $10^{-6}$ $V^2 s$
+$E_\text{B, max} \ = \ $ { 0.25 3% } $\ \cdot 10^{-6} \ \rm V^2 s$
-{Wie groß ist die minimale Energie $E_{B, min}$ pro Bit?
+{What is the minimum energy &nbsp;$E_\text{B, min}$&nbsp; per bit?
 |type="{}"}
-$E_{B, min}$ = { 0.28 3% } $10^{-7}$ $V^2 s$
+$E_\text{B, min} \ = \ $ { 0.028 3% } $\ \cdot 10^{-6} \ \rm V^2 s$
 </quiz>
-===Musterlösung===
+===Solution===
 {{ML-Kopf}}
-'''1.''' Aus dem (roten) Inphasesignal folgt (links entsprechend Definition, rechts gemäß Skizze):
+'''(1)'''&nbsp; From the&nbsp; (red)&nbsp; inphase signal  &nbsp; &rArr; &nbsp; the real part follows&nbsp; (first equation according to the definition,&nbsp; second equation according to the graph):
-$$ s_{\rm cos}(t)= a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)= g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm I}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$
+:$$ s_{\rm cos}(t)= a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)= g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm I}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$
-Entsprechend erkennt man aus dem Quadratursignal:
+*Accordingly,&nbsp; we recognize from the quadrature signal &nbsp; ⇒ &nbsp; imaginary part:
-$$ s_{\rm -sin}(t)= -a_{\rm Q}\cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)= -g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm Q}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$
+:$$ s_{\rm -sin}(t)= -a_{\rm Q}\cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)= -g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm Q}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$
+'''(2)'''&nbsp; The two partial signals each have the&nbsp; (maximum)&nbsp; envelope&nbsp; $g_0$,&nbsp; while &nbsp;$s_0$&nbsp;characterizes the transmitted signal&nbsp; $s(t)$.
+*As can be seen from the signal space allocation&nbsp; (see Exercise 4.10Z)&nbsp;:
+:$${s_0}/{ g_0 }= \sqrt{2}\hspace{0.15cm}\underline { = 1.414} \hspace{0.05cm}.$$
+'''(3)'''&nbsp; The amplitude coefficients&nbsp; $a_{\rm I}$&nbsp; and&nbsp; $a_{\rm Q}$&nbsp; have the same signs as in subtask&nbsp; '''(1)''',&nbsp; but with smaller magnitude:
+:$$a_{\rm I} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$
+'''(4)'''&nbsp;  In the third&nbsp; (green)&nbsp; interval,&nbsp; we can see a minus-cosine signal with amplitude&nbsp; $g_0$&nbsp; and a minus-sine signal with amplitude&nbsp; $g_0/3$:
+:$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$
+*As is yet to be calculated in sub-task&nbsp; '''(4)'''&nbsp; of Exercise 4.10Z,&nbsp; here the magnitude is equal to&nbsp; $|a| =1.054$&nbsp; and the phase angle is &nbsp; ${\rm arc} \ a \approx 161^\circ$.
+'''(5)'''&nbsp; The violet signal does not differ from the green interval in the in-phase component except in the sign of the quadrature component:
+:$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = - 1/3\hspace{0.15cm}\underline {= -0.333} \hspace{0.05cm}.$$
+'''(6)'''&nbsp; The maximum signal energy occurs when one of the four outer vertices is occupied. In that case:
+:$$ E_{\rm S, \hspace{0.05cm}max} = {1}/{2}\cdot s_0^2 \cdot T = {1}/{2}\cdot \left (\sqrt{2} \cdot g_0 \right )^2 \cdot T = g_0^2 \cdot T = (1\,{\rm V})^2 \cdot (1\,{\rm \mu s}) \hspace{0.15cm}\underline {= 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
+*The average signal energy is equal to the maximum value when only the corner points of the signal space mapping are occupied and the&nbsp; "inner symbols"&nbsp; are excluded from the encoding.
-'''2.''' Die beiden Teilsignale haben jeweils die (maximale) Hüllkurve $g_0$, während $s_0$ das Sendesignal $s(t)$ charakterisiert. Wie aus der Signalraumzuordnung (siehe Aufgabe Z4.9) hervorgeht, gilt
-$${s_0}/{ g_0 }= \sqrt{2}\hspace{0.15cm}\underline { = 1.414} \hspace{0.05cm}.$$
-'''3.'''  Die Amplitudenkoeffizienten aI und $a_Q$ haben die gleichen Vorzeichen wie bei der Teilaufgabe a), aber mit kleinerem Betrag: $a_I = a_Q = +1/3$.
-'''4.'''  Im dritten (grünen) Intervall erkennt man ein Minus–Cosinus–Signal mit der Amplitude $g_0$ und ein Minus–Sinus–Signal mit Amplitude $g_0/3$ ⇒ $a_I = –1$, $a_Q = +1/3$. Wie in Aufgabe Z4.9, Teilaufgabe d) noch berechnet werden soll, ist der Betrag gleich 1.054 und der Phasenwinkel etwa 161°.
+'''(7)'''&nbsp; Four bits are transmitted per symbol.&nbsp; From this it follows that:
+:$$ E_{\rm B, \hspace{0.05cm}max} = {E_{\rm S, \hspace{0.05cm}max}}/{4}\hspace{0.15cm}\underline {= 0.25 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
-'''5.'''   Das violette Signal unterscheidet sich vom grünen Intervall nicht in der Inphasekomponente, sondern nur im Vorzeichen der Quadraturkomponente ⇒ $a_I = –1$, $a_Q = –1/3$.
-'''6.''' Die maximale Signalenergie tritt auf, wenn einer der vier äußeren Eckpunkte belegt ist. Dann gilt:
-$$ E_{\rm S, \hspace{0.05cm}max} = \frac{1}{2}\cdot s_0^2 \cdot T = \frac{1}{2}\cdot \left (\sqrt{2} \cdot g_0 \right )^2 \cdot T = g_0^2 \cdot T = (1\,{\rm V})^2 \cdot (1\,{\rm \mu s}) \hspace{0.15cm}\underline {= 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
-Die mittlere Signalenergie ist gleich dem Maximalwert, wenn nur die Eckpunkte der Signalraumzuordnung belegt sind und „innere Symbole” von der Codierung ausgeschlossen werden.
-'''7.''' Pro Symbol werden vier Bit übertragen. Daraus folgt:
+'''(8)'''&nbsp;  The minimum signal energy is obtained at one of the inner signal space points and is smaller by a factor of $9$&nbsp; than in subtask&nbsp; '''(7)''':
-$$ E_{\rm B, \hspace{0.05cm}max} = \frac{E_{\rm S, \hspace{0.05cm}max}}{4}\hspace{0.15cm}\underline {= 0.25 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
+:$$E_{\rm B, \hspace{0.05cm}min} = \frac{E_{\rm B, \hspace{0.05cm}max}}{9} = \frac{g_0^2 \cdot T}{36} \hspace{0.15cm}\underline { \approx 0.028 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
-'''8.''' Die minimale Signalenergie ergibt sich bei einem der inneren Signalraumpunkte und ist gegenüber der letzten Teilaufgabe um den Faktor 9 kleiner:
+*In the theory section,&nbsp; it was shown that,&nbsp; assuming all symbols are equally likely,&nbsp; the average signal energy per bit for 16-QAM is approximately:
-$$E_{\rm B, \hspace{0.05cm}min} = \frac{E_{\rm B, \hspace{0.05cm}max}}{9} = \frac{g_0^2 \cdot T}{36} \hspace{0.15cm}\underline { \approx 0.28 \cdot 10^{-7}\,{\rm V^2s}}\hspace{0.05cm}.$$
+:$$E_{\rm B} \approx 0.139 · g_0^2 \cdot T = 0.035 \cdot 10^{-6}\,{\rm V^2s}.$$
-Im Theorieteil wird gezeigt, dass bei der 16–QAM die mittlere Signalenergie $E_B$ pro Bit unter der Voraussetzung, dass alle Symbole gleichwahrscheinlich sind, etwa $0.139 · g_0^2T$ ist.
 {{ML-Fuß}}
-[[Category:Aufgaben zu Modulationsverfahren|^4.3 Quadratur–Amplitudenmodulation^]]
+[[Category:Modulation Methods: Exercises|^4.3 Quadrature Amplitude Modulation^]]