Difference between revisions of "Aufgaben:Exercise 4.10Z: Correlation Duration"
From LNTwww
| (2 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID393__Sto_Z_4_10.png|right|frame| | + | [[File:P_ID393__Sto_Z_4_10.png|right|frame|Pattern signals of ergodic processes]] |
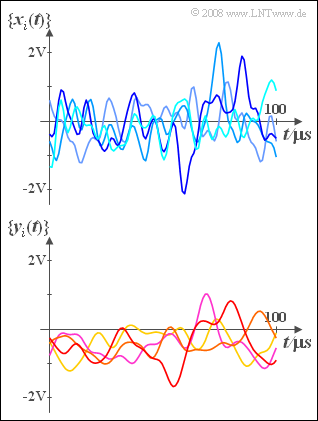
| − | The | + | The graphic shows pattern signals of two random processes $\{x_i(t)\}$ and $\{y_i(t)\}$ with equal power |
| + | :$$P_x = P_y = 5\hspace{0.05 cm} \rm mW.$$ | ||
| + | Assuming here the resistance $R = 50\hspace{0.05 cm}\rm \Omega$. | ||
| Line 13: | Line 15: | ||
| − | + | As can be seen from the diagram below, the random process $\{y_i(t)\}$ has much stronger internal statistical bindings than the random process $\{x_i(t)\}$. | |
| − | + | Or, to put it another way: | |
| − | As can be seen from the | ||
| − | Or, to put it another way: | ||
*The random process $\{y_i(t)\}$ is lower frequency than $\{x_i(t)\}$. | *The random process $\{y_i(t)\}$ is lower frequency than $\{x_i(t)\}$. | ||
*The equivalent ACF duration is $\nabla \tau_y = 10 \hspace{0.05 cm}\rm µ s $. | *The equivalent ACF duration is $\nabla \tau_y = 10 \hspace{0.05 cm}\rm µ s $. | ||
| Line 23: | Line 23: | ||
| − | From the sketch it can also be seen that $\{y_i(t)\}$ in contrast to $\{x_i(t)\}$ is not | + | From the sketch it can also be seen that $\{y_i(t)\}$ in contrast to $\{x_i(t)\}$ is not DC free. The DC signal component is rather $m_y = -0.3 \hspace{0.05 cm}\rm V$. |
| − | |||
| − | |||
| − | |||
| Line 32: | Line 29: | ||
| − | Hint: | + | '''Hint''': |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-Correlation Function]]. |
| − | *Reference is made in particular to the | + | *Reference is made in particular to the section [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Interpretation_of_the_auto-correlation_function|Interpretation of the auto-correlation function]]. |
| Line 48: | Line 45: | ||
| − | {What ACF | + | {What ACF values result for $\tau = 2\hspace{0.05 cm}\rm µs$ resp. $\tau = 5\hspace{0.05 cm}\rm µ s$? |
|type="{}"} | |type="{}"} | ||
$\varphi_x(\tau = 2\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 3.025 3% } $\ \rm mW$ | $\varphi_x(\tau = 2\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 3.025 3% } $\ \rm mW$ | ||
| Line 54: | Line 51: | ||
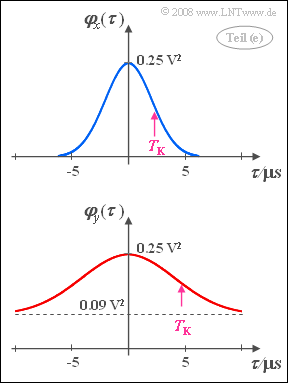
| − | {What is the correlation time $T_{\rm K}$, i.e. the time at which the ACF has dropped to half of the maximum? | + | {What is the correlation time $T_{\rm K}$, i.e. the time at which the ACF has dropped to half of the maximum? |
|type="{}"} | |type="{}"} | ||
$T_{\rm K} \ = \ $ { 2.35 3% } $\ \rm µ s$ | $T_{\rm K} \ = \ $ { 2.35 3% } $\ \rm µ s$ | ||
| Line 64: | Line 61: | ||
| − | {Calculate the ACF $\varphi_x(\tau)$. What is the ACF value at $\tau = 10\hspace{0.05 cm}\rm µ s$? What would be the ACF | + | {Calculate the ACF $\varphi_x(\tau)$. What is the ACF value at $\tau = 10\hspace{0.05 cm}\rm µ s$? What would be the ACF curve with positive mean $(m_y = +0.3 \hspace{0.05 cm}\rm V)$? |
|type="{}"} | |type="{}"} | ||
$\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 1.938 3% } $\ \rm mW$ | $\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 1.938 3% } $\ \rm mW$ | ||
| Line 74: | Line 71: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The | + | '''(1)''' The second moment results to $m_{2x} = R \cdot P_x = 50 \hspace{0.05 cm}{\rm \Omega}\cdot 5 \hspace{0.05 cm}{\rm mW}= 0.25 \hspace{0.05 cm}{\rm V}^2.$ |
*From this follows the standard deviation $\sigma_x\hspace{0.15 cm}\underline{= 0.5\hspace{0.05 cm}{\rm V}}$. | *From this follows the standard deviation $\sigma_x\hspace{0.15 cm}\underline{= 0.5\hspace{0.05 cm}{\rm V}}$. | ||
| − | '''(2)''' Because $P_x = \varphi_x (\tau = 0)$ holds for the ACF in general: | + | '''(2)''' Because of $P_x = \varphi_x (\tau = 0)$ holds for the ACF in general: |
:$$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$ | :$$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$ | ||
*From this we obtain: | *From this we obtain: | ||
| Line 92: | Line 89: | ||
*From this follows $T_{\rm K}\hspace{0.15 cm}\underline{= 2.35\hspace{0.05 cm}{\rm µ s}}$. | *From this follows $T_{\rm K}\hspace{0.15 cm}\underline{= 2.35\hspace{0.05 cm}{\rm µ s}}$. | ||
| − | *With | + | *With another ACF form, a different ratio is obtained for $T_{\rm K} / {\rm \nabla} \tau_x$. |
| − | '''(4)''' Because $P_x = P_y$ the | + | '''(4)''' Because of $P_x = P_y$ the second order moments of $x$ and $y$ are equal $0.25\hspace{0.05 cm}\rm V^2$. |
*Taking into account the mean value $m_y = -0.3 \hspace{0.05 cm}\rm V$ holds: | *Taking into account the mean value $m_y = -0.3 \hspace{0.05 cm}\rm V$ holds: | ||
:$$m_y^2 + \sigma_y^2 = \rm 0.25 \hspace{0.05 cm} V^2.$$ | :$$m_y^2 + \sigma_y^2 = \rm 0.25 \hspace{0.05 cm} V^2.$$ | ||
| Line 105: | Line 102: | ||
| − | '''(5)''' In terms of unit resistance $ R = 1 \hspace{0.05 cm}{\rm \Omega}$ the | + | '''(5)''' In terms of unit resistance $ R = 1 \hspace{0.05 cm}{\rm \Omega}$ the ACF of the process $\{y_i(t)\}$ is: |
:$$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$ | :$$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$ | ||
| − | *On the right you can see the | + | *On the right you can see the ACF curve. Related to the resistor $ R = 50 \hspace{0.05 cm}{\rm \Omega}$ results in the following ACF values: |
:$$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.5cm} \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$ | :$$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.5cm} \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$ | ||
| Line 115: | Line 112: | ||
\hspace{0.15 cm}\underline{=1.938\hspace{0.05 cm}\rm mW}.$$ | \hspace{0.15 cm}\underline{=1.938\hspace{0.05 cm}\rm mW}.$$ | ||
| − | *With positive mean $m_y$ (having the same | + | *With positive mean $m_y$ $($having the same magnitude$)$, there would be no change in the ACF, since $m_y$ is squared in the ACF equation. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 19:52, 20 March 2022
Pattern signals of ergodic processes
The graphic shows pattern signals of two random processes $\{x_i(t)\}$ and $\{y_i(t)\}$ with equal power
- $$P_x = P_y = 5\hspace{0.05 cm} \rm mW.$$
Assuming here the resistance $R = 50\hspace{0.05 cm}\rm \Omega$.
The random process $\{x_i(t)\}$
- is zero mean $(m_x = 0)$,
- has the Gaussian ACF $\varphi_x (\tau) = \varphi_x (\tau = 0) \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2},$ and
- exhibits the equivalent ACF duration $\nabla \tau_x = 5\hspace{0.05 cm}\rm µ s $ .
As can be seen from the diagram below, the random process $\{y_i(t)\}$ has much stronger internal statistical bindings than the random process $\{x_i(t)\}$.
Or, to put it another way:
- The random process $\{y_i(t)\}$ is lower frequency than $\{x_i(t)\}$.
- The equivalent ACF duration is $\nabla \tau_y = 10 \hspace{0.05 cm}\rm µ s $.
From the sketch it can also be seen that $\{y_i(t)\}$ in contrast to $\{x_i(t)\}$ is not DC free. The DC signal component is rather $m_y = -0.3 \hspace{0.05 cm}\rm V$.
Hint:
- The exercise belongs to the chapter Auto-Correlation Function.
- Reference is made in particular to the section Interpretation of the auto-correlation function.
Questions
Solution
(1) The second moment results to $m_{2x} = R \cdot P_x = 50 \hspace{0.05 cm}{\rm \Omega}\cdot 5 \hspace{0.05 cm}{\rm mW}= 0.25 \hspace{0.05 cm}{\rm V}^2.$
- From this follows the standard deviation $\sigma_x\hspace{0.15 cm}\underline{= 0.5\hspace{0.05 cm}{\rm V}}$.
(2) Because of $P_x = \varphi_x (\tau = 0)$ holds for the ACF in general:
- $$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$
- From this we obtain:
- $$\varphi_x (\tau = {\rm 2\hspace{0.1cm} µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- {\rm 0.16 }\pi } \hspace{0.15cm}\underline{= 3.025 \hspace{0.1cm} \rm mW},$$
- $$\varphi_x (\tau = {\rm 5\hspace{0.1cm} \rm µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi } \hspace{0.15cm}\underline{= 0.216 \hspace{0.1cm} \rm mW}.$$
Two times Gaussian ACF
(3) Here the following determination equation holds:
- $${\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(T_{\rm K} / {\rm \nabla} \tau_x)^2} \stackrel{!}{=} {\rm 0.5} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} (T_{\rm K} / {\rm \nabla} \tau_x)^2 = \sqrt{{ \ln(2)}/{\pi}}\hspace{0.05cm}.$$
- From this follows $T_{\rm K}\hspace{0.15 cm}\underline{= 2.35\hspace{0.05 cm}{\rm µ s}}$.
- With another ACF form, a different ratio is obtained for $T_{\rm K} / {\rm \nabla} \tau_x$.
(4) Because of $P_x = P_y$ the second order moments of $x$ and $y$ are equal $0.25\hspace{0.05 cm}\rm V^2$.
- Taking into account the mean value $m_y = -0.3 \hspace{0.05 cm}\rm V$ holds:
- $$m_y^2 + \sigma_y^2 = \rm 0.25 \hspace{0.05 cm} V^2.$$
- From this follows:
- $$\sigma_y\hspace{0.15 cm}\underline{= 0.4\hspace{0.05 cm}{\rm V}}.$$
(5) In terms of unit resistance $ R = 1 \hspace{0.05 cm}{\rm \Omega}$ the ACF of the process $\{y_i(t)\}$ is:
- $$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$
- On the right you can see the ACF curve. Related to the resistor $ R = 50 \hspace{0.05 cm}{\rm \Omega}$ results in the following ACF values:
- $$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.5cm} \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$
- From this follows:
- $$\varphi_y(\tau) = 1.8 \hspace{0.1cm} {\rm mW} + 3.2 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2} \hspace{0.3cm }\Rightarrow \hspace{0.3cm }\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \hspace{0.15 cm}\underline{=1.938\hspace{0.05 cm}\rm mW}.$$
- With positive mean $m_y$ $($having the same magnitude$)$, there would be no change in the ACF, since $m_y$ is squared in the ACF equation.
