Aufgaben:Exercise 4.10Z: Signal Space Constellation of the 16-QAM

• Return to book

Signalraumkonstellation

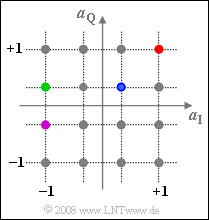
We now consider the 16-QAM method according to the block diagram given in the theory section. The diagram shows the possible complex amplitude coefficients  $a = a_{\rm I} + {\rm j} · a_{\rm Q}$.

As in Exercise 4.10 , the following should be assumed:

• The possible amplitude coefficients  $a_{\rm I}$  and  $a_{\rm Q}$  of the two component signals are $ ±1$  and  $±1/3$, respectively.
• The fundamental transmission pulse  $g_s(t)$  is rectangular with amplitude  $g_0 = 1\ \rm V$  and duration  $T = 1 \ \rm µ s$.
• The source signal  $q(t)$  before the serial-to-parallel converter is binary and redundancy-free.

Hints:

• This exercise belongs to the chapter   Quadrature Amplitude Modulation.
• Zur Lösung der Aufgabe ist die Seite  Quadratic QAM signal space constellations hilfreich.
• The signals belonging to the colored points are shown in the same colors as in Exercise 4.10.

Questions

1

Wie groß ist die Bitrate  $R_{\rm B}$  des binären Quellensymbols  $q(t)$?

$R_{\rm B}\ = \ $ $\ \rm Mbit/s$

2

Geben Sie den Betrag und die Phase  $($zwischen  $±180^\circ)$  für das rote Symbol an   ⇒   $a = 1 +{\rm j}$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm Grad$

3

Geben Sie den Betrag und die Phase für das blaue Symbol an   ⇒   $a = 1/3 +{\rm j}/3$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm Grad$

4

Geben Sie den Betrag und die Phase für das grüne Symbol an   ⇒   $a = -1 +{\rm j}/3$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm Grad$

5

Geben Sie den Betrag und die Phase für das violette Symbol an   ⇒   $a = -1 -{\rm j}/3$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm Grad$

6

Wieviele unterschiedliche Beträge   ⇒   $N_{|a|}$  und Phasenlagen   ⇒   $N_{arc}$ sind möglich?

$N_{|a|}\ = \ $

$N_{\rm arc}\ = \ $

Musterlösung

Solution

(1)  Durch ein Symbol werden jeweils  $\log_2 \ 16 = 4$  Bit des Quellensignals dargestellt, zwei Bit durch den vierstufigen Koeffizienten  $a_{\rm I}$  und zwei weitere durch  $a_{\rm Q}$.

• Die Bitdauer beträgt somit  $T_{\rm B} = T/4 = 0.25 \ \rm µ s$.
• Damit ist die Bitrate  $R_{\rm B} = 1/T_{\rm B}\hspace{0.15cm}\underline { = 4 \ \rm Mbit/s}$.

(2)  Aus der Geometrie folgt für  $a = 1 + {\rm j}$:

$$a| = \sqrt{1^2 + 1^2}= \sqrt{2}\hspace{0.15cm}\underline { =1.414}\hspace{0.05cm}, \hspace{0.5cm} {\rm arc}\hspace{0.15cm} a = \arctan \left ({1}/{1} \right ) \hspace{0.15cm}\underline {= 45^{\circ}}\hspace{0.05cm}.$$

(3)  Der Winkel ergibt sich wie bei der Teilaufgabe  (2), der Betrag ist um den Faktor  $3$  kleiner:

$$|a| = \sqrt{(1/3)^2 + (1/3)^2}= \sqrt{2}\hspace{0.15cm}\underline { =0.471}\hspace{0.05cm}, \hspace{0.5cm} {\rm arc}\hspace{0.15cm} a \hspace{0.15cm}\underline {= 45^{\circ}}\hspace{0.05cm}.$$

(4)  Für den komplexen Amplitudenkoeffizienten  $a = -1 + {\rm j}/3$  erhält man aus der Geometrie:

$$|a| = \sqrt{1^2 + (1/3)^2}\hspace{0.15cm}\underline {= 1.054}\hspace{0.05cm},\hspace{0.5cm} {\rm arc}\hspace{0.15cm} a = 180^{\circ} - \arctan \left ( {1}/{3} \right ) = 180^{\circ} - 18.43^{\circ} \hspace{0.15cm}\underline {= 161.57^{\circ}}\hspace{0.05cm}.$$

(5)  Das violette Symbol  $a = -1 - {\rm j}/3$  hat den gleichen Betrag wie das grüne Symbol nach Teilaufgabe  (4), während der Phasenwinkel das Vorzeichen ändert:

$$|a| \hspace{0.15cm}\underline {= 1.054}\hspace{0.05cm},\hspace{0.5cm} {\rm arc}\hspace{0.15cm} a \hspace{0.15cm}\underline {= -161.57^{\circ}}\hspace{0.05cm}.$$

(6)  Für den Betrag sind  $N_{|a|}\hspace{0.15cm}\underline { = 3}$  verschiedene Ergebnisse möglich:  $1.414$,  $1.054$  und  $0.471$.

• Dagegen gibt es  $N_{\rm arc}\hspace{0.15cm}\underline { = 12}$  mögliche Phasenlagen, nämlich:

$$ \pm \arctan (1/3) = \pm 18.43^{\circ}, \hspace{0.2cm}\pm \arctan (1) = \pm 45^{\circ}, \hspace{0.2cm}\pm \arctan (3) = \pm 71.57^{\circ}\hspace{0.05cm},$$

$$\pm (180^{\circ}-71.57^{\circ}) = \pm 108.43^{\circ}, \hspace{0.2cm}\pm (180^{\circ}-45^{\circ}) = \pm 135^{\circ}, \hspace{0.2cm}\pm 161.57^{\circ} \hspace{0.05cm}.$$