Difference between revisions of "Aufgaben:Exercise 4.11: Analysis of Parity-check Matrices"
m (Guenter moved page Exercise 4.11: Analysis of Parity-Check Matrices to Exercise 4.11: Analysis of Parity-check Matrices) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes}} |
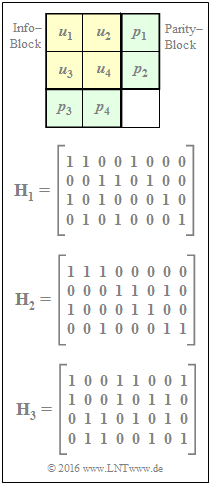
| − | [[File:P_ID3067__KC_A_4_11_v2.png|right|frame| | + | [[File:P_ID3067__KC_A_4_11_v2.png|right|frame|Product code described by the parity-check matrix $\mathbf{H}$]] |
| − | In | + | In the adjacent graphic, a product code is indicated at the top, which is characterized by the following parity-check equations: |
:$$p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_2\hspace{0.05cm},\hspace{0.3cm} | :$$p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_2\hspace{0.05cm},\hspace{0.3cm} | ||
p_2 = u_3 \oplus u_4\hspace{0.05cm},\hspace{0.3cm} | p_2 = u_3 \oplus u_4\hspace{0.05cm},\hspace{0.3cm} | ||
| Line 8: | Line 8: | ||
p_4 = u_2 \oplus u_4\hspace{0.05cm}.$$ | p_4 = u_2 \oplus u_4\hspace{0.05cm}.$$ | ||
| − | + | Below are given the check matrices $\mathbf{H}_1, \ \mathbf{H}_2$ and $\mathbf{H}_3$ . To be checked is which of the matrices has the given product code according to the equation $\underline{x} = \underline{u} \cdot \mathbf{H}^{\rm T}$ correctly describing the given product code, assuming the following definitions: | |
| − | * | + | * the code word $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$, |
| − | * | + | * the code word $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$. |
| − | + | All $\mathbf{H}$–matrices contain fewer ones than zeros. This is a characteristic of the so-called low–density parity–check codes (short: $\rm LDPC$ codes). In the case of LDPC codes relevant to practice, however, the share of ones is still significantly lower than in these examples. | |
| − | + | Furthermore, note for the exercise: | |
| − | * | + | * A $(n, \ k)$–block code is systematic if the first $k$ bits of the code word $\underline{x}$ contains the information word $\underline{u}$ . With the code word definition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$ the parity-check matrix $\mathbf{H}$ must then end with a $k × k$ diagonal matrix. |
| − | * | + | * A <i>regular code</i> (with respect to LDPC application) exists, if the Hamming–weight of all rows ⇒ $w_{\rm Z}$ and the Hamming weight of all columns ⇒ $w_{\rm S}$ are equal in each case. Otherwise, one speaks of an <i>irregular LDPC code</i>. |
| − | * | + | * The parity-check matrix $\mathbf{H}$ of a conventional linear $(n, \ k)$ block code consists of exactly $m = n - k$ rows and $n$ columns. For LDPC codes, on the other hand, the requirement is $m ≥ n - k$. The equal sign is true if the $m$ parity-check equations are statistically independent. |
| − | * | + | * From the parity-check matrix $\mathbf{H}$ a lower bound for the code rate $R$ can be given: |
:$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} | :$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} | ||
\hspace{0.5cm}{\rm mit}\hspace{0.5cm} | \hspace{0.5cm}{\rm mit}\hspace{0.5cm} | ||
| Line 27: | Line 27: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *This equation applies equally to regular and irregular LDPC–codes, where the regular codes ${\rm E}[w_{\rm S}] = w_{\rm S}$ and ${\rm E}[w_{\rm Z}] = w_{\rm Z}$ can be considered. |
| Line 37: | Line 37: | ||
| − | + | Hints: | |
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes|"Basics of the Low–density Parity–check"]]. |
| − | * | + | * Reference is made in particular to the page [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Some_characteristics_of_LDPC_codes|"Some characteristics of LDPC codes"]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which parity-check matrix describes the given product code according to the sketch above? |
|type="[]"} | |type="[]"} | ||
| − | + $\mathbf{H}_1$ | + | + $\mathbf{H}_1$ given $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$. |
| − | - $\mathbf{H}_1$ | + | - $\mathbf{H}_1$ given $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$. |
| − | + $\mathbf{H}_2$ | + | + $\mathbf{H}_2$ given $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$. |
| − | - $\mathbf{H}_3$ | + | - $\mathbf{H}_3$ given $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$. |
| − | { | + | {For the remaining subtasks we shall always assume $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$. <br>Which statements are valid for the parity-check matrix $\mathbf{H}_1$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The code is systematic. |
| − | - | + | - The code is regular. |
| − | - | + | - For the code rate holds $R > 1/2$. |
| − | + | + | + For the code rate holds $R = 1/2$. |
| − | { | + | {What statements hold for the parity-check matrix $\mathbf{H}_3$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - No relation between $\mathbf{H}_1$ and $\mathbf{H}_3$ is discernible. |
| − | + | + | + The $\mathbf{H}_3$–rows are linear combinations of two $\mathbf{H}_1$ ;rows each. |
| − | + | + | + The four parity-check equations according to $\mathbf{H}_3$ are linearly independent. |
| − | { | + | {Which statements apply to the code denoted by $\mathbf{H}_3$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The code is systematic. |
| − | + | + | + The code is regular. |
| − | + | + | + For the code rate holds $R ≥ 1/2$. |
| − | + | + | + For the code rate holds $R = 1/2$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>solutions 1 and 3</u>: |
| − | * | + | *With the code word definition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$, the parity-check matrix $\mathbf{H}_1$ denotes the following check equations: |
:$$u_1 \oplus u_2 \oplus p_1 = 0\hspace{0.05cm},\hspace{0.3cm} | :$$u_1 \oplus u_2 \oplus p_1 = 0\hspace{0.05cm},\hspace{0.3cm} | ||
u_3 \oplus u_4 \oplus p_2 = 0\hspace{0.05cm},\hspace{0.3cm} | u_3 \oplus u_4 \oplus p_2 = 0\hspace{0.05cm},\hspace{0.3cm} | ||
u_1 \oplus u_3 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} | u_1 \oplus u_3 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} | ||
u_2 \oplus u_4 \oplus p_4 = 0\hspace{0.05cm}.$$ | u_2 \oplus u_4 \oplus p_4 = 0\hspace{0.05cm}.$$ | ||
| − | * | + | *This corresponds exactly to the assumptions made above. The same result is obtained for $\mathbf{H}_2$ and the code word definition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$. |
| − | + | With the same code word definition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$ the other parity-check matrices do not yield a meaningful set of equations: | |
| − | * | + | * According to parity-check matrix $\mathbf{H}_1$: |
:$$u_1 \oplus p_1 \oplus u_3 = 0\hspace{0.05cm},\hspace{0.3cm} | :$$u_1 \oplus p_1 \oplus u_3 = 0\hspace{0.05cm},\hspace{0.3cm} | ||
u_2 \oplus p_2 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} | u_2 \oplus p_2 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} | ||
u_1 \oplus u_2 \oplus u_4 = 0\hspace{0.05cm},\hspace{0.3cm} | u_1 \oplus u_2 \oplus u_4 = 0\hspace{0.05cm},\hspace{0.3cm} | ||
p_1 \oplus p_2 \oplus p_4 = 0\hspace{0.05cm};$$ | p_1 \oplus p_2 \oplus p_4 = 0\hspace{0.05cm};$$ | ||
| − | * | + | * corresponding to parity-check matrix $\mathbf{H}_3$: |
:$$u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} | :$$u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} | ||
u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} | u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} | ||
| Line 97: | Line 97: | ||
| − | '''(2)''' | + | '''(2)''' Correct are the <u>proposed solutions 1 and 4</u>: |
| − | * | + | * The code is systematic because $\mathbf{H}_1$ ends with a $4 × 4$ diagonal matrix. |
| − | * | + | *For a regular (LDPC) code, there should be an equal number of ones in each row and in each column. |
| − | * | + | *The first condition is satisfied $(w_{\rm Z} = 3)$, but not the second. Rather, there is (equally often) one one or two ones per column ⇒ ${\rm E}[w_{\rm S}] = 1.5$. |
| − | * | + | * For an irregular code, the lower bound for the code rate is: |
:$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} | :$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} | ||
= 1 - \frac{1.5}{3} = 1/2 | = 1 - \frac{1.5}{3} = 1/2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * Because of the given code structure ($k = 4$ information bits, $m = 4$ check bits ⇒ $n = 8$ code bits) the code rate can also be given in the conventional form: $R = k/n$ ⇒ Correct is solution 4 in contrast to answer 3. |
| − | '''(3)''' | + | '''(3)''' The $\mathbf{H}_3$–rows result from linear combinations of $\mathbf{H}_1$–rows: |
| − | * | + | * The first $\mathbf{H}_3$–row is the sum of row 1 and row 4. |
| − | * | + | * The second $\mathbf{H}_3$–row is the sum of row 2 and row 3. |
| − | * | + | * The third $\mathbf{H}_3$–row is the sum of row 1 and row 3. |
| − | * | + | * The fourth $\mathbf{H}_3$–row is the sum of row 2 and row 4. |
| − | + | By linear combinations, the four linearly independent equations with respect to $\mathbf{H}_1$ now become four linearly independent equations with respect to $\mathbf{H}_3$ <br>⇒ Therefore, the <u>proposed solutions 2 and 3</u> are correct. | |
| − | '''(4)''' | + | '''(4)''' Here, <u>solutions 2, 3, and 4</u> are correct: |
| − | * | + | * If the code described by $\mathbf{H}_3$ were systematic, $\mathbf{H}_3$ should end with a $4 × 4$–diagonal matrix. This is not the case here. |
| − | * | + | * The Hamming weights of all rows are equal $(w_{\rm Z} = 4)$ and also all columns each have the same Hamming weight $(w_{\rm S} = 2)$ ⇒ the code is regular. |
| − | * | + | * This gives $R ≥ 1 - 2/4 = 1/2$ for the code rate. But since the four rows of $\mathbf{H}_3$ also describe four independent equations, the equal sign ⇒ $R = 1/2$ also holds. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:09, 10 December 2022
In the adjacent graphic, a product code is indicated at the top, which is characterized by the following parity-check equations:
- $$p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_2\hspace{0.05cm},\hspace{0.3cm} p_2 = u_3 \oplus u_4\hspace{0.05cm},\hspace{0.3cm} p_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_3\hspace{0.05cm},\hspace{0.3cm} p_4 = u_2 \oplus u_4\hspace{0.05cm}.$$
Below are given the check matrices $\mathbf{H}_1, \ \mathbf{H}_2$ and $\mathbf{H}_3$ . To be checked is which of the matrices has the given product code according to the equation $\underline{x} = \underline{u} \cdot \mathbf{H}^{\rm T}$ correctly describing the given product code, assuming the following definitions:
- the code word $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$,
- the code word $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.
All $\mathbf{H}$–matrices contain fewer ones than zeros. This is a characteristic of the so-called low–density parity–check codes (short: $\rm LDPC$ codes). In the case of LDPC codes relevant to practice, however, the share of ones is still significantly lower than in these examples.
Furthermore, note for the exercise:
- A $(n, \ k)$–block code is systematic if the first $k$ bits of the code word $\underline{x}$ contains the information word $\underline{u}$ . With the code word definition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$ the parity-check matrix $\mathbf{H}$ must then end with a $k × k$ diagonal matrix.
- A regular code (with respect to LDPC application) exists, if the Hamming–weight of all rows ⇒ $w_{\rm Z}$ and the Hamming weight of all columns ⇒ $w_{\rm S}$ are equal in each case. Otherwise, one speaks of an irregular LDPC code.
- The parity-check matrix $\mathbf{H}$ of a conventional linear $(n, \ k)$ block code consists of exactly $m = n - k$ rows and $n$ columns. For LDPC codes, on the other hand, the requirement is $m ≥ n - k$. The equal sign is true if the $m$ parity-check equations are statistically independent.
- From the parity-check matrix $\mathbf{H}$ a lower bound for the code rate $R$ can be given:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm S}(i) \hspace{0.5cm}{\rm und}\hspace{0.5cm} {\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm Z}(j) \hspace{0.05cm}.$$
- This equation applies equally to regular and irregular LDPC–codes, where the regular codes ${\rm E}[w_{\rm S}] = w_{\rm S}$ and ${\rm E}[w_{\rm Z}] = w_{\rm Z}$ can be considered.
Hints:
- This exercise belongs to the chapter "Basics of the Low–density Parity–check".
- Reference is made in particular to the page "Some characteristics of LDPC codes".
Questions
Solution
- With the code word definition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$, the parity-check matrix $\mathbf{H}_1$ denotes the following check equations:
- $$u_1 \oplus u_2 \oplus p_1 = 0\hspace{0.05cm},\hspace{0.3cm} u_3 \oplus u_4 \oplus p_2 = 0\hspace{0.05cm},\hspace{0.3cm} u_1 \oplus u_3 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_2 \oplus u_4 \oplus p_4 = 0\hspace{0.05cm}.$$
- This corresponds exactly to the assumptions made above. The same result is obtained for $\mathbf{H}_2$ and the code word definition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.
With the same code word definition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$ the other parity-check matrices do not yield a meaningful set of equations:
- According to parity-check matrix $\mathbf{H}_1$:
- $$u_1 \oplus p_1 \oplus u_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_2 \oplus p_2 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_1 \oplus u_2 \oplus u_4 = 0\hspace{0.05cm},\hspace{0.3cm} p_1 \oplus p_2 \oplus p_4 = 0\hspace{0.05cm};$$
- corresponding to parity-check matrix $\mathbf{H}_3$:
- $$u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} p_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} p_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm}.$$
(2) Correct are the proposed solutions 1 and 4:
- The code is systematic because $\mathbf{H}_1$ ends with a $4 × 4$ diagonal matrix.
- For a regular (LDPC) code, there should be an equal number of ones in each row and in each column.
- The first condition is satisfied $(w_{\rm Z} = 3)$, but not the second. Rather, there is (equally often) one one or two ones per column ⇒ ${\rm E}[w_{\rm S}] = 1.5$.
- For an irregular code, the lower bound for the code rate is:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} = 1 - \frac{1.5}{3} = 1/2 \hspace{0.05cm}.$$
- Because of the given code structure ($k = 4$ information bits, $m = 4$ check bits ⇒ $n = 8$ code bits) the code rate can also be given in the conventional form: $R = k/n$ ⇒ Correct is solution 4 in contrast to answer 3.
(3) The $\mathbf{H}_3$–rows result from linear combinations of $\mathbf{H}_1$–rows:
- The first $\mathbf{H}_3$–row is the sum of row 1 and row 4.
- The second $\mathbf{H}_3$–row is the sum of row 2 and row 3.
- The third $\mathbf{H}_3$–row is the sum of row 1 and row 3.
- The fourth $\mathbf{H}_3$–row is the sum of row 2 and row 4.
By linear combinations, the four linearly independent equations with respect to $\mathbf{H}_1$ now become four linearly independent equations with respect to $\mathbf{H}_3$
⇒ Therefore, the proposed solutions 2 and 3 are correct.
(4) Here, solutions 2, 3, and 4 are correct:
- If the code described by $\mathbf{H}_3$ were systematic, $\mathbf{H}_3$ should end with a $4 × 4$–diagonal matrix. This is not the case here.
- The Hamming weights of all rows are equal $(w_{\rm Z} = 4)$ and also all columns each have the same Hamming weight $(w_{\rm S} = 2)$ ⇒ the code is regular.
- This gives $R ≥ 1 - 2/4 = 1/2$ for the code rate. But since the four rows of $\mathbf{H}_3$ also describe four independent equations, the equal sign ⇒ $R = 1/2$ also holds.