Difference between revisions of "Aufgaben:Exercise 4.11Z: Code Rate from the Parity-check Matrix"
m (Guenter moved page Aufgabe 4.11Z: Coderate aus der Prüfmatrix to Exercise 4.11Z: Code Rate from the Parity-check Matrix) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes}} |
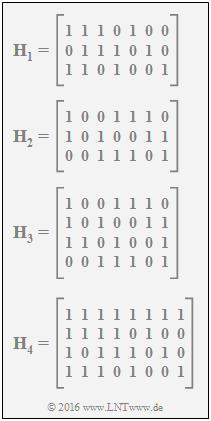
| − | [[File:P_ID3068__KC_Z_4_11_v4.png|right|frame| | + | [[File:P_ID3068__KC_Z_4_11_v4.png|right|frame|Given parity-check matrices]] |
| − | In | + | In this exercise, the code rates of the codes $\mathcal {C}_1, \, \mathcal {C}_2, \, \mathcal {C}_3$ and $\mathcal {C}_4$ are to be determined, where the codes are given by their test matrices alone. A lower bound on the code rate $R$ reads: |
:$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} | :$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | If the $m$ parity-check equations of all matrix–rows are linearly independent, then the equal sign in the above inequality holds. | |
| − | + | Used here is the following nomenclature: | |
| − | * $w_{\rm Z}(j)$ | + | * $w_{\rm Z}(j)$ with $1 ≤ j ≤ m$ being the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"Hamming weight"]] of $j$th row of the parity-check matrix. |
| − | * | + | * By <i>expectation value formation</i> results: |
:$${\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{m} | :$${\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{m} | ||
w_{\rm Z}(j)\hspace{0.05cm}.$$ | w_{\rm Z}(j)\hspace{0.05cm}.$$ | ||
| − | * | + | * Accordingly, $w_{\rm S}(i)$ with $1 ≤ i ≤ n$ gives the Hamming weight of $i$th column of $\mathbf{H}$ with expected value |
:$${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n} | :$${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n} | ||
w_{\rm S}(i)\hspace{0.05cm}.$$ | w_{\rm S}(i)\hspace{0.05cm}.$$ | ||
| Line 26: | Line 26: | ||
| − | + | Hints: | |
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes|"Basics of Low–density Parity–check Code "s]]. |
| − | * | + | * Reference is made in particular to the page [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Some_characteristics_of_LDPC_codes|"Some characteristics of LDPC codes"]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | {$\mathbf{H}_1$ | + | {$\mathbf{H}_1$ describes a systematic code. What are its parameters? |
|type="{}"} | |type="{}"} | ||
$n \hspace{0.27cm} = \ ${ 7 } | $n \hspace{0.27cm} = \ ${ 7 } | ||
| Line 41: | Line 41: | ||
$m \hspace{0.15cm} = \ ${ 3 } | $m \hspace{0.15cm} = \ ${ 3 } | ||
| − | { | + | {What is the code rate of the code $\mathcal {C}_1$ with the parity-check matrix $\mathbf{H}_1$? |
|type="{}"} | |type="{}"} | ||
$R \ = \ ${ 0.571 3% } | $R \ = \ ${ 0.571 3% } | ||
| − | { | + | {What is the code rate of the code $\mathcal {C}_1$ with the parity-check matrix $\mathbf{H}_2$? |
|type="{}"} | |type="{}"} | ||
$R \ = \ ${ 0.571 3% } | $R \ = \ ${ 0.571 3% } | ||
| − | { | + | {What is the code rate of the code $\mathcal {C}_1$ with the parity-check matrix $\mathbf{H}_3$? |
|type="{}"} | |type="{}"} | ||
$R \ = \ ${ 0.571 3% } | $R \ = \ ${ 0.571 3% } | ||
| − | { | + | {What is the code rate of the code $\mathcal {C}_1$ with the parity-check matrix $\mathbf{H}_4$? |
|type="{}"} | |type="{}"} | ||
$R \ = \ ${ 0.5 3% } | $R \ = \ ${ 0.5 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The matrix $\mathbf{H}_1$ ends with a $3 × 3$–diagonal matrix. |
| − | * | + | *This is the characteristic of a systematic code with $\underline{m = 3}$ parity-check equations. |
| − | * | + | *The code length is $\underline{n = 7}$. |
| − | * | + | *Thus, a codeword contains $\underline{k = 4}$ information bits. |
| − | <i> | + | <i>Note:</i> This is the [[Channel_Coding/General_Description_of_Linear_Block_Codes#Some_properties_of_the_.287.2C_4.2C_3.29_Hamming_code|"systematic (7, 4, 3)–Hamming code"]]. |
| − | '''(2)''' | + | '''(2)''' The code rate of the (7, 4, 3)–Hamming–code is $\underline{R = 4/7 = 0.571}$. |
| − | * | + | *The Hamming weight for all $m = 3$ rows is $w_{\rm Z} = 4$ and for the mean Hamming–weight over all columns holds: |
:$${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n} | :$${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n} | ||
w_{\rm S}(j) = 1/7 \cdot [2 + 3 + 2+2 + 1+1 +1] | w_{\rm S}(j) = 1/7 \cdot [2 + 3 + 2+2 + 1+1 +1] | ||
= 12/7 \hspace{0.05cm}.$$ | = 12/7 \hspace{0.05cm}.$$ | ||
| − | * | + | *This applies to the specified lower bound of the code rate: |
:$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{w_{\rm Z}} | :$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{w_{\rm Z}} | ||
= 1 - \frac{12/7}{4}\hspace{0.15cm} \underline{= 4/7 \approx 0.571}\hspace{0.05cm}.$$ | = 1 - \frac{12/7}{4}\hspace{0.15cm} \underline{= 4/7 \approx 0.571}\hspace{0.05cm}.$$ | ||
| − | * | + | *This means: the actual code rate is equal to the lower bound ⇒ the $m = 3$ parity-check equations of $\mathbf{H}_1$ are linearly independent. |
| − | '''(3)''' | + | '''(3)''' The first row of $\mathbf{H}_2$ is the sum of the first row $(z_1)$ and the second row $(z_2)$ of $\mathbf{H}_1$. |
| − | * | + | *The second row is equal to $z_2 + z_3$ and the third row is $z_1 + z_3$. |
| − | * | + | *This is the identical code ⇒ rate $\underline{R = 4/7 = 0.571}$. |
| − | * | + | *Further, $w_{\rm Z} = 4$ and ${\rm E}[w_{\rm S}] = 1/7 \cdot [0 + 6 \cdot 2] = 12/7$. |
| − | + | '''(4)''' For this code with $n = 7$ (column count) and $m = 4$ (row count) holds: | |
| − | '''(4)''' | ||
:$$w_{\rm Z} = 4\hspace{0.05cm},\hspace{0.3cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n}w_{\rm S}(j) = 1/7 \cdot [3 + 1 + 2 +3+2 + 2+3] = 16/7\hspace{0.3cm} | :$$w_{\rm Z} = 4\hspace{0.05cm},\hspace{0.3cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n}w_{\rm S}(j) = 1/7 \cdot [3 + 1 + 2 +3+2 + 2+3] = 16/7\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} R \ge 1 - \frac{16/7}{4}= 3/7 \hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm} R \ge 1 - \frac{16/7}{4}= 3/7 \hspace{0.05cm}.$$ | ||
| − | + | The equal sign would only apply to linearly independent parity-check equations, which is not the case here: | |
| − | * | + | *The third row of $\mathbf{H}_3$ was taken from $\mathbf{H}_1$. |
| − | * | + | *If one deletes this row, $\mathbf{H}_3 = \mathbf{H}_2$ and therefore also holds: $\ \underline{R = 4/7 = 0.571}$. |
| − | '''(5)''' | + | '''(5)''' Here $n = 7$ and $m = 4$, as well as |
:$${\rm E}[w_{\rm S}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/8 \cdot [4 + 3 + 4 + 3 + 3+2 + 2+2] = 23/8\hspace{0.05cm},\hspace{0.8cm} | :$${\rm E}[w_{\rm S}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/8 \cdot [4 + 3 + 4 + 3 + 3+2 + 2+2] = 23/8\hspace{0.05cm},\hspace{0.8cm} | ||
{\rm E}[w_{\rm Z}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/4 \cdot [8 + 5 + 5+5] = 23/4$$ | {\rm E}[w_{\rm Z}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/4 \cdot [8 + 5 + 5+5] = 23/4$$ | ||
| Line 104: | Line 103: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Since all four equations are linearly independent, the code rate is equal to the lower bound: $\underline{R = 1/2}$. |
| − | <i> | + | <i>Hint:</i> This is the [[Aufgaben:Exercise_1.09:_Extended_Hamming_Code| "extended (8, 4, 4) Hamming code"]]. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:56, 10 December 2022
In this exercise, the code rates of the codes $\mathcal {C}_1, \, \mathcal {C}_2, \, \mathcal {C}_3$ and $\mathcal {C}_4$ are to be determined, where the codes are given by their test matrices alone. A lower bound on the code rate $R$ reads:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.05cm}.$$
If the $m$ parity-check equations of all matrix–rows are linearly independent, then the equal sign in the above inequality holds.
Used here is the following nomenclature:
- $w_{\rm Z}(j)$ with $1 ≤ j ≤ m$ being the "Hamming weight" of $j$th row of the parity-check matrix.
- By expectation value formation results:
- $${\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{m} w_{\rm Z}(j)\hspace{0.05cm}.$$
- Accordingly, $w_{\rm S}(i)$ with $1 ≤ i ≤ n$ gives the Hamming weight of $i$th column of $\mathbf{H}$ with expected value
- $${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n} w_{\rm S}(i)\hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Basics of Low–density Parity–check Code "s.
- Reference is made in particular to the page "Some characteristics of LDPC codes".
Questions
Solution
- This is the characteristic of a systematic code with $\underline{m = 3}$ parity-check equations.
- The code length is $\underline{n = 7}$.
- Thus, a codeword contains $\underline{k = 4}$ information bits.
Note: This is the "systematic (7, 4, 3)–Hamming code".
(2) The code rate of the (7, 4, 3)–Hamming–code is $\underline{R = 4/7 = 0.571}$.
- The Hamming weight for all $m = 3$ rows is $w_{\rm Z} = 4$ and for the mean Hamming–weight over all columns holds:
- $${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n} w_{\rm S}(j) = 1/7 \cdot [2 + 3 + 2+2 + 1+1 +1] = 12/7 \hspace{0.05cm}.$$
- This applies to the specified lower bound of the code rate:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{w_{\rm Z}} = 1 - \frac{12/7}{4}\hspace{0.15cm} \underline{= 4/7 \approx 0.571}\hspace{0.05cm}.$$
- This means: the actual code rate is equal to the lower bound ⇒ the $m = 3$ parity-check equations of $\mathbf{H}_1$ are linearly independent.
(3) The first row of $\mathbf{H}_2$ is the sum of the first row $(z_1)$ and the second row $(z_2)$ of $\mathbf{H}_1$.
- The second row is equal to $z_2 + z_3$ and the third row is $z_1 + z_3$.
- This is the identical code ⇒ rate $\underline{R = 4/7 = 0.571}$.
- Further, $w_{\rm Z} = 4$ and ${\rm E}[w_{\rm S}] = 1/7 \cdot [0 + 6 \cdot 2] = 12/7$.
(4) For this code with $n = 7$ (column count) and $m = 4$ (row count) holds:
- $$w_{\rm Z} = 4\hspace{0.05cm},\hspace{0.3cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n}w_{\rm S}(j) = 1/7 \cdot [3 + 1 + 2 +3+2 + 2+3] = 16/7\hspace{0.3cm} \Rightarrow \hspace{0.3cm} R \ge 1 - \frac{16/7}{4}= 3/7 \hspace{0.05cm}.$$
The equal sign would only apply to linearly independent parity-check equations, which is not the case here:
- The third row of $\mathbf{H}_3$ was taken from $\mathbf{H}_1$.
- If one deletes this row, $\mathbf{H}_3 = \mathbf{H}_2$ and therefore also holds: $\ \underline{R = 4/7 = 0.571}$.
(5) Here $n = 7$ and $m = 4$, as well as
- $${\rm E}[w_{\rm S}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/8 \cdot [4 + 3 + 4 + 3 + 3+2 + 2+2] = 23/8\hspace{0.05cm},\hspace{0.8cm} {\rm E}[w_{\rm Z}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/4 \cdot [8 + 5 + 5+5] = 23/4$$
- $$\Rightarrow \hspace{0.3cm}R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} = 1 - \frac{23/8}{23/4} = 1/2 \hspace{0.05cm}.$$
- Since all four equations are linearly independent, the code rate is equal to the lower bound: $\underline{R = 1/2}$.
Hint: This is the "extended (8, 4, 4) Hamming code".