Difference between revisions of "Aufgaben:Exercise 4.11Z: Error Probability with QAM"
m |
|||
| Line 4: | Line 4: | ||
[[File:P_ID1721__Mod_Z_4_10.png|right|frame|Tabelle zweier unterschiedlicher Gaußscher Fehlerfunktionen]] | [[File:P_ID1721__Mod_Z_4_10.png|right|frame|Tabelle zweier unterschiedlicher Gaußscher Fehlerfunktionen]] | ||
| − | + | We now make the following assumptions: | |
| − | * | + | * binary bipolar amplitude coefficients $a_ν ∈ \{±1\}$, |
| − | * | + | * rectangular fundamental transmission pulse with amplitude $s_0$ and bit time $T_{\rm B}$, |
| − | * | + | * AWGN noise with noise power density $N_0$, |
| − | * | + | * a receiver according to the matched-filter principle, |
| − | * | + | * the best possible demodulation and detection. |
| − | + | As has been shown several times, the bit error probability of binary phase modulation $\rm (BPSK)$ under these conditions can be calculated using the following equations: | |
:$$ p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ({s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$ | :$$ p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ({s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$ | ||
:$$\Rightarrow \hspace{0.3cm} p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$ | :$$\Rightarrow \hspace{0.3cm} p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$ | ||
| − | + | The corresponding equations of $\rm 4–QAM$ are: | |
:$$ p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/({2 \cdot T_{\rm B} }).$$ | :$$ p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/({2 \cdot T_{\rm B} }).$$ | ||
| − | + | Here it is taken into account that - in order to achieve the same transmission energy per bit as with BPSK - one must reduce the pulse amplitude $g_0$ of the square-wave impulses in the two sub-branches of 4-QAM by a factor of $\sqrt{2}$ . The envelope is then equal to $s_0$ for both systems. | |
| Line 28: | Line 28: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Quadrature_Amplitude_Modulation|Quadrature Amplitude Modulation]]. |
| − | * | + | *Reference is also made to the page [[Modulation_Methods/Lineare_digitale_Modulation#Fehlerwahrscheinlichkeiten_-_ein_kurzer_.C3.9Cberblick|Fehlerwahrscheinlichkeiten – ein kurzer Überblick]] in the previous chapter. |
| − | * | + | * Always assume the following numerical values: $s_0 = 2\,{\rm V}, \hspace{0.05cm} N_0 = 0.25 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}.$ |
| − | * | + | *The bit time is $T_{\rm B} = 1 \ \rm µ s$ (question 1) and $T_{\rm B} = 2 \ \rm µ s$ (from question 2 onwards). |
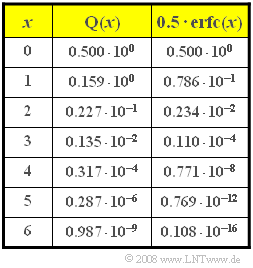
| − | *In | + | *In the table, the two common Gaussian error functions ${\rm Q}(x)$ and $1/2 \cdot {\rm erfc}(x)$ are given. |
| − | * | + | *Energies are to be given in $\rm V^2s$ ; thus, they refer to the reference resistance $R = 1 \ \rm \Omega$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| Line 60: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Mit den vorgegebenen Werten erhält man für ''Binary Phase Shift Keying'' (BPSK): | '''(1)''' Mit den vorgegebenen Werten erhält man für ''Binary Phase Shift Keying'' (BPSK): | ||
Revision as of 18:25, 19 March 2022
We now make the following assumptions:
- binary bipolar amplitude coefficients $a_ν ∈ \{±1\}$,
- rectangular fundamental transmission pulse with amplitude $s_0$ and bit time $T_{\rm B}$,
- AWGN noise with noise power density $N_0$,
- a receiver according to the matched-filter principle,
- the best possible demodulation and detection.
As has been shown several times, the bit error probability of binary phase modulation $\rm (BPSK)$ under these conditions can be calculated using the following equations:
- $$ p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ({s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$
- $$\Rightarrow \hspace{0.3cm} p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
The corresponding equations of $\rm 4–QAM$ are:
- $$ p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/({2 \cdot T_{\rm B} }).$$
Here it is taken into account that - in order to achieve the same transmission energy per bit as with BPSK - one must reduce the pulse amplitude $g_0$ of the square-wave impulses in the two sub-branches of 4-QAM by a factor of $\sqrt{2}$ . The envelope is then equal to $s_0$ for both systems.
Hints:
- This exercise belongs to the chapter Quadrature Amplitude Modulation.
- Reference is also made to the page Fehlerwahrscheinlichkeiten – ein kurzer Überblick in the previous chapter.
- Always assume the following numerical values: $s_0 = 2\,{\rm V}, \hspace{0.05cm} N_0 = 0.25 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}.$
- The bit time is $T_{\rm B} = 1 \ \rm µ s$ (question 1) and $T_{\rm B} = 2 \ \rm µ s$ (from question 2 onwards).
- In the table, the two common Gaussian error functions ${\rm Q}(x)$ and $1/2 \cdot {\rm erfc}(x)$ are given.
- Energies are to be given in $\rm V^2s$ ; thus, they refer to the reference resistance $R = 1 \ \rm \Omega$.
Questions
Solution
- $$E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} = \frac{1}{2}\cdot (2\,{\rm V})^2 \cdot 1\,{\rm µ s} = 2 \cdot 10^{-6}\,{\rm V^2s} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {E_{\rm B}}/{N_0} = \frac {2 \cdot 10^{-6}\,{\rm V^2s}}{0.25 \cdot 10^{-6}\,{\rm V^2/Hz}} = 8$$
- $$ \Rightarrow \hspace{0.3cm} p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{16} \right ) = {\rm Q}\left ( 4 \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{8}\right )\hspace{0.05cm}.$$
- Aufgrund der gegebenen $x$–Werte in der Tabelle ist bei dieser Teilaufgabe zweckmäßigerweise die erste Gleichung anzuwenden:
- $$p_\text{B, BPSK} = {\rm Q}\left ( 4 \right ) \hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4} }\hspace{0.05cm}.$$
(2) Bei doppelter Bitdauer ist auch die Energie doppelt so groß: $E_{\rm B} = 4 · 10^{–6} \ \rm V^2s$ ⇒ $E_{\rm B}/N_0 = 16$.
- Daraus folgt:
- $$p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{16}\right ) ={1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$
- Aus pragmatischen Gründen wurde hier die letzte Spalte der Tabelle benutzt.
(3) Setzt man die für die 4–QAM gegebenen Gleichungen ineinander ein, so kommt man zum gleichen Ergebnis wie bei der BPSK:
- $$p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \equiv p_\text{B, BPSK}.$$
- Da sich auch die Energie pro Bit gegenüber der Teilaufgabe (2) nicht geändert hat, wird sich auch die gleiche Fehlerwahrscheinlichkeit einstellen:
- $$p_{\rm B, \hspace{0.05cm}4-QAM}= {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$
(4) Richtig ist nur der erste Lösungsvorschlag:
- Die Fehlerwahrscheinlichkeit ist natürlich in den beiden Zweigen gleich groß. Warum auch nicht?
- Das würde allerdings bei einem Phasenversatz zwischen Sender und Empfänger nicht mehr gelten.
- Der Abstand der Nutzabtastwerte von der Schwelle ist hier allerdings $g_0$ und damit um den Faktor $\sqrt{2}$ kleiner als die Hüllkurve $s_0$ der gesamten 4–QAM.
- Betrachtet man den Inphase–Zweig (oder den Quadratur–Zweig) als eine eigenständige BPSK, so ist aber auch die Rauschleistung wegen der geringeren Symbolrate nur halb so groß wie bei der BPSK. Deshalb bleibt die Fehlerwahrscheinlichkeit gleich.