Aufgaben:Exercise 4.12: Calculations for the 16-QAM

• Return to book

Signalraumkonstellation der 16–QAM

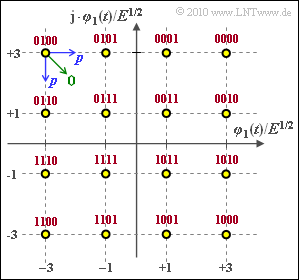
Beigefügte Grafik zeigt die Signalraumkonstellation der Quadraturamplitudenmodulation mit $M = 16$ Signalraumpunkten. Für dieses Modulationsverfahren sollen berechnet werden:

• die mittlere Energie pro Symbol bzw. pro Bit,
• die mittlere Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ sowie die Union Bound als obere Schranke,
• die mittlere Bitfehlerwahrscheinlichkeit $p_{\rm B}$ bei Graycodierung. Die Gray–Zuordnung ist in der Grafik angegeben (rote Beschriftung).

Hinweise:

• Die Aufgabe behandelt einen Teilaspekt des Kapitels Trägerfrequenzsysteme mit kohärenter Demodulation.
• Die Wahrscheinlichkeit, dass das linke obere Symbol in eines der benachbarten Symbole verfälscht wird, wird mit $p$ abgekürzt (blaue Pfeile in der Grafik).
• Eine diagonale Verfälschung  ⇒  zwei Bit verfälscht (grüner Pfeil) wird ausgeschlossen.
• Für den AWGN–Kanal gilt mit dem komplementären Gaußschen Fehlerintegrale für diese Hilfsgröße:

$$p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right ) \hspace{0.05cm}.$$

• Verwenden Sie für numerische Berechnungen $E = 1 \ \rm mWs$ und $p = 0.004$. Aus diesen Werten kann die AWGN–Rauschleistungsdichte $N_0$ näherungsweise berechnet werden:

$$p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right ) = 0.004 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} \frac{ 2E}{ N_0} \approx 2.65^2 \approx 7 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_0 = \frac{ E}{ 3.5}\approx 1.4 \cdot 10^{-4}\,{\rm W/Hz} \hspace{0.05cm}.$$

Fragebogen

1

Es sei $E = 0.001 \ \rm Ws$. Wie groß ist die mittlere Energie pro Symbol?

$E_{\rm S}$ = $\ \cdot 10^{\rm –2} \ \rm Ws$

2

Wie groß ist die mittlere Energie pro Bit?

$E_{\rm B}$ = $\ \cdot 10^{\rm –2} \ \rm mW$

3

Geben Sie die (verbesserte) „Union Bound” ($p_{\rm UB}$) mit $p = 0.4\%$ an.

$p_{\rm UB}$ =

4

Berechnen Sie die tatsächliche Symbolfehlerwahrscheinlichkeit $p_{\rm S} < p_{\rm UB}$.

$p_{\rm S}$ =

5

Berechnen Sie die tatsächliche Bitfehlerwahrscheinlichkeit bei Graycodierung.

$p_{\rm B}$ =

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)