Difference between revisions of "Aufgaben:Exercise 4.12: Regular and Irregular Tanner Graph"
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes}} | {{quiz-Header|Buchseite=Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes}} | ||
| − | [[File:P_ID3072__KC_A_4_12_v1.png|right|frame| | + | [[File:P_ID3072__KC_A_4_12_v1.png|right|frame|Tanner graph for code $\rm A$]] |
| − | + | Shown is a Tanner graph of a code $\rm A$ with | |
| − | * the | + | * the variable nodes $V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_6$, . where $V_i$ denotes the $i$<sup>th</sup> code word bit $($whether information bit or parity bit$)$ and corresponds to the $i$<sup>th</sup> column of the parity-check matrix; |
| − | |||
| + | * the check nodes</i> $C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_3$, which represent the rows of the $\mathbf{H}_{\rm A}$ matrix and hence the parity-check equations. | ||
| − | |||
| + | An edge between $V_i$ and $C_j$ indicates that the $i$<sup>th</sup> code word symbol is involved in the $j$<sup>th</sup> parity-check equation. In this case, the element $h_{j,\hspace{0.05cm}i}$ of the parity-check matrix is equal $1$. | ||
| − | In | + | In this exercise, the relation between the above Tanner graph $($valid for the code $\rm A)$ and the matrix $\mathbf{H}_{\rm A}$ shall be given. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In addition, the Tanner graph to a parity-check matrix $\mathbf{H}_{\rm B}$ shall be set up, resulting from $\mathbf{H}_{\rm A}$ adding another row. This is to be determined so that the associated code $\rm B$ is regular. This means: | ||
| + | * From all variable nodes $V_i$ $($with $1 ≤ i ≤ n)$ go off an equal number of edges, <br>likewise from all check nodes $C_j$ $($with $1 ≤ j ≤ m)$. | ||
| + | * The Hamming weights of all rows of $\mathbf{H}_{\rm B}$ are each said to be equal $(w_{\rm R})$, as are the Hamming weights of all columns $(w_{\rm C})$. | ||
| + | * For the rate of the regular code $\rm B$ to be constructed, the following lower bound then applies: | ||
| + | :$$R \ge 1 - \frac{w_{\rm C}}{w_{\rm R}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | <u>Hints:</u> | ||
| + | *This exercise belongs to the chapter [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes|"Basics of Low–density Parity–check Codes"]]. | ||
| − | + | *Reference is made in particular to the section [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Two-part_LDPC_graph_representation_-_Tanner_graph|"Two-part LDPC graph representation – Tanner graph"]]. | |
| − | |||
| − | *Reference is made in particular to the | ||
| Line 41: | Line 42: | ||
{Which statements are true based on the Tanner graph? | {Which statements are true based on the Tanner graph? | ||
|type="[]"} | |type="[]"} | ||
| − | + The row 1 of $\mathbf{H}_{\rm A}$& | + | + The row 1 of the $\mathbf{H}_{\rm A}$ matrix is "$1 \ 1 \ 0 \ 1 \ 0 \ 0$". |
| − | - The row 2 of $\mathbf{H}_{\rm A}$& | + | - The row 2 of the $\mathbf{H}_{\rm A}$ matrix is "$1 \ 0 \ 1 \ 0 \ 0 \ 1$". |
| − | + The row 3 of $\mathbf{H}_{\rm A}$& | + | + The row 3 of the $\mathbf{H}_{\rm A}$ matrix is "$0 \ 1 \ 1 \ 0 \ 0 \ 1$". |
| − | {What are the properties of | + | {What are the properties of code $\rm A$ ? |
|type="[]"} | |type="[]"} | ||
+ The code is systematic. | + The code is systematic. | ||
| Line 52: | Line 53: | ||
- The code rate is $R = 1/3$. | - The code rate is $R = 1/3$. | ||
| − | {The matrix $\mathbf{H}_{\rm B}$ is obtained from $\mathbf{H}_{\rm A}$ by adding one more row. By which fourth row does a regular code $\rm B$ result? | + | {The matrix $\mathbf{H}_{\rm B}$ is obtained from $\mathbf{H}_{\rm A}$ by adding one more row. By which fourth row does a regular code $\rm B$ result? |
|type="[]"} | |type="[]"} | ||
+By adding "$0 \ 0 \ 0 \ 1 \ 1 \ 1$". | +By adding "$0 \ 0 \ 0 \ 1 \ 1 \ 1$". | ||
| Line 58: | Line 59: | ||
- By adding any other row. | - By adding any other row. | ||
| − | {What are the properties of | + | {What are the properties of code $\rm B$? |
|type="[]"} | |type="[]"} | ||
- The code is systematic. | - The code is systematic. | ||
| Line 68: | Line 69: | ||
===Solutiojn=== | ===Solutiojn=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The number of $\mathbf{H}_{\rm A}$& | + | '''(1)''' The number of $\mathbf{H}_{\rm A}$ rows is equal to the number of check nodes $C_j$ in the Tanner graph ⇒ $\underline{m = 3}$, <br>and the number $\underline{n = 6}$ of variable nodes $V_i$ is equal to the column number. |
| + | [[File:P_ID3073__KC_A_4_12c_v1.png|right|frame|Underlying parity-check equations]] | ||
| − | '''(2)''' Correct are <u>answers 1 and 3</u> in contrast to statement 2: | + | '''(2)''' Correct are the <u>answers 1 and 3</u> in contrast to statement 2: |
| − | *The second $\mathbf{H}_{\rm A}$& | + | *The second $\mathbf{H}_{\rm A}$ row is rather "$1 \ 0 \ 1 \ 0 \ 1 \ 0$". |
| − | |||
| − | |||
| + | *Thus, this exercise is based on the following parity-check equation: | ||
:$${ \boldsymbol{\rm H}}_{\rm A} = | :$${ \boldsymbol{\rm H}}_{\rm A} = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 84: | Line 85: | ||
\end{pmatrix}\hspace{0.05cm}.$$ | \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | *In the diagram, the parity-check equations are illustrated as red (row 1), green (row 2) | + | *In the diagram, the parity-check equations are illustrated as red (row 1), green (row 2) resp. blue (row 3) groupings. |
| − | '''(3)''' Correct are <u>solutions 1 and 3</u>: | + | '''(3)''' Correct are the <u>solutions 1 and 3</u>: |
| − | * The $\mathbf{H}$ matrix ends with a $3 × 3$ diagonal matrix ⇒ systematic code | + | * The $\mathbf{H}$ matrix ends with a $3 × 3$ diagonal matrix ⇒ systematic code. |
| − | |||
| − | |||
| − | |||
| + | * Thus, the Hamming weights of the last three columns are $w_{\rm C}(4) = w_{\rm C}(5) = w_{\rm C}(6) = 1$. | ||
| + | |||
| + | * For the first three columns, $w_{\rm C}(1) = w_{\rm C}(2) = w_{\rm C}(3) = 2$ ⇒ irregular code. | ||
| + | * The three matrix rows are linearly independent. | ||
| − | [[File: P_ID3074__KC_A_4_12d_v1.png|right|frame|Modified Tanner graph for code $\rm B$]] | + | *Thus $k = n - m = 6 - 3 = 3$ and $R = k/n = 1/2$ holds. |
| − | '''(4)''' Correct is the <u>proposed solution 1</u>: | + | |
| − | *Looking at the previous Tanner& | + | |
| − | *By adding the row "$0 \ 0 \ 0 \ 1 \ 1 \ 1$" to the $\mathbf{H}_{\rm A}$ matrix, one obtains: | + | |
| + | [[File: P_ID3074__KC_A_4_12d_v1.png|right|frame|Modified Tanner graph for code $\rm B$]] | ||
| + | '''(4)''' Correct is the <u>proposed solution 1</u>: | ||
| + | *Looking at the previous Tanner graph, one can see the correctness of the proposed solution 1. | ||
| + | |||
| + | *By adding the row "$0 \ 0 \ 0 \ 1 \ 1 \ 1$" to the $\mathbf{H}_{\rm A}$ matrix, one obtains: | ||
:$${ \boldsymbol{\rm H}}_{\rm B} = | :$${ \boldsymbol{\rm H}}_{\rm B} = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 108: | Line 115: | ||
\end{pmatrix}\hspace{0.05cm}.$$ | \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | The modifications are marked in red in the adjacent graphic. | + | :The modifications are marked in red in the adjacent graphic. |
| − | Due to the newly added check node $C_4$ and the connections with $V_4, \ V_5$ and $V_6$, there are now | + | *Due to the newly added check node $C_4$ and the connections with $V_4, \ V_5$ and $V_6$, there are now |
| − | * from all variable nodes $V_i$ two lines, and | + | :* from all variable nodes $V_i$ two lines, and |
| − | |||
| + | :* from all check nodes $C_j$ uniformly four. | ||
| + | *This is the condition for the code $\rm B$ to be regular. | ||
| − | |||
| − | + | '''(5)''' Correct are the <u>solutions 2 and 3</u>: | |
| − | '''(5)''' Correct are the <u>solutions 2 and 3</u>: | + | *The construction in subtask '''(4)''' yields a regular code. |
| − | *The construction in subtask (4) yields a regular code. | + | |
| − | *The Hamming weights of the rows and columns, respectively, are $w_{\rm | + | *The Hamming weights of the rows and columns, respectively, are $w_{\rm R} = 3$ and $w_{\rm C} = 2$. |
*This gives as lower bound for the code rate: | *This gives as lower bound for the code rate: | ||
| − | :$$R \ge 1 - \frac{w_{\rm | + | :$$R \ge 1 - \frac{w_{\rm C}}{w_{\rm R}} |
= 1 - {2}/{3} = 1/3 | = 1 - {2}/{3} = 1/3 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The $\mathbf{H}$ manipulation does not change the generator matrix $\mathbf{G}$. | + | *The $\mathbf{H}$ manipulation does not change the generator matrix $\mathbf{G}$. |
| − | *The same code is still sent with code rate $R = 1/2$. | + | |
| + | *The same code is still sent with code rate $R = 1/2$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 17:39, 17 December 2022
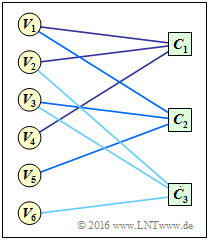
Shown is a Tanner graph of a code $\rm A$ with
- the variable nodes $V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_6$, . where $V_i$ denotes the $i$th code word bit $($whether information bit or parity bit$)$ and corresponds to the $i$th column of the parity-check matrix;
- the check nodes $C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_3$, which represent the rows of the $\mathbf{H}_{\rm A}$ matrix and hence the parity-check equations.
An edge between $V_i$ and $C_j$ indicates that the $i$th code word symbol is involved in the $j$th parity-check equation. In this case, the element $h_{j,\hspace{0.05cm}i}$ of the parity-check matrix is equal $1$.
In this exercise, the relation between the above Tanner graph $($valid for the code $\rm A)$ and the matrix $\mathbf{H}_{\rm A}$ shall be given.
In addition, the Tanner graph to a parity-check matrix $\mathbf{H}_{\rm B}$ shall be set up, resulting from $\mathbf{H}_{\rm A}$ adding another row. This is to be determined so that the associated code $\rm B$ is regular. This means:
- From all variable nodes $V_i$ $($with $1 ≤ i ≤ n)$ go off an equal number of edges,
likewise from all check nodes $C_j$ $($with $1 ≤ j ≤ m)$.
- The Hamming weights of all rows of $\mathbf{H}_{\rm B}$ are each said to be equal $(w_{\rm R})$, as are the Hamming weights of all columns $(w_{\rm C})$.
- For the rate of the regular code $\rm B$ to be constructed, the following lower bound then applies:
- $$R \ge 1 - \frac{w_{\rm C}}{w_{\rm R}} \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Basics of Low–density Parity–check Codes".
- Reference is made in particular to the section "Two-part LDPC graph representation – Tanner graph".
Questions
Solutiojn
and the number $\underline{n = 6}$ of variable nodes $V_i$ is equal to the column number.
(2) Correct are the answers 1 and 3 in contrast to statement 2:
- The second $\mathbf{H}_{\rm A}$ row is rather "$1 \ 0 \ 1 \ 0 \ 1 \ 0$".
- Thus, this exercise is based on the following parity-check equation:
- $${ \boldsymbol{\rm H}}_{\rm A} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$
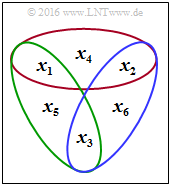
- In the diagram, the parity-check equations are illustrated as red (row 1), green (row 2) resp. blue (row 3) groupings.
(3) Correct are the solutions 1 and 3:
- The $\mathbf{H}$ matrix ends with a $3 × 3$ diagonal matrix ⇒ systematic code.
- Thus, the Hamming weights of the last three columns are $w_{\rm C}(4) = w_{\rm C}(5) = w_{\rm C}(6) = 1$.
- For the first three columns, $w_{\rm C}(1) = w_{\rm C}(2) = w_{\rm C}(3) = 2$ ⇒ irregular code.
- The three matrix rows are linearly independent.
- Thus $k = n - m = 6 - 3 = 3$ and $R = k/n = 1/2$ holds.
(4) Correct is the proposed solution 1:
- Looking at the previous Tanner graph, one can see the correctness of the proposed solution 1.
- By adding the row "$0 \ 0 \ 0 \ 1 \ 1 \ 1$" to the $\mathbf{H}_{\rm A}$ matrix, one obtains:
- $${ \boldsymbol{\rm H}}_{\rm B} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1\\ 0 &0 &0 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$
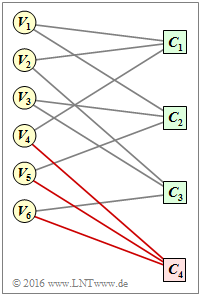
- The modifications are marked in red in the adjacent graphic.
- Due to the newly added check node $C_4$ and the connections with $V_4, \ V_5$ and $V_6$, there are now
- from all variable nodes $V_i$ two lines, and
- from all check nodes $C_j$ uniformly four.
- This is the condition for the code $\rm B$ to be regular.
(5) Correct are the solutions 2 and 3:
- The construction in subtask (4) yields a regular code.
- The Hamming weights of the rows and columns, respectively, are $w_{\rm R} = 3$ and $w_{\rm C} = 2$.
- This gives as lower bound for the code rate:
- $$R \ge 1 - \frac{w_{\rm C}}{w_{\rm R}} = 1 - {2}/{3} = 1/3 \hspace{0.05cm}.$$
- The $\mathbf{H}$ manipulation does not change the generator matrix $\mathbf{G}$.
- The same code is still sent with code rate $R = 1/2$.