Difference between revisions of "Aufgaben:Exercise 4.13Z: AMI Code"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Power-Spectral_Density |
}} | }} | ||
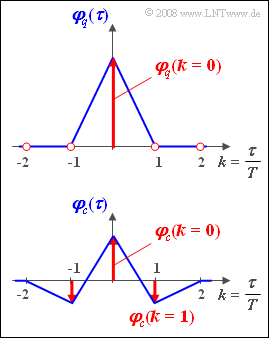
| − | [[File:P_ID427__Sto_Z_4_13.png|right|frame| | + | [[File:P_ID427__Sto_Z_4_13.png|right|frame|ACF at AMI coding]] |
| − | + | For spectral adaptation (shaping) of a digital signal to the characteristics of the channel, one uses so-called <i>pseudo-ternary codes</i>. In these codes, the binary source symbol sequence $\langle q_\nu \rangle$ is converted to a sequence $\langle c_\nu \rangle$ of ternary symbols according to a fixed rule: | |
:$$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$ | :$$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$ | ||
| − | + | The best known representative of this code class is the AMI code (from <i>Alternate Mark Inversion</i>). Here. | |
| − | * | + | *the binary value $q_\nu = -1$ is always mapped to $c_\nu = 0$ , |
| − | * | + | *while $q_\nu = +1$ is alternately represented by the ternary values $c_\nu = +1$ and $c_\nu = -1$ . |
| − | + | By convention, the ternary symbol $c_\nu = +1$ shall be selected at the first occurrence of $q_\nu = +1$ . | |
| − | + | It is further assumed that | |
| − | * | + | *the two possible source symbols are each equally probable and |
| − | * | + | *the source symbol sequence $\langle q_\nu \rangle $ has no internal statistical bindings. |
| − | + | Thus, all discrete ACF values are zero except $\varphi_q(k=0)$: | |
:$$\varphi_q ( k \cdot T) = 0 \hspace{0.5cm} {\rm f alls} \hspace{0.5cm} k \not= 0.$$ | :$$\varphi_q ( k \cdot T) = 0 \hspace{0.5cm} {\rm f alls} \hspace{0.5cm} k \not= 0.$$ | ||
| − | + | Here $T$ denotes the distance between sources– or code symbols. Use the value $T = 1 \hspace{0.05cm} \rm µ s$. | |
| − | + | The figure shows the given auto-correlation functions. Please note: | |
| − | * | + | * In red are respectively the discrete-time representations ${\rm A} \{ \varphi_q(\tau) \}$ and ${\rm A} \{ \varphi_c(\tau) \}$ of the auto-correlation functions, each with the reference value $T$. |
| − | * | + | * The functions shown in blue indicate the continuous-time progressions $\varphi_q(\tau)$ and $\varphi_c(\tau)$ of the ACF, assuming square-wave pulses. |
| Line 35: | Line 35: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Power-Spectral_Density|Power-Spectral Density]]. |
| − | * | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-Correlation Function]] as well as to the page [[Theory_of_Stochastic_Signals/Power-Spectral_Density#Numerical_PSD_determination|Numerical PSD determination]]. |
*Benutzen Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t = 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet: | *Benutzen Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t = 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet: | ||
| Line 44: | Line 44: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the discrete ACF–value of the source symbols for $k = 0$? |
|type="{}"} | |type="{}"} | ||
$\varphi_q(k=0) \ = \ $ { 1 3% } | $\varphi_q(k=0) \ = \ $ { 1 3% } | ||
| − | { | + | {Which statements are valid for the PSD–functions ${\it \Phi}_q(f)$ and ${\rm P} \{ {\it \Phi}_q(f) \}$? |
|type="[]"} | |type="[]"} | ||
| − | + ${\rm P} \{ {\it \Phi}_q(f) \}$ | + | + ${\rm P} \{ {\it \Phi}_q(f) \}$ is a constant for all frequencies. |
| − | - ${\it \Phi}_q(f)$ | + | - ${\it \Phi}_q(f)$ is constant for $|f \cdot T| < 0.5$ and outside zero. |
| − | + ${\it \Phi}_q(f)$ | + | + ${\it \Phi}_q(f)$ proceeds $\rm si^2$-shaped. |
| − | { | + | {The source symbol sequence is $\langle q_\nu \rangle = \langle +1, -1, +1, +1, -1, +1, +1, -1, -1, -1 \rangle$. |
| − | <br> | + | <br>What are the code symbols $c_\nu$ ? Enter the code symbol $c_6$ . |
|type="{}"} | |type="{}"} | ||
| − | $c_6 \ = \ $ { -1.01--0.99 | + | $c_6 \ = \ $ { -1.01--0.99 } |
| − | { | + | {What is the discrete ACF–value of the code symbols for $k = 0$. |
|type="{}"} | |type="{}"} | ||
$\varphi_c(k=0) \ = \ $ { 0.5 3% } | $\varphi_c(k=0) \ = \ $ { 0.5 3% } | ||
| − | { | + | {Calculate the ACF values $\varphi_c(k=+1)$ and $\varphi_c(k=-1)$. |
|type="{}"} | |type="{}"} | ||
$\varphi_c(k=+1) \ = \ $ { -0.26--0.24 } | $\varphi_c(k=+1) \ = \ $ { -0.26--0.24 } | ||
| Line 77: | Line 77: | ||
| − | { | + | {What power spectral density ${\it \Phi}_c(f)$ results for frequency $f=0$ or for $f = 500 \hspace{0.08cm} \rm kHz$. <i>Note:</i> For $|k| \ge 2$ all ACF–values $\varphi_c(k) are \equiv 0$. |
|type="{}"} | |type="{}"} | ||
${\it \Phi}_c(f = 0) \ = \ $ { 0. } $\ \cdot 10^{-6} \ \rm 1/Hz$ | ${\it \Phi}_c(f = 0) \ = \ $ { 0. } $\ \cdot 10^{-6} \ \rm 1/Hz$ | ||
| − | ${\it \Phi}_c(f = 500 | + | ${\it \Phi}_c(f = 500 \hspace{0.08cm} \rm kHz)\ = \ $ { 0.405 3% } $\ \cdot 10^{-6} \ \rm 1/Hz$ |
| + | $c_6 \ = \ $ { -1.01--0.99 } | ||
| Line 86: | Line 87: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Der diskrete AKF-Wert für $k = 0$ gibt den quadratischen Mittelwert (hier gleich der Varianz) der Quellensymbole an. | '''(1)''' Der diskrete AKF-Wert für $k = 0$ gibt den quadratischen Mittelwert (hier gleich der Varianz) der Quellensymbole an. | ||
Revision as of 21:49, 7 March 2022
For spectral adaptation (shaping) of a digital signal to the characteristics of the channel, one uses so-called pseudo-ternary codes. In these codes, the binary source symbol sequence $\langle q_\nu \rangle$ is converted to a sequence $\langle c_\nu \rangle$ of ternary symbols according to a fixed rule:
- $$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$
The best known representative of this code class is the AMI code (from Alternate Mark Inversion). Here.
- the binary value $q_\nu = -1$ is always mapped to $c_\nu = 0$ ,
- while $q_\nu = +1$ is alternately represented by the ternary values $c_\nu = +1$ and $c_\nu = -1$ .
By convention, the ternary symbol $c_\nu = +1$ shall be selected at the first occurrence of $q_\nu = +1$ .
It is further assumed that
- the two possible source symbols are each equally probable and
- the source symbol sequence $\langle q_\nu \rangle $ has no internal statistical bindings.
Thus, all discrete ACF values are zero except $\varphi_q(k=0)$:
- $$\varphi_q ( k \cdot T) = 0 \hspace{0.5cm} {\rm f alls} \hspace{0.5cm} k \not= 0.$$
Here $T$ denotes the distance between sources– or code symbols. Use the value $T = 1 \hspace{0.05cm} \rm µ s$.
The figure shows the given auto-correlation functions. Please note:
- In red are respectively the discrete-time representations ${\rm A} \{ \varphi_q(\tau) \}$ and ${\rm A} \{ \varphi_c(\tau) \}$ of the auto-correlation functions, each with the reference value $T$.
- The functions shown in blue indicate the continuous-time progressions $\varphi_q(\tau)$ and $\varphi_c(\tau)$ of the ACF, assuming square-wave pulses.
Hints:
- This exercise belongs to the chapter Power-Spectral Density.
- Reference is also made to the chapter Auto-Correlation Function as well as to the page Numerical PSD determination.
- Benutzen Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t = 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet:
- $${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$
Questions
Solution
- Da $q_\nu$ nur die Werte $-1$ und $+1$ annehmen kann, ist $\varphi_q(k=0)\hspace{0.15cm}\underline{= 1}$.
(2) Richtig sind die Lösungsvorschläge 1 und 3:
- Die zeitdiskrete AKF und deren Fouriertransformierte lauten:
- $${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$
- Es ist berücksichtigt, dass $\varphi_q(k=0)= \sigma_q^2= 1$ ist. Das bedeutet:
- Die periodische Fortsetzung von ${\rm P} \{ {\it \Phi}_q(f) \}$ ergibt somit für alle Frequenzen den gleichen Wert.
- Dagegen kann die zeitkontinuierliche AKF wie folgt dargestellt werden:
- $$ \varphi_q ( \tau ) = {\rm A} \{ \varphi_q ( \tau ) \} \star ( {\rm \Delta} ( \tau) / T ).$$
- Das dazugehörige Leistungsdichtespektrum (Fouriertransformierte der AKF) ist dann das Produkt der Fouriertransformierten der beiden Faltungsterme:
- $$ {\it \Phi_q} ( f) = {\rm P} \{ {\it \Phi_q}( f) \} \cdot {\rm si}^2 (\pi f T ) = T \cdot {\rm si}^2 (\pi f T ) .$$
- Aufgrund der gewählten AKF-Interpolation (mit Geradenabschnitten) aus ihren Abtastwerten ergibt sich ein $\rm si^2$-förmiges LDS.
- Ein rechteckförmiges Spektrum gemäß Lösungsvorschlag (2) würde sich nur bei $\rm si$-förmiger Interpolation einstellen.
(3) Die codierte Folge lautet: $\langle +1, \ 0, -1, +1, \ 0, -1, +1, \ 0, \ 0, \ 0 \rangle$. Das 6. Symbol ist somit $c_6\hspace{0.15cm}\underline{= -1}$.
(4) Die Auftrittswahrscheinlichkeiten der Werte $-1$ , $\ 0$ und $+1$ sind $0.25, 0.5, 0.25$. Daraus folgt:
- $$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}. $$
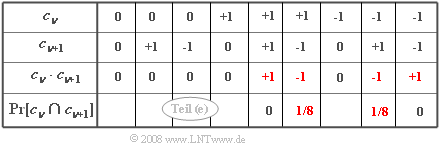
(5) Für den AKF-Wert bei $k = 1$ betrachtet man das Produkt $c_{\nu} \cdot c_{\nu+1}$. Es ergeben sich die rechts gezeigten Kombinationen.
- Einen Beitrag liefern nur Produkte $c_{\nu} \cdot c_{\nu+1} \ne 0$ mit ${\rm Pr}\big[c_{\nu} \cdot c_{\nu+1}\big] \ne 0$:
- $$\varphi_c ( k = 1) = {\rm Pr} \big [( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] \cdot (+1) \cdot (-1) + {\rm Pr} \big [ ( c_{\nu} = -1) \cap ( c_{\nu + 1} = +1) \big ] \cdot (-1) \cdot (+1).$$
- In der Tabelle sind diese Terme rot gekennzeichnet. Weiter gilt:
- $$ {\rm Pr} \big [ ( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] = $$
- $$ = {\rm Pr} ( c_{\nu} = +1) \cdot {\rm Pr} \left ( c_{\nu + 1} = -1 | c_{\nu } = +1) \right ) = \frac{1}{4} \cdot \frac{1}{2}= \frac{1}{8} . $$
- Hierbei ist vorausgesetzt, dass $+1$ mit der Wahrscheinlichkeit $0.25$ auftritt und danach $-1$ nur in der Hälfte der Fälle folgt.
- Das gleiche Ergebnis erhält man für den zweiten Beitrag. Damit gilt:
- $$\varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$
- $$\varphi_c ( k = -1) = \varphi_c ( k = 1) \hspace{0.15cm}\underline{= -0.25}.$$
- Zur Berechnung von $\varphi_c ( k = 2)$ muss über $3^3 = 27$ Kombinationen gemittelt werden. Das Ergebnis ist Null.
(6) Die Fouriertransformierte der zeitdiskreten AKF ${\rm A} \{ \varphi_c(\tau) \}$ lautet:
- $$P \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$
- Mit dem Ergebnis der letzten Teilaufgabe folgt daraus:
- $$P \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$
- Wie unter Punkt (2) gezeigt, gilt dann für das LDS – also die Fouriertransformierte von $\varphi_c(\tau)$:
- $${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm si}^2 ( \pi f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$
- $$\Rightarrow \hspace{0.3cm} {\it \Phi_c}( f = 0) \hspace{0.15cm}\underline{= 0}, \hspace{0.8cm} {\it \Phi_c}( f = {\rm500 \hspace{0.1cm}kHz}) = T \cdot \frac {{\rm sin}^4 ( \pi /2 )}{( \pi /2 )^2 } = \frac {4 T}{\pi^2} \rm \hspace{0.15cm}\underline{= 0.405 \cdot 10^{-6} \ {1}/{Hz}}.$$