Difference between revisions of "Aufgaben:Exercise 4.15: MSK Compared with BPSK and QPSK"
m (→Questions) |
m (→Solution) |
||
| Line 77: | Line 77: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' From the equation and graph it can be seen that in the case of ''Binary Phase Shift Keying'' $\rm (BPSK)$ , the first zero of the power-spectral densityis at $f_1\hspace{0.15cm}\underline{ =1} \cdot 1/T_{\rm B}$ . |
| − | '''(2)''' | + | '''(2)''' Due to the lower symbol rate $1/T$,i ''Quaternary Phase Shift Keying'' $\rm (QPSK)$ – as well as all related quarternary modulation methods – has a spectrum half as wide as in BPSK ⇒ $f_1\hspace{0.15cm}\underline{ =0.5} \cdot 1/T_{\rm B}$. |
| − | '''(3)''' | + | '''(3)''' The power-spectral density $\rm (PSD)$ of the total signal in the equivalent low-pass range is given by: |
:$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) + {\it \Phi}_{s,\hspace{0.05cm} {\rm Q},\hspace{0.05cm} {\rm TP}}(f)= 2 \cdot {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = {1}/{ T} \cdot |G(f)|^2\hspace{0.05cm}.$$ | :$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) + {\it \Phi}_{s,\hspace{0.05cm} {\rm Q},\hspace{0.05cm} {\rm TP}}(f)= 2 \cdot {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = {1}/{ T} \cdot |G(f)|^2\hspace{0.05cm}.$$ | ||
| − | + | This takes into account, that | |
| − | * | + | * the signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ are uncorrelated sind, such that one can add the PSD components, |
| − | * | + | * and that the expected value is $E[a_ν^2] = 1$ , due to the binary bipolar amplitude coefficients. |
| − | + | This gives: | |
:$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{1}{ T} \cdot \left ( \frac {4}{\pi} \right ) ^2 \cdot g_0^2 \cdot T^2 \cdot \frac{ {\rm cos}^2 ( 2 \pi f T )}{ \big [1 - (4 f T)^2 \big ] ^2} \hspace{0.05cm}.$$ | :$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{1}{ T} \cdot \left ( \frac {4}{\pi} \right ) ^2 \cdot g_0^2 \cdot T^2 \cdot \frac{ {\rm cos}^2 ( 2 \pi f T )}{ \big [1 - (4 f T)^2 \big ] ^2} \hspace{0.05cm}.$$ | ||
| − | + | With $s_0 = g_0$, $T = T_{\rm B}$ and $E_{\rm B} = s_0^2 · T_{\rm B}/2$ , it further holds that: | |
:$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{32}{ \pi^2} \cdot E_{\rm B} \cdot \frac{ {\rm cos}^2 ( 2 \pi \cdot f \cdot T_{\rm B} )}{ \big [1 - (4 \cdot f \cdot T_{\rm B})^2 \big ] ^2}\hspace{0.3cm} | :$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{32}{ \pi^2} \cdot E_{\rm B} \cdot \frac{ {\rm cos}^2 ( 2 \pi \cdot f \cdot T_{\rm B} )}{ \big [1 - (4 \cdot f \cdot T_{\rm B})^2 \big ] ^2}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f = 0 )= \frac{32}{ \pi^2} \cdot E_{\rm B} \hspace{0.15cm}\underline {\approx 3.243 \cdot E_{\rm B}} \hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm} {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f = 0 )= \frac{32}{ \pi^2} \cdot E_{\rm B} \hspace{0.15cm}\underline {\approx 3.243 \cdot E_{\rm B}} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Only <u>Answer 2</u> is correct: |
| − | * | + | *It can already be seen from the graph that the first statement is false and the second is correct. |
| − | * | + | (𝐸B/𝑇B). |
| − | * | + | *Answer 3 is also incorrect. The integral over the power-spectral densities yields the power $(E_{\rm B}/T_{\rm B})$. |
| + | *The signal waveforms of BPSK, QPSK and MSK make it clear that the power with a constant envelope $(s_0)$ is the same for these three modulation methods. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 18:22, 21 March 2022
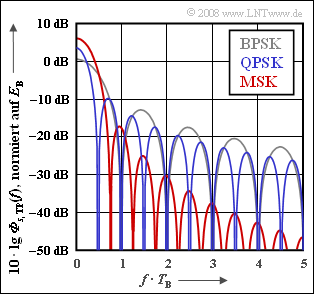
Compare the power-spectral densities (in the equivalent low-pass range) of
- Binary Phase Shift Keying $\rm (BPSK)$,
- Quaternary Phase Shift Keying $\rm (QPSK)$,
- Minimum Shift Keying $\rm (MSK)$.
These are shown logarithmically in the graph, with frequency normalized to the reciprocal of the bit duration $T_{\rm B}$ .
For both BPSK and QPSK, a rectangular fundamental pulse of height $s_0$ and symbol duration $T$ is assumed. Thus, for BPSK and QPSK (as well as 4-QAM and offset QPSK), the same applies:
- $${\it \Phi}_{s}(f) = \frac{s_0^2 \cdot T}{4} \cdot \big [ {\rm si}^2 ( \pi T \cdot (f- f_{\rm T}) ) + {\rm si}^2 ( \pi T \cdot (f+ f_{\rm T}) ) \big ]\hspace{0.05cm},$$
and transformed into the equivalent low-pass range:
- $$ {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 ( \pi f T ) \hspace{0.05cm}.$$
Despite having the same formula, BPSK and QPSK have different power-spectral densities:
- In BPSK (grey curve) the symbol duration $T$ is equal to the bit duration $T_{\rm B}$ with an energy per bit of $(E_{\rm B} = s_0^2 · T_{\rm B}/2)$ , it holds that:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = E_{\rm B} \cdot {\rm si}^2 ( \pi f T_{\rm B} ) \hspace{0.05cm}.$$
- In contrast, in QPSK (blue curve) for the same $E_{\rm B}$ , the symbol duration $T$ is doubled:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = 2 \cdot E_{\rm B} \cdot {\rm si}^2 ( 2\pi f T_{\rm B} ) \hspace{0.05cm}.$$
When calculating the MSK spectrum (red curve), one can take into account that MSK can be realized as an offset QPSK as in the block diagram in the theory section if the following fundamental pulse is used:
- $$g(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{otherwise}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm }\hspace{0.05cm}. \\ \end{array}$$
The corresponding spectral function is calculated in Exercise 4.15Z :
- $$G(f) = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$
Additionally, consider:
- The two signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ are uncorrelated despite prior encoding.
- For MSK, contrary to QPSK, one should set $T = T_{\rm B}$ as in BPSK.
- Also, the energy per bit in MSK is given as: $E_{\rm B} = s_0^2 · T/2$.
- The magnitude of the low-pass signal $|s_{\rm TP}(t)| = s_0$ is equal to the maximum value $g_0$ of the fundamental pulse $g(t)$.
Hints:
- This exercise belongs to the chapter Nonlinear Digital Modulation.
- Particular reference is made to the section Realizing MSK as Offset–QPSK.
- The power-spectral density in the equivalent low-pass range of one branch – for example: the in-phase component – is:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = \frac{1}{2 T} \cdot {\rm E} \left [ a_\nu ^2 \right ] \cdot |G(f)|^2 \hspace{0.05cm}.$$
Questions
Solution
(2) Due to the lower symbol rate $1/T$,i Quaternary Phase Shift Keying $\rm (QPSK)$ – as well as all related quarternary modulation methods – has a spectrum half as wide as in BPSK ⇒ $f_1\hspace{0.15cm}\underline{ =0.5} \cdot 1/T_{\rm B}$.
(3) The power-spectral density $\rm (PSD)$ of the total signal in the equivalent low-pass range is given by:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) + {\it \Phi}_{s,\hspace{0.05cm} {\rm Q},\hspace{0.05cm} {\rm TP}}(f)= 2 \cdot {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = {1}/{ T} \cdot |G(f)|^2\hspace{0.05cm}.$$
This takes into account, that
- the signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ are uncorrelated sind, such that one can add the PSD components,
- and that the expected value is $E[a_ν^2] = 1$ , due to the binary bipolar amplitude coefficients.
This gives:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{1}{ T} \cdot \left ( \frac {4}{\pi} \right ) ^2 \cdot g_0^2 \cdot T^2 \cdot \frac{ {\rm cos}^2 ( 2 \pi f T )}{ \big [1 - (4 f T)^2 \big ] ^2} \hspace{0.05cm}.$$
With $s_0 = g_0$, $T = T_{\rm B}$ and $E_{\rm B} = s_0^2 · T_{\rm B}/2$ , it further holds that:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{32}{ \pi^2} \cdot E_{\rm B} \cdot \frac{ {\rm cos}^2 ( 2 \pi \cdot f \cdot T_{\rm B} )}{ \big [1 - (4 \cdot f \cdot T_{\rm B})^2 \big ] ^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f = 0 )= \frac{32}{ \pi^2} \cdot E_{\rm B} \hspace{0.15cm}\underline {\approx 3.243 \cdot E_{\rm B}} \hspace{0.05cm}.$$
(4) Only Answer 2 is correct:
- It can already be seen from the graph that the first statement is false and the second is correct.
(𝐸B/𝑇B).
- Answer 3 is also incorrect. The integral over the power-spectral densities yields the power $(E_{\rm B}/T_{\rm B})$.
- The signal waveforms of BPSK, QPSK and MSK make it clear that the power with a constant envelope $(s_0)$ is the same for these three modulation methods.