Difference between revisions of "Aufgaben:Exercise 4.17: Non-Coherent On-Off Keying"
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation}} | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation}} | ||
| − | [[File:P_ID2078__Dig_A_4_17.png|right|frame|Rayleigh and Rice | + | [[File:P_ID2078__Dig_A_4_17.png|right|frame|Rayleigh and Rice PDF]] |
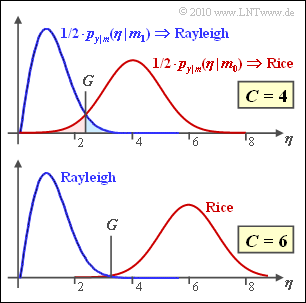
| − | The figure shows the two density functions resulting from a non-coherent demodulation of | + | The figure shows the two density functions resulting from a non-coherent demodulation of "On–Off–Keying" $\rm (OOK)$. It is assumed that the two OOK signal space points are located |
| + | *at $\boldsymbol{s}_0 = C$ $($message $m_0)$ and | ||
| + | |||
| + | *at $\boldsymbol{s}_1 = 0$ $($message $m_1)$. | ||
| + | |||
The symbol error probability of this system is described by the following equation: | The symbol error probability of this system is described by the following equation: | ||
| Line 10: | Line 14: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | With the standard deviation $\sigma_n = 1$, which is assumed in the following, the resulting Rayleigh distribution for $m = m_1$ (blue curve) is: | + | With the standard deviation $\sigma_n = 1$, which is assumed in the following, |
| + | *the resulting Rayleigh distribution for $m = m_1$ (blue curve) is: | ||
:$$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} \hspace{0.05cm}| m_1) = \eta \cdot {\rm e }^{-\eta^2/2} | :$$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} \hspace{0.05cm}| m_1) = \eta \cdot {\rm e }^{-\eta^2/2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | The | + | *The (red) Rice distribution can be approximated in the present case $($because of $C\gg \sigma_n)$ by a Gaussian curve: |
:$$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} |\hspace{0.05cm} m_0) = \frac{1}{\sqrt{2\pi}} \cdot {\rm e }^{-(\eta-C)^2/2} | :$$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} |\hspace{0.05cm} m_0) = \frac{1}{\sqrt{2\pi}} \cdot {\rm e }^{-(\eta-C)^2/2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 20: | Line 25: | ||
The optimal decision boundary $G_{\rm opt}$ is obtained from the intersection of the red and blue curves. | The optimal decision boundary $G_{\rm opt}$ is obtained from the intersection of the red and blue curves. | ||
*From the two sketches it can be seen that $G_{\rm opt}$ depends on $C$. | *From the two sketches it can be seen that $G_{\rm opt}$ depends on $C$. | ||
| − | *For the upper graph $C = 4$, for the lower $C = 6$. | + | |
| + | *For the upper graph $C = 4$, for the lower graph $C = 6$. | ||
| + | |||
*All quantities are normalized and $\sigma_n = 1$ is always assumed. | *All quantities are normalized and $\sigma_n = 1$ is always assumed. | ||
| − | + | Notes: | |
| − | + | * The exercise belongs to the topic of the chapter [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation| "Carrier Frequency Systems with Non-Coherent Demodulation"]]. | |
| − | + | ||
| − | * The exercise belongs to the topic of the chapter [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Non-Coherent_Demodulation| "Carrier Frequency Systems with Non-Coherent Demodulation"]]. | + | * For the complementary Gaussian error integral, you can use the following approximations: |
| − | * For the complementary Gaussian error integral, you can use the following approximations: | ||
:$${\rm Q }(1.5) \approx 0.0668\hspace{0.05cm}, \hspace{0.5cm}{\rm Q }(2.5) \approx 0.0062\hspace{0.05cm}, \hspace{0.5cm} | :$${\rm Q }(1.5) \approx 0.0668\hspace{0.05cm}, \hspace{0.5cm}{\rm Q }(2.5) \approx 0.0062\hspace{0.05cm}, \hspace{0.5cm} | ||
{\rm Q }(2.65) \approx 0.0040 | {\rm Q }(2.65) \approx 0.0040 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * You can check your results with | + | * You can check your results with theHTML5/JavaScript applet [[Applets:Coherent_and_Non-Coherent_On-Off_Keying|"Coherent and Non-coherent On-Off Keying"]]. |
| Line 41: | Line 47: | ||
<quiz display=simple> | <quiz display=simple> | ||
{What is the relationship between the mean symbol energy $E_{\rm S}$ and the constant $C$ of the Rice distribution? | {What is the relationship between the mean symbol energy $E_{\rm S}$ and the constant $C$ of the Rice distribution? | ||
| − | |type=" | + | |type="()"} |
- $E_{\rm S} = C$, | - $E_{\rm S} = C$, | ||
- $E_{\rm S} = C^2$, | - $E_{\rm S} = C^2$, | ||
| − | + $E_{\rm S} = C^2/2$. | + | + $E_{\rm S} = C^2\hspace{-0.1cm}/2$. |
{What is the governing equation for the optimal decision boundary $G_{\rm opt}$? | {What is the governing equation for the optimal decision boundary $G_{\rm opt}$? | ||
| − | |type=" | + | |type="()"} |
- $G = C/2$, | - $G = C/2$, | ||
+ $G \, –1/C \cdot {\rm ln} \, (G) = C/2 + 1/(2C) \cdot {\rm ln} \, (2\pi)$, | + $G \, –1/C \cdot {\rm ln} \, (G) = C/2 + 1/(2C) \cdot {\rm ln} \, (2\pi)$, | ||
| − | - $G | + | - $G = 1/C \cdot {\rm ln} \, (G)$. |
| − | {Determine the optimal decision | + | {Determine the optimal decision threshold for $C = 4$. |
|type="{}"} | |type="{}"} | ||
$G_{\rm opt} \ = \ $ { 2.46 3% } | $G_{\rm opt} \ = \ $ { 2.46 3% } | ||
| − | {What is the symbol error probability | + | {What is the symbol error probability with $C = 4$ and $G = 2.5 \approx G_{\rm opt}$? |
|type="{}"} | |type="{}"} | ||
$p_{\rm S} \ = \ $ { 5.54 3% } $\ \% $ | $p_{\rm S} \ = \ $ { 5.54 3% } $\ \% $ | ||
Revision as of 15:57, 29 August 2022
The figure shows the two density functions resulting from a non-coherent demodulation of "On–Off–Keying" $\rm (OOK)$. It is assumed that the two OOK signal space points are located
- at $\boldsymbol{s}_0 = C$ $($message $m_0)$ and
- at $\boldsymbol{s}_1 = 0$ $($message $m_1)$.
The symbol error probability of this system is described by the following equation:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} | \hspace{0.05cm}m_0) \,{\rm d} \eta +{1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} |\hspace{0.05cm} m_1) \,{\rm d} \eta \hspace{0.05cm}.$$
With the standard deviation $\sigma_n = 1$, which is assumed in the following,
- the resulting Rayleigh distribution for $m = m_1$ (blue curve) is:
- $$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} \hspace{0.05cm}| m_1) = \eta \cdot {\rm e }^{-\eta^2/2} \hspace{0.05cm}.$$
- The (red) Rice distribution can be approximated in the present case $($because of $C\gg \sigma_n)$ by a Gaussian curve:
- $$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} |\hspace{0.05cm} m_0) = \frac{1}{\sqrt{2\pi}} \cdot {\rm e }^{-(\eta-C)^2/2} \hspace{0.05cm}.$$
The optimal decision boundary $G_{\rm opt}$ is obtained from the intersection of the red and blue curves.
- From the two sketches it can be seen that $G_{\rm opt}$ depends on $C$.
- For the upper graph $C = 4$, for the lower graph $C = 6$.
- All quantities are normalized and $\sigma_n = 1$ is always assumed.
Notes:
- The exercise belongs to the topic of the chapter "Carrier Frequency Systems with Non-Coherent Demodulation".
- For the complementary Gaussian error integral, you can use the following approximations:
- $${\rm Q }(1.5) \approx 0.0668\hspace{0.05cm}, \hspace{0.5cm}{\rm Q }(2.5) \approx 0.0062\hspace{0.05cm}, \hspace{0.5cm} {\rm Q }(2.65) \approx 0.0040 \hspace{0.05cm}.$$
- You can check your results with theHTML5/JavaScript applet "Coherent and Non-coherent On-Off Keying".
Questions
Solution
- The energy is equal to the value $\boldsymbol{s}_0 = C$ in the signal space constellation squared, divided by $2$.
- The factor $1/2$ takes into account that the message $m_1$ does not contribute any energy ($\boldsymbol{s}_1 = 0$).
(2) Solution 2 is correct here:
- The optimal decision boundary $G$ lies at the intersection of the two curves shown.
- The factor $1/2$ considers the equally probable messages $m_0$ and $m_1$. Thus, the following determination equation is obtained:
- $${G}/{2} \cdot {\rm exp } \left [ - {G^2 }/{2 }\right ] = \frac{1}{2 \cdot \sqrt{2\pi}} \cdot {\rm exp } \left [ - \frac{G^2 - 2 C \cdot G + C^2}{2 }\right ]$$
- $$\Rightarrow \hspace{0.3cm} \sqrt{2\pi} \cdot G = {\rm exp } \left [ C \cdot G - C^2/2 \right ] \hspace{0.3cm}\Rightarrow \hspace{0.3cm} C \cdot G - {\rm ln }\hspace{0.15cm} (\sqrt{2\pi} \cdot G) - C^2/2 = 0$$
- $$\Rightarrow \hspace{0.3cm} G - {1}/{C} \cdot {\rm ln }\hspace{0.15cm} ( G) = C/2 + {1}/({2C}) \cdot {\rm ln }\hspace{0.15cm} (\sqrt{2\pi}) = C/2 + {1}/({2C}) \cdot {\rm ln }\hspace{0.15cm} ({2\pi})\hspace{0.05cm}.$$
(3) With $C = 4$, the governing equation given in (2) is
- $$f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} G - {1}/{C} \cdot {\rm ln }\hspace{0.15cm} ( G) - C/2 - {1}/({2C}) \cdot {\rm ln }\hspace{0.15cm} ({2\pi})= G - 0.25 \cdot {\rm ln }\hspace{0.15cm} ( G) - 2 - {\rm ln }\hspace{0.15cm} ({2\pi})/8 \approx G - 0.25 \cdot {\rm ln }\hspace{0.15cm} ( G) - 2.23 = 0 \hspace{0.05cm}.$$
- This equation can only be solved numerically:
- $$G = 2.0\text{:}\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.403 \hspace{0.05cm}, \hspace{0.2cm}G = 3.0\text{:}\hspace{0.15cm}f(G) = 0.495 \hspace{0.05cm}, \hspace{0.2cm}G = 2.5\text{:}\hspace{0.15cm}f(G) = 0.041\hspace{0.05cm},$$
- $$ G = 2.4\text{:}\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.049 \hspace{0.05cm}, \hspace{0.2cm}G = 2.46\text{:}\hspace{0.15cm}f(G) \approx 0 \hspace{0.05cm}.$$
- Thus, the optimal decider boundary is $G_{\rm opt} \underline {= 2.46 \approx 2.5}$.
(4) The error probability is composed of two parts:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot {\rm Pr}({\cal{E}}\hspace{0.05cm}| \hspace{0.05cm} m = m_1)+{1}/{ 2}\cdot {\rm Pr}({\cal{E}}\hspace{0.05cm}| \hspace{0.05cm} m = m_0)\hspace{0.05cm}.$$
- The first part (falsification from $m_1$ nach $m_0$) results from the crossing of the limit $G$ by the Rayleigh distribution
- $${\rm Pr}({\cal{E}} \hspace{0.05cm}| \hspace{0.05cm} m = m_1) = \int_{G}^{\infty} p_{y\hspace{0.05cm}| \hspace{0.05cm}m} (\eta \hspace{0.05cm}| \hspace{0.05cm} m_1) \,{\rm d} \eta = {\rm e }^{-G^2/2}= {\rm e }^{-3.125}\approx 0.044 \hspace{0.05cm}.$$
- The second part (falsification from $m_0$ to $m_1$) results from the Rice distribution, which is approximated here by the Gaussian distribution:
- $${\rm Pr}({\cal{E}}| m = m_0) = \int_{0}^{G} p_{y\hspace{0.05cm}| \hspace{0.05cm}m} (\eta \hspace{0.05cm}| \hspace{0.05cm} m_0) \,{\rm d} \eta = \frac{1}{\sqrt{2\pi}} \cdot \int_{0}^{G} {\rm e }^{-(\eta-C)^2/2} \,{\rm d} \eta \hspace{0.05cm}.$$
- This part can be given by the complementary Gaussian error integral ${\rm Q}(x)$:
- $${\rm Pr}({\cal{E}}\hspace{0.05cm}| \hspace{0.05cm} m = m_0) = {\rm Pr}(y < G-C) = {\rm Pr}(y > C-G) = {\rm Q }(\frac{C-G}{\sigma_n})= {\rm Q }(\frac{4-2.5}{1})= {\rm Q }(1.5) \approx 0.0688 \hspace{0.05cm}. $$
- This gives a total of:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot 0.0440 +{1}/{ 2} \cdot 0.0668 \approx \underline{5.54\, \%}\hspace{0.05cm}.$$
Note: A system simulation has shown that a slightly smaller error probability results if the actual Rice distribution is used instead of the Gaussian approximation. Then with $G = 2.5$:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot 0.0440 + {1}/{ 2} \cdot 0.0484 \approx \underline{4.62\, \%}\hspace{0.05cm}.$$
Thus, the Gaussian approximation provides an upper bound on the true error probability.
(5) With $C = 6$, the governing equation given in (3) is
- $$f(G)= G - {1}/{C} \cdot {\rm ln }\hspace{0.15cm} ( G) - C/2 - \frac{1}{2C} \cdot {\rm ln }\hspace{0.15cm} ({2\pi}) \approx G - {\rm ln }\hspace{0.15cm} ( G)/6 - 3.153 = 0 \hspace{0.05cm},$$
- $$G = 3.0\hspace{-0.1cm}:\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.336 \hspace{0.05cm}, \hspace{0.2cm}G = 3.50\hspace{-0.1cm}:\hspace{0.15cm}f(G) = 0.138 \hspace{0.05cm},$$
- $$ G = 3.3\hspace{-0.1cm}:\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.052 \hspace{0.05cm}, \hspace{0.2cm}G = 3.35\hspace{-0.1cm}:\hspace{0.15cm}f(G) \approx 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{G_{\rm opt} \approx 3.35}\hspace{0.05cm}.$$
(6) Analogous to subtask (4), we obtain with $G = 3.5$:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot {\rm e }^{-G^2/2} +{1}/{ 2} \cdot {\rm Q }(C-G)= {1}/{ 2} \cdot {\rm e }^{-6.125} + {1}/{ 2} \cdot {\rm Q }(2.5)= {1}/{ 2} \cdot 2.2 \cdot 10^{-3} + {1}/{ 2} \cdot 6.2 \cdot 10^{-3} \underline{= 0.42 \,\%} \hspace{0.05cm}.$$
- For $C = 6$, the optimal decision boundary ($G_{\rm opt} = 3.35$) results in an error probability that is about a factor of $10$ smaller than with $C = 4$:
- $$p_{\rm S} = {1}/{ 2} \cdot {\rm e }^{-5.61} + {1}/{ 2} \cdot {\rm Q }(2.65)= {1}/{ 2} \cdot 3.6 \cdot 10^{-3} +{1}/{ 2} \cdot 4 \cdot 10^{-3}= {0.38 \,\%} \hspace{0.05cm}.$$
- The actual error probability using the Rice distribution (no Gaussian approximation) gives a slightly smaller value: $0.33\%$.