Difference between revisions of "Aufgaben:Exercise 4.17Z: Rayleigh and Rice Distribution"
| Line 16: | Line 16: | ||
In dieser Gleichung bezeichnet ${\rm I}_0(x)$ die [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation#Rayleigh.E2.80.93_und_Riceverteilung| modifizierte Besselfunktion nullter Ordnung]]. | In dieser Gleichung bezeichnet ${\rm I}_0(x)$ die [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation#Rayleigh.E2.80.93_und_Riceverteilung| modifizierte Besselfunktion nullter Ordnung]]. | ||
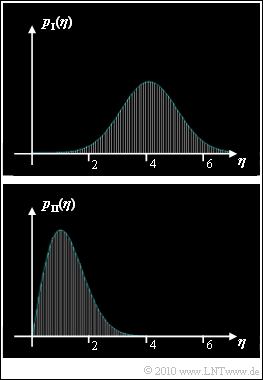
| − | In der Grafik sind die beiden Dichtefunktionen dargestellt, wobei allerdings nicht angegeben wird, ob $p_{\rm I}(\eta)$ bzw. $p_{\rm II}(\eta)$ der Riceverteilung zuordnen, und für die Ermittlung der WDF–Parameter können Sie folgende Aussagen berücksichtigen: | + | In der Grafik sind die beiden Dichtefunktionen dargestellt, wobei allerdings nicht angegeben wird, ob $p_{\rm I}(\eta)$ bzw. $p_{\rm II}(\eta)$ zu einer Rayleigh– oder zu einer Riceverteilung gehören. Bekannt ist nur, dass je eine Rayleigh– und eine Riceverteilung dargestellt ist. Der Parameter $\sigma_$ ist bei beiden gleich. |
| + | |||
| + | Für Ihre Entscheidung, ob Sie $p_{\rm I}(\eta)$ oder $p_{\rm II}(\eta)$ der Riceverteilung zuordnen, und für die Ermittlung der WDF–Parameter können Sie folgende Aussagen berücksichtigen: | ||
* Für große Werte des Quotienten $C/\sigma_n$ lässt sich die Riceverteilung durch eine Gaußverteilung mit Mittelwert $C$ und Streuung $\sigma_n$ annähern. | * Für große Werte des Quotienten $C/\sigma_n$ lässt sich die Riceverteilung durch eine Gaußverteilung mit Mittelwert $C$ und Streuung $\sigma_n$ annähern. | ||
| − | * Die der Grafik zugrunde liegenden Werte von $C$ und $\sigma_n$ sind ganzzahlig | + | * Die der Grafik zugrunde liegenden Werte von $C$ und $\sigma_n$ sind ganzzahlig. |
| + | |||
| + | |||
| + | Hinsichtlich der Rayleighverteilung ist zu beachten: | ||
| + | * Für beide Verteilungen ist das gleiche $\sigma_n$ zugrunde gelegt. | ||
| + | * Für die Streuung (Wurzel aus der Varianz) der Rayleighverteilung gilt: | ||
| + | :$$\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n | ||
| + | \hspace{0.05cm}.$$ | ||
| + | * Für die Streuung/Varianz der Riceverteilung kann allgemein nur ein komplizierter Ausdruck mit hypergeometrischen Funktionen angegeben werden, ansonsten nur eine Näherung für $C >> \sigma_n$ entsprechend der Gaußverteilung. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Diese Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation| Trägerfrequenzsysteme mit nichtkohärenter Demodulation]]. | ||
| + | * Gegeben ist zudem das folgende Integral: | ||
| + | :$$\int x \cdot {\rm e }^{-x^2} \,{\rm d} x = | ||
| + | -{1}/{2} \cdot {\rm e }^{-x^2} + {\rm const. } $$ | ||
| + | |||
Revision as of 10:53, 11 November 2017
Für die Untersuchung von Nachrichtensystemen haben die Rayleigh– und die Rice–Verteilung eine große Bedeutung. Im Folgenden sei $y$ eine rayleigh– oder eine riceverteilte Zufallsgröße und $\eta$ jeweils eine Realisierung davon.
- Die Rayleighverteilung ergibt sich dabei für die Wahrscheinlichkeitsdichtefunktion (kurz: WDF) einer Zufallsgröße $y$, die sich aus den beiden gaußverteilten und statistisch unabhängigen Komponenten $u$ und $\upsilon$ (beide mit der Streuung $\sigma_n$) wie folgt ergibt:
- $$y = \sqrt{u^2 + v^2} \hspace{0.1cm} \Rightarrow \hspace{0.1cm} p_y (\eta) = \frac{\eta}{\sigma_n^2} \cdot {\rm exp } \left [ - \frac{\eta^2}{2 \sigma_n^2}\right ] \hspace{0.01cm}.$$
- Die Riceverteilung erhält man unter sonst gleichen Randbedingungen für den Anwendungsfall, dass bei einer der beiden Komponenten noch eine Konstante $C$ addiert wird:
- $$y = \sqrt{(u+C)^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) = \frac{\eta}{\sigma_n^2} \cdot {\rm exp } \left [ - \frac{\eta^2 + C^2}{2 \sigma_n^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta \cdot C}{ \sigma_n^2}\right ] \hspace{0.05cm}.$$
In dieser Gleichung bezeichnet ${\rm I}_0(x)$ die modifizierte Besselfunktion nullter Ordnung.
In der Grafik sind die beiden Dichtefunktionen dargestellt, wobei allerdings nicht angegeben wird, ob $p_{\rm I}(\eta)$ bzw. $p_{\rm II}(\eta)$ zu einer Rayleigh– oder zu einer Riceverteilung gehören. Bekannt ist nur, dass je eine Rayleigh– und eine Riceverteilung dargestellt ist. Der Parameter $\sigma_$ ist bei beiden gleich.
Für Ihre Entscheidung, ob Sie $p_{\rm I}(\eta)$ oder $p_{\rm II}(\eta)$ der Riceverteilung zuordnen, und für die Ermittlung der WDF–Parameter können Sie folgende Aussagen berücksichtigen:
- Für große Werte des Quotienten $C/\sigma_n$ lässt sich die Riceverteilung durch eine Gaußverteilung mit Mittelwert $C$ und Streuung $\sigma_n$ annähern.
- Die der Grafik zugrunde liegenden Werte von $C$ und $\sigma_n$ sind ganzzahlig.
Hinsichtlich der Rayleighverteilung ist zu beachten:
- Für beide Verteilungen ist das gleiche $\sigma_n$ zugrunde gelegt.
- Für die Streuung (Wurzel aus der Varianz) der Rayleighverteilung gilt:
- $$\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n \hspace{0.05cm}.$$
- Für die Streuung/Varianz der Riceverteilung kann allgemein nur ein komplizierter Ausdruck mit hypergeometrischen Funktionen angegeben werden, ansonsten nur eine Näherung für $C >> \sigma_n$ entsprechend der Gaußverteilung.
Hinweise:
- Diese Aufgabe gehört zum Kapitel Trägerfrequenzsysteme mit nichtkohärenter Demodulation.
- Gegeben ist zudem das folgende Integral:
- $$\int x \cdot {\rm e }^{-x^2} \,{\rm d} x = -{1}/{2} \cdot {\rm e }^{-x^2} + {\rm const. } $$
Fragebogen
Musterlösung