Exercise 4.18: Non-Coherent FSK Demodulation

From LNTwww
Revision as of 17:01, 16 August 2022 by Hwang (talk | contribs)

Non-coherent demodulation

We consider Frequency Shift Keying  (FSK) with  $M = 2$   ⇒   binary signaling. The two low-pass basis functions in this case are complex and are:

$$\xi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$
$$ \xi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.$$

Then, for the two possible waveforms in the low-pass region, with the mean symbol energy  $E_{\rm S}$:

$$m_0\text{:}\hspace{0.2cm} s_{\rm TP,\hspace{0.05cm}0} = \sqrt{E_{\rm S}} \cdot \xi_1(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 0} = (\sqrt{E_{\rm S}}, 0)\hspace{0.05cm},$$
$$m_1\text{:}\hspace{0.2cm} s_{\rm TP,\hspace{0.05cm}1} = \sqrt{E_{\rm S}} \cdot \xi_2(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 1} = (0, \sqrt{E_{\rm S}})\hspace{0.05cm}.$$

Here,  $h$  indicates the so-called modulation index. This must meet certain criteria to result in orthogonal waveforms. However, these criteria depend on whether a coherent or a non-coherent demodulator is used at the receiver.

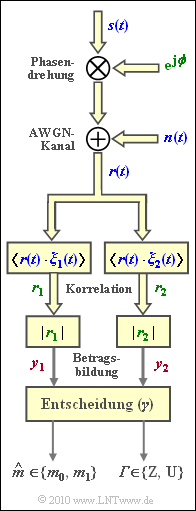
The diagram shows the non-coherent demodulator for binary Frequency Shift Keying  (FSK) in the lower section. All complex signals are labeled in blue, complex values in green, and real values in red.

Compared to the decision process given in the  "theory part",  we now consider a complex decision that outputs a safety flag  ${\it \Gamma} = \{{\rm Z}, \ {\rm U}\}$  in addition to the estimated value. The logical values  ${\rm Z}$  and  ${\rm U}$  stand for a realiable (Zuverlässige) and an Unreliable decision, respectively. Thus, there are four possibilities for the decision, controlled by the parameter  $\gamma$:

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_0,\hspace{0.05cm}{\it \Gamma} = {\rm Z}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_1 > \gamma \cdot y_2\hspace{0.05cm},$$
$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_0,\hspace{0.05cm}{\it \Gamma} = {\rm U}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_2 < y_1 < \gamma \cdot y_2\hspace{0.05cm},$$
$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_1,\hspace{0.05cm}{\it \Gamma} = {\rm Z}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_2 > \gamma \cdot y_1\hspace{0.05cm},$$
$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_1,\hspace{0.05cm}{\it \Gamma} = {\rm U}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_1 < y_2 < \gamma \cdot y_1\hspace{0.05cm}.$$

In the questions for the exercise, the two values  $\gamma = 1$  and  $\gamma = 2$  are considered.

For the probability that the decision erroneously chooses the symbol  $m_1$  and, moreover, indicates that this decision is to be considered reliable (particularly reprehensible), the following applies

$${\rm Pr}\{\hat{m} = m_1,\hspace{0.05cm}{\it \Gamma} = {\rm Z} \hspace{0.05cm}| \hspace{0.05cm}m_0 \} = \frac{1}{1 + \gamma^2} \cdot {\rm exp } \left [ - \frac{\gamma^2 \cdot E_{\rm S}}{(1+\gamma^2) \cdot N_{\rm 0}}\right ] \hspace{0.05cm}.$$



Note:



Fragebogen

1

Welche Aussagen sind bei kohärenter Demodulation der FSK zutreffend?

Orthogonalität ergibt sich, wenn  $h$  ganzzahlig ist.
Auch für  $h = 0.5$  ergeben sich orthogonale Signalformen.
Orthogonalität ist grundsätzlich nicht zu erreichen.
Beim AWGN–Kanal gilt  $r(t) = s(t) + n(t)$.

2

Welche Aussagen sind bei nichtkohärenter Demodulation der FSK zutreffend?

Orthogonalität ergibt sich, wenn  $h$  ganzzahlig ist.
Auch für  $h = 0.5$  ergeben sich orthogonale Signalformen.
Orthogonalität ist grundsätzlich nicht zu erreichen.
Beim AWGN–Kanal gilt  $r(t) = s(t) + n(t)$.

3

Es sei  $E_{\rm S}/N_0 = 10$. Wie groß ist die Fehlerwahrscheinlichkeit, also die Wahrscheinlichkeit, dass der Schätzwert von der gesendeten Nachricht abweicht?

$p_{\rm S} \ = \ $

$\ \%$

4

Es sei  $\gamma = 2$  und  $E_{\rm S}/N_0 = 10$. Wie groß ist die Wahrscheinlichkeit, dass trotz Fehler das Sicherheitsflag eine zuverlässige Entscheidung signalisiert?

${\rm Pr}({\it \Gamma} = {\rm Z\hspace{0.05cm} | \hspace{0.05cm}Fehler}) \ = \ $

$\ \cdot 10^{\rm –5}$

5

Es sei weiterhin  $\gamma = 2$ und  $E_{\rm S}/N_0 = 10$. Wie groß ist die (bedingte) Wahrscheinlichkeit, dass bei einem Fehler die Zusatzinformation "unzuverlässig" angezeigt wird?

${\rm Pr}({\it \Gamma} = {\rm U\hspace{0.05cm} | \hspace{0.05cm}Fehler}) \ = \ $

$\ \%$


Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschlag 1, 2 und 4:

  • Bei kohärenter Demodulation ist Orthogonalität dann gegeben, wenn der Modulationsindex $h$ ein Vielfaches von $0.5$ ist. Binäre FSK mit $h = 0.5$ nennt man auch Minimum Shift Keying (MSK).
  • Da durch die Phasenregelung die Phasenverschiebung (Laufzeit) auf dem AWGN–Übertragungskanal ausgeglichen wird   ⇒   ${\rm e}^{{\rm j}\phi} \cdot {\rm e}^{-{\rm j}\phi} = 1$, gilt tatsächlich für die Signale im äquivalenten Tiefpassbereich:   $r(t) = s(t) + n(t) \hspace{0.05cm}.$


(2)  Hier ist nur der erste Lösungsvorschlag richtig, das heißt, es muss nun $h = 1, \ 2, \ 3, \text{ ...}$ ganzzahlig sein.

  • Nichtkohärente Demodulation von FSK ist somit nicht möglich.
  • Wegen der fehlenden Phasenregelung gilt außerdem:
$$r(t) = s(t) \cdot {\rm e }^{ - {\rm j }\hspace{0.05cm}\phi} + n(t) \hspace{0.05cm}.$$


(3)  Bei gleichwahrscheinlichen Nachrichten gilt:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Pr}({\cal{E}}| \hspace{0.05cm}m = m_0) = {\rm Pr}(\hat{m}= m_1| \hspace{0.05cm}m = m_0)\hspace{0.05cm}.$$
  • Diese Wahrscheinlichkeit ergibt sich aus der vorgegebenen Gleichung mit $\gamma = 1$.
  • In diesem Fall ist stets ${\it \Gamma} ={\rm Z}$ und die Entscheidungsregel lautet:   Entscheide auf das Symbol $m_0$, falls $y_1 > y_2$.
  • Daraus folgt:
$$p_{\rm S} = \frac{1}{1 + \gamma^2} \cdot {\rm exp } \left [ - \frac{\gamma^2 \cdot E_{\rm S}}{(1+\gamma^2) \cdot N_{\rm 0}}\right ]_{\gamma = 1} = {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)}\hspace{0.05cm}.$$
  • Mit $E_{\rm S}/N_0 = 10$ erhält man $p_{\rm S} = 1/2 \cdot {\rm e}^{\rm –5} \approx \underline {0.337 \cdot \%}$.


(4)  Diese Wahrscheinlichkeit ergibt sich aus Symmetriegründen zu

$${\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) = {1}/{2} \cdot {\rm Pr}\{(\hat{m} = m_1)\hspace{0.05cm}\cap\hspace{0.05cm}{\it \Gamma} = {\rm Z} \hspace{0.05cm}| \hspace{0.05cm}m_0 \} + {1}/{2}\cdot {\rm Pr}\{(\hat{m} = m_0)\hspace{0.05cm}\cap\hspace{0.05cm}({\it \Gamma} = {\rm Z}) \hspace{0.05cm}| \hspace{0.05cm}m_1 \} $$
$$\Rightarrow \hspace{0.3cm} {\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) = {\rm Pr}\{(\hat{m} = m_1)\hspace{0.05cm}\cap\hspace{0.05cm}({\it \Gamma} = {\rm Z}) \hspace{0.05cm}| \hspace{0.05cm}m_0 \} =\frac{1}{1 + 2^2} \cdot {\rm exp } \left [ - \frac{2^2 \cdot E_{\rm S}}{(1+2^2) \cdot N_{\rm 0}}\right ] = {1}/{5} \cdot {\rm e }^{-8} = \underline{6.7 \cdot 10^{-5}}\hspace{0.05cm}.$$


(5)  Da ${\rm U}$ und ${\rm Z}$ nach der Statistik ein vollständiges System ergeben, gilt mit den Ergebnissen der Teilaufgaben (3) und (4):

$${\rm Pr}({\it \Gamma} = {\rm U}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) ={\rm Pr}( {\rm Fehler} ) - {\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) = 3.37 \cdot 10^{-3} - 6.7 \cdot 10^{-5} = \underline{3.3 \cdot 10^{-3}} \hspace{0.05cm}.$$
  • Damit ist die gesuchte bedingte Wahrscheinlichkeit ${\rm Pr}({\it \Gamma}= {\rm U}\hspace{0.05cm}|\hspace{0.05cm} {\rm Fehler})$:
$${\rm Pr}({\it \Gamma}= {\rm U}\hspace{0.05cm}|\hspace{0.05cm} {\rm Fehler} ) = \frac{{\rm Pr}({\it \Gamma} = {\rm U}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm Fehler} ) }{{\rm Pr}( {\rm Fehler} )} = \frac{3.3 \cdot 10^{-3}}{3.37 \cdot 10^{-3}} \hspace{0.15cm} \underline{= 98 \%} \hspace{0.05cm}.$$

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_4.18:_Non-Coherent_FSK_Demodulation&oldid=48400"
  • Powered by MediaWiki