Difference between revisions of "Aufgaben:Exercise 4.1: Triangular (x, y) Area"
| (19 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables |
}} | }} | ||
| − | [[File:P_ID172__Sto_A_4_1.png|right| | + | [[File:P_ID172__Sto_A_4_1.png|right|frame|Triangular two-dimensional area]] |
| − | + | A two-dimensional random variable is defined by the adjacent sketch: | |
| + | *For $(x, \ y)$ only values within the triangular-shaped region defined by the three vertices $(0,\ 1)$,$ $(4,\ 3)$,$ and $(4,\ 5)$ can occur. | ||
| + | *Within the triangle, all the random variables $(x,\ y)$ are equally probable. | ||
| + | *For the 2D–PDF, in this domain: | ||
:$$f_{xy}(x,y) = A .$$ | :$$f_{xy}(x,y) = A .$$ | ||
| − | + | In addition, the straight line $x = y$ ⇒ "angle bisector" is drawn in the graphic ⇒ see subtask '''(2)'''. | |
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | Hint: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables|Two-Dimensional Random Variables]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the PDF constant using geometric considerations. |
|type="{}"} | |type="{}"} | ||
| − | $A \ =$ { 0.25 3% } | + | $A \ = \ $ { 0.25 3% } |
| − | { | + | {Calculate the probability that $x$ is greater than $y$. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(x > y) \ =$ { 0.25 3% } | + | ${\rm Pr}(x > y) \ = \ $ { 0.25 3% } |
| − | { | + | {Determine the marginal PDF $f_x(x)$. Calculate the probability that $x$ is greater than or equal to $2$. <br>Check the value with the 2D–PDF. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(x ≥ 2)\ =$ { 0.75 3% } | + | ${\rm Pr}(x ≥ 2)\ = \ $ { 0.75 3% } |
| − | { | + | {Determine the marginal PDF $f_y(y)$. Calculate the probability that $y$ is greater than or equal to $3$. <br>Check the value with the 2D–PDF. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(y ≥ 3)\ =$ { 0.5 3% } | + | ${\rm Pr}(y ≥ 3)\ = \ $ { 0.5 3% } |
| − | { | + | {What is the probability that the random variable $x$ is greater than or equal to $2$ and at the same time the random variable $y$ is greater than or equal to $3$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}[(x ≥ 2) ∩ (y ≥ 3)]\ =$ { 0.5 3% } | + | ${\rm Pr}\big[(x ≥ 2) ∩ (y ≥ 3)\big]\ = \ $ { 0.5 3% } |
| − | { | + | {What is the probability that $x$ is greater than or equal to $2$ given $y \ge 3$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}[x ≥ 2 | y ≥ 3]\ =$ { 1 3% } | + | ${\rm Pr}\big[x ≥ 2\hspace{0.05cm} | \hspace{0.05cm} y ≥ 3\big]\ = \ $ { 1 3% } |
| − | { | + | {What is the probability that $y \ge 3$ given that $x \ge 2$ holds? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}[y ≥ 3 | x ≥ 2]\ =$ { 0.667 3% } | + | ${\rm Pr}\big[y ≥ 3\hspace{0.05cm} | \hspace{0.05cm} x ≥ 2\big]\ = \ $ { 0.667 3% } |
| − | |||
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' The volume under the two dimensional PDF is by definition equal to $1$: | |
| + | [[File:P_ID219__Sto_A_4_1_b.png|right|frame|Triangular 2D–PDF]] | ||
:$$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x\, {\rm d}y=1.$$ | :$$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x\, {\rm d}y=1.$$ | ||
| − | + | *The triangle area is $D = 0.5 \cdot 2 \cdot 4 = 4$. | |
| − | + | *Since in this definition area the PDF is constantly equal to $A$, we get. | |
| + | :$$A= 1/D\hspace{0.15cm}\underline{= 0.25}.$$ | ||
| − | |||
| − | + | '''(2)''' For the solution we start from the adjacent sketch. | |
| + | *The area $x>y$ lies to the right of the angle bisector $x=y$ and is marked in green. | ||
| + | *This green triangular area is $D_{\rm (2)} = 0.5 \cdot 1 \cdot 2 = 1 $, i.e. exactly one quarter of the total area $D$ of the definition area. | ||
| + | *From this follows ${\rm Pr}(x > y)\hspace{0.15cm}\underline{= 0.25}$. | ||
| − | + | ||
| + | |||
| + | '''(3)''' For the wanted marginal PDF holds in this case: | ||
| + | [[File:P_ID220__Sto_A_4_1_c.png|right|frame|Marginal PDF with respect to $x$]] | ||
:$$f_x(x)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}y=A\cdot B_y (x).$$ | :$$f_x(x)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}y=A\cdot B_y (x).$$ | ||
| − | + | *Here denotes $B_y(x)$ the width of the area $f_{xy} \ne 0$ in $y$–direction at the considered $x$–value. | |
| − | + | *It holds: $B_y(x) = x/2$. With $A = 0.25$ it follows $f_{x}(x) = x/8$ for the range $ 0 \le x \le 4$. | |
| − | |||
| − | |||
| − | : | + | *The wanted probability corresponds to the shaded area in the accompanying sketch. One obtains: |
| − | + | :$$\rm Pr(\it x\ge \rm 2) = \rm 1-\rm Pr(\it x < \rm 2) = \rm 1-\frac{1}{2}\cdot2\cdot 0.25\hspace{0.15cm}\underline{ =0.75}. $$ | |
| − | : | + | *The same result is obtained using 2D–PDF: To the right of $x = 2$ lies $3/4$ of the total definition area. |
| + | <br clear=all> | ||
| + | [[File:P_ID221__Sto_A_4_1_d.png|right|frame|Marginal PDF with respect to $y$]] | ||
| + | '''(4)''' Analogous to the solution of the subtask '''(3)''' holds: | ||
:$$f_y(y)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x=A\cdot B_x (y).$$ | :$$f_y(y)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x=A\cdot B_x (y).$$ | ||
| − | + | *The width of PDF area in $x$–direction is zero for $y \le 1$ and $y \ge 5$ respectively. | |
| + | *The maximum is at $y=3$ and gives $B_x(y=3) = 2$. | ||
| + | *In between, the increase and decrease of $B_x(y)$ is linear, yielding a triangular-shaped PDF. | ||
| + | *The probability that $y=3$ corresponds to the green shaded area in the adjacent sketch. | ||
| + | * Because of the symmetry, one obtains: | ||
| + | :$${\rm Pr}(y ≥ 3)\hspace{0.15cm}\underline{ =0.5}. $$ | ||
| + | |||
| + | The same result is obtained using 2D–PDF: Above the horizontal $y= 3$ lies half of the total definition area. | ||
| + | |||
| + | |||
| + | |||
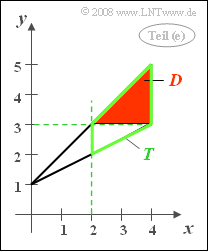
| + | [[File:P_ID222__Sto_A_4_1_e.png|right|frame|On subtask '''(5)''']] | ||
| + | '''(5)''' If $y \ge 3$ $($red highlighted triangle $D)$, it is always true $x \ge 2$ $($green outlined trapezoid $T)$. | ||
| + | *This means: In this example $D$ is a subset of $T$, and it holds: | ||
| + | :$${\rm Pr}[(x ≥ 2) ∩ (y ≥ 3)] = {\rm Pr}(y ≥ 3) \hspace{0.15cm}\underline{= 0.50}.$$ | ||
| + | |||
| + | |||
| − | + | '''(6)''' According to the solution to the subtask '''(5)''', it follows from $y \ge 3$ with certainty also $x \ge 2$. | |
| − | [ | + | *So the conditional probability we are looking for is: |
| + | :$${\rm Pr}[x ≥ 2\hspace{0.05cm} | \hspace{0.05cm} y ≥ 3]\hspace{0.15cm}\underline{= 1}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(7)''' This subtask can be solved using Bayes' theorem and the results from '''(2)''' and '''(5)''': | |
| − | :$$\rm Pr(\it y \ge \rm 3\hspace{0.1cm}|\hspace{0.1cm} \it x \ge \rm 2) = \frac{ \rm Pr((\it x \ge \rm 2)\cap(\it y \ge \rm 3))} {\rm Pr(\it x \ge \rm 2)}\hspace{0.15cm}\underline{= | + | :$$\rm Pr(\it y \ge \rm 3\hspace{0.1cm}|\hspace{0.1cm} \it x \ge \rm 2) = \frac{ \rm Pr((\it x \ge \rm 2)\cap(\it y \ge \rm 3))} {\rm Pr(\it x \ge \rm 2)}=2/3\hspace{0.15cm}\underline{=0.667}.$$ |
| − | : | + | * Or expressed differently: The area $D$ of the triangle with red background makes $2/3$ of the area of the trapezoid with green border $T$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^4.1 Two-Dimensional Random Variables^]] |
Latest revision as of 13:05, 7 February 2022
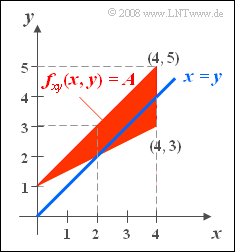
A two-dimensional random variable is defined by the adjacent sketch:
- For $(x, \ y)$ only values within the triangular-shaped region defined by the three vertices $(0,\ 1)$,$ $(4,\ 3)$,$ and $(4,\ 5)$ can occur.
- Within the triangle, all the random variables $(x,\ y)$ are equally probable.
- For the 2D–PDF, in this domain:
- $$f_{xy}(x,y) = A .$$
In addition, the straight line $x = y$ ⇒ "angle bisector" is drawn in the graphic ⇒ see subtask (2).
Hint:
- The exercise belongs to the chapter Two-Dimensional Random Variables.
Questions
Solution
- $$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x\, {\rm d}y=1.$$
- The triangle area is $D = 0.5 \cdot 2 \cdot 4 = 4$.
- Since in this definition area the PDF is constantly equal to $A$, we get.
- $$A= 1/D\hspace{0.15cm}\underline{= 0.25}.$$
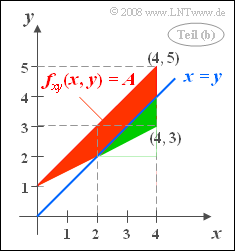
(2) For the solution we start from the adjacent sketch.
- The area $x>y$ lies to the right of the angle bisector $x=y$ and is marked in green.
- This green triangular area is $D_{\rm (2)} = 0.5 \cdot 1 \cdot 2 = 1 $, i.e. exactly one quarter of the total area $D$ of the definition area.
- From this follows ${\rm Pr}(x > y)\hspace{0.15cm}\underline{= 0.25}$.
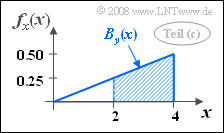
(3) For the wanted marginal PDF holds in this case:
- $$f_x(x)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}y=A\cdot B_y (x).$$
- Here denotes $B_y(x)$ the width of the area $f_{xy} \ne 0$ in $y$–direction at the considered $x$–value.
- It holds: $B_y(x) = x/2$. With $A = 0.25$ it follows $f_{x}(x) = x/8$ for the range $ 0 \le x \le 4$.
- The wanted probability corresponds to the shaded area in the accompanying sketch. One obtains:
- $$\rm Pr(\it x\ge \rm 2) = \rm 1-\rm Pr(\it x < \rm 2) = \rm 1-\frac{1}{2}\cdot2\cdot 0.25\hspace{0.15cm}\underline{ =0.75}. $$
- The same result is obtained using 2D–PDF: To the right of $x = 2$ lies $3/4$ of the total definition area.
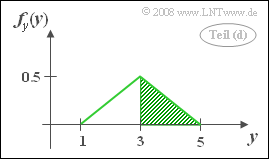
(4) Analogous to the solution of the subtask (3) holds:
- $$f_y(y)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x=A\cdot B_x (y).$$
- The width of PDF area in $x$–direction is zero for $y \le 1$ and $y \ge 5$ respectively.
- The maximum is at $y=3$ and gives $B_x(y=3) = 2$.
- In between, the increase and decrease of $B_x(y)$ is linear, yielding a triangular-shaped PDF.
- The probability that $y=3$ corresponds to the green shaded area in the adjacent sketch.
- Because of the symmetry, one obtains:
- $${\rm Pr}(y ≥ 3)\hspace{0.15cm}\underline{ =0.5}. $$
The same result is obtained using 2D–PDF: Above the horizontal $y= 3$ lies half of the total definition area.
(5) If $y \ge 3$ $($red highlighted triangle $D)$, it is always true $x \ge 2$ $($green outlined trapezoid $T)$.
- This means: In this example $D$ is a subset of $T$, and it holds:
- $${\rm Pr}[(x ≥ 2) ∩ (y ≥ 3)] = {\rm Pr}(y ≥ 3) \hspace{0.15cm}\underline{= 0.50}.$$
(6) According to the solution to the subtask (5), it follows from $y \ge 3$ with certainty also $x \ge 2$.
- So the conditional probability we are looking for is:
- $${\rm Pr}[x ≥ 2\hspace{0.05cm} | \hspace{0.05cm} y ≥ 3]\hspace{0.15cm}\underline{= 1}.$$
(7) This subtask can be solved using Bayes' theorem and the results from (2) and (5):
- $$\rm Pr(\it y \ge \rm 3\hspace{0.1cm}|\hspace{0.1cm} \it x \ge \rm 2) = \frac{ \rm Pr((\it x \ge \rm 2)\cap(\it y \ge \rm 3))} {\rm Pr(\it x \ge \rm 2)}=2/3\hspace{0.15cm}\underline{=0.667}.$$
- Or expressed differently: The area $D$ of the triangle with red background makes $2/3$ of the area of the trapezoid with green border $T$.