Difference between revisions of "Aufgaben:Exercise 4.1Z: Log Likelihood Ratio at the BEC Model"
m (Guenter verschob die Seite 4.1Z L–Werte des BEC–Modells nach Aufgabe 4.1Z: L–Werte des BEC–Modells) |
|||
| Line 3: | Line 3: | ||
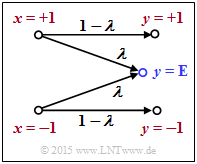
[[File:P_ID2978__KC_Z_4_1.png|right|frame|BEC–Kanalmodell]] | [[File:P_ID2978__KC_Z_4_1.png|right|frame|BEC–Kanalmodell]] | ||
Wir betrachten das so genannte [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| BEC–Kanalmodell]] (<i>Binary Erasure Channel</i>) mit | Wir betrachten das so genannte [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| BEC–Kanalmodell]] (<i>Binary Erasure Channel</i>) mit | ||
| − | * der Eingangsgröße $x ∈ \{+1, \, | + | * der Eingangsgröße $x ∈ \{+1, \, -1\}$, |
| − | * der Ausgangsgröße $y ∈ \{+1, \, | + | * der Ausgangsgröße $y ∈ \{+1, \, -1, \, {\rm E}\}$, und |
* der Auslöschungswahrscheinlichket $\lambda$. | * der Auslöschungswahrscheinlichket $\lambda$. | ||
| − | Hierbei bedeutet $y = {\rm E}$ (<i>Erasure</i>), dass der Ausgangswert $y$ weder als „$+1$” noch als „$& | + | Hierbei bedeutet $y = {\rm E}$ (<i>Erasure</i>), dass der Ausgangswert $y$ weder als „$+1$” noch als „$&-1$” entschieden werden konnte. |
Bekannt sind zudem die Eingangswahrscheinlichkeiten | Bekannt sind zudem die Eingangswahrscheinlichkeiten | ||
:$${\rm Pr}(x = +1) = 3/4\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(x = -1) = 1/4\hspace{0.05cm}.$$ | :$${\rm Pr}(x = +1) = 3/4\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(x = -1) = 1/4\hspace{0.05cm}.$$ | ||
| − | Das | + | Das '''Log–Likelihood–Verhältnis''' (kurz: $L$–Wert, englisch: <i>Log Likelihood Ratio</i>, LLR) der binären Zufallsgröße $x$ ist bei bipolarer Betrachtungsweise wie folgt gegeben: |
:$$L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}\hspace{0.05cm}.$$ | :$$L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}\hspace{0.05cm}.$$ | ||
| − | Entsprechend gilt für den bedingten $L$–Wert in Vorwärtsrichtung für alle $y ∈ \{+1, \, | + | Entsprechend gilt für den bedingten $L$–Wert in Vorwärtsrichtung für alle $y ∈ \{+1, \, -1, \, {\rm E}\}$: |
:$$L(y\hspace{0.05cm}|\hspace{0.05cm}x) = | :$$L(y\hspace{0.05cm}|\hspace{0.05cm}x) = | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}. $$ | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}. $$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
* Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder| Soft–in Soft–out Decoder]]. | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder| Soft–in Soft–out Decoder]]. | ||
| + | * Bezug genommen wird insbesondere auf die Seite [[Kanalcodierung/Soft–in_Soft–out_Decoder#Zuverl.C3.A4ssigkeitsinformation_.E2.80.93_Log_Likelihood_Ratio| Zuverlässigkeitsinformation – Log Likelihood Ratio]] sowie auf die Seite [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Erasure_Channel_.E2.80.93_BEC|''Binary Erasure Channel'']]. | ||
* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | * Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 33: | Line 38: | ||
$L(x) \ = \ ${ 1.099 3% } | $L(x) \ = \ ${ 1.099 3% } | ||
| − | {Welcher Wahrscheinlichkeit ${\rm Pr}(x = \, | + | {Welcher Wahrscheinlichkeit ${\rm Pr}(x = \, -1)$ entspricht $L(x) = \, -2$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(x = \, | + | ${\rm Pr}(x = \, -1) \ = \ ${ 0.881 3% } |
{Berechnen Sie den bedingten $L$–Wert $L(y = {\rm E} | x)$ in Vorwärtsrichtung. | {Berechnen Sie den bedingten $L$–Wert $L(y = {\rm E} | x)$ in Vorwärtsrichtung. | ||
|type="{}"} | |type="{}"} | ||
| − | $L(y = {\rm E} | x) \ = \ ${ 0 | + | $L(y = {\rm E} | x) \ = \ ${ 0. } |
{Welche Aussagen gelten für die beiden anderen bedingten $L$–Wert? | {Welche Aussagen gelten für die beiden anderen bedingten $L$–Wert? | ||
|type="[]"} | |type="[]"} | ||
+ $L(y = +1 | x)$ ist positiv unendlich. | + $L(y = +1 | x)$ ist positiv unendlich. | ||
| − | + $L(y = \, | + | + $L(y = \, -1 | x)$ ist negativ und betragsmäßig unendlich groß. |
| − | - Es gilt $L(y = +1 | x) = L(y = \, | + | - Es gilt $L(y = +1 | x) = L(y = \, -1 | x) = 0$. |
{Unter welchen Voraussetzungen gelten die Ergebnisse aus (3) und (4)? | {Unter welchen Voraussetzungen gelten die Ergebnisse aus (3) und (4)? | ||
Revision as of 10:53, 29 January 2018
Wir betrachten das so genannte BEC–Kanalmodell (Binary Erasure Channel) mit
- der Eingangsgröße $x ∈ \{+1, \, -1\}$,
- der Ausgangsgröße $y ∈ \{+1, \, -1, \, {\rm E}\}$, und
- der Auslöschungswahrscheinlichket $\lambda$.
Hierbei bedeutet $y = {\rm E}$ (Erasure), dass der Ausgangswert $y$ weder als „$+1$” noch als „$&-1$” entschieden werden konnte.
Bekannt sind zudem die Eingangswahrscheinlichkeiten
- $${\rm Pr}(x = +1) = 3/4\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(x = -1) = 1/4\hspace{0.05cm}.$$
Das Log–Likelihood–Verhältnis (kurz: $L$–Wert, englisch: Log Likelihood Ratio, LLR) der binären Zufallsgröße $x$ ist bei bipolarer Betrachtungsweise wie folgt gegeben:
- $$L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}\hspace{0.05cm}.$$
Entsprechend gilt für den bedingten $L$–Wert in Vorwärtsrichtung für alle $y ∈ \{+1, \, -1, \, {\rm E}\}$:
- $$L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}. $$
Hinweise:
- Die Aufgabe gehört zum Kapitel Soft–in Soft–out Decoder.
- Bezug genommen wird insbesondere auf die Seite Zuverlässigkeitsinformation – Log Likelihood Ratio sowie auf die Seite Binary Erasure Channel.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)} ={\rm ln} \hspace{0.15cm} \frac{3/4}{1/4}\hspace{0.15cm}\underline{= 1.099}\hspace{0.05cm}.$$
(2) Entsprechend der Definition
- $$L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}$$
ergibt sich für $L(x) = \, –2$ die folgende Bestimmungsgleichung:
- $$\hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{1-{\rm Pr}(x = +1)} \stackrel{!}{=}{\rm e}^{-2} \approx 0.135 \hspace{0.25cm}\Rightarrow \hspace{0.25cm} 1.135 \cdot {\rm Pr}(x = +1)\stackrel{!}{=}0.135$$
- $$\Rightarrow \hspace{0.25cm} {\rm Pr}(x = +1) = 0.119\hspace{0.05cm},\hspace{0.4cm}{\rm Pr}(x = -1) \hspace{0.15cm}\underline{= 0.881}\hspace{0.05cm}. $$
(3) Für den bedingten $L$–Wert $L(y = {\rm E} | x)$ in Vorwärtsrichtung gilt beim vorgegebenen BEC–Modell:
- $$L(y = {\rm E}\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y= {\rm E}\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y= {\rm E}\hspace{0.05cm}|\hspace{0.05cm}x = -1)} = {\rm ln} \hspace{0.15cm} \frac{\lambda}{\lambda}\hspace{0.15cm}\underline{= 0}\hspace{0.05cm}.$$
(4) Analog zur Musterlösung der Teilaufgabe (3) erhält man für $y = ±1$:
- $$L(y = +1\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y= +1\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y= +1\hspace{0.05cm}|\hspace{0.05cm}x = -1)} = {\rm ln} \hspace{0.15cm} \frac{1-\lambda}{0}\hspace{0.15cm}\underline{ \hspace{0.05cm}\Rightarrow \hspace{0.15cm}+\infty }\hspace{0.05cm},$$
- $$L(y = -1\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y= -1\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y= -1\hspace{0.05cm}|\hspace{0.05cm}x = -1)} = {\rm ln} \hspace{0.15cm} \frac{0}{1-\lambda}\hspace{0.15cm}\underline{ \hspace{0.05cm}\Rightarrow \hspace{0.15cm}-\infty }\hspace{0.05cm}. $$
Richtig sind demnach die Lösungsvorschläge 1 und 2.
(5) Richtig ist der letzte Lösungsvorschlag:
- Für $\lambda = 0$ (idealer Kanal) ergibt sich $L(y = {\rm E} | x) = \ln {(0/0)}$ ⇒ unbestimmtes Ergebnis.
- Für $\lambda = 1$ (vollständige Auslöschung, $y ≡ {\rm E}$) sind $L(y = +1 | x)$ und $L(y = \, –1 | x)$ unbestimmt.