Difference between revisions of "Aufgaben:Exercise 4.1Z: Transmission Behavior of Short Cables"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige Ergebnisse der Leitungstheorie }} right| :Wir gehen von einer…“) |
|||
| Line 33: | Line 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Geben Sie <i>α</i>(<i>f</i>), <i>β</i>(<i>f</i>) und <i>Z</i><sub>W</sub>(<i>f</i>) für die Frequenz <i>f</i> = 0 (Gleichstrom) an. |
| − | |type=" | + | |type="{}"} |
| − | + | $f = 0:\ \alpha(f)$ = { 0.01 3% } $Np/km$ | |
| − | + | $\beta(f)$ = { 0 3% } $rad/km$ | |
| + | $Z_W(f)$ = { 10 3% } $k \omega$ | ||
| + | |||
| + | |||
| + | {Berechnen Sie das Dämpfungsmaß <i>α</i>(<i>f</i>) für <i>f</i> = 100 kHz. | ||
| + | |type="{}"} | ||
| + | $f = 100 kHz:\ \alpha(f)$ = { 0.486 3% } $Np/km$ | ||
| + | |||
| + | |||
| + | {Geben Sie für <i>f</i> → ∞ gültige Näherungen für <i>Z</i><sub>W</sub>(<i>f</i>) und <i>α</i>(<i>f</i>) an. | ||
| + | |type="{}"} | ||
| + | $f → ∞:\ Z_W(f) $ = { 100 3% } $\omega$ | ||
| + | $\alpha(f)$ = { 0.5 3% } $Np/km$ | ||
| + | |||
| + | |||
| + | {Leiten Sie mit <i>ωL</i>' << <i>R</i>', <i>G</i>' << <i>ωC</i>' eine Näherung für <i>α</i>(<i>f</i>) für (nicht zu) kleine Frequenzen ab. Welches Dämpfungsmaß ergibt sich für 1 kHz und 4 kHz. | ||
| + | |type="{}"} | ||
| + | $\alpha(f = 1\ kHz)$ = { 0.1 3% } $Np/km$ | ||
| + | $\alpha(f = 4\ kHz)$ = { 0.2 3% } $Np/km$ | ||
| − | { | + | {Geben Sie für den gleichen Frequenzbereich eine geeignete Näherung für den Wellenwiderstand <i>Z</i><sub>W</sub>(<i>f</i>) an. Welcher Wert ergibt sich für <i>f</i> = 1 kHz? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $Re\{Z_W(f = 1\ kHz)\}$ = { 500 3% } $\omega$ |
| + | $Im\{Z_W(f = 1\ kHz)\}$ = - { 500 3% } $\omega$ | ||
| Line 49: | Line 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | :<b>1.</b> Setzt man in die gegebenen Gleichungen die Frequenz <i>f</i> = 0 ein, so erhält man |
| − | '''2.''' | + | :$$\alpha(f = 0) = [1\,{\rm Np}] \cdot \sqrt{\frac {1}{2}\cdot R' \cdot G'+ \frac {1}{2}\cdot R' \cdot |
| − | '''3.''' | + | G'} = [1\,{\rm Np}] \cdot \sqrt{ R' \cdot G'} = \\ = [1\,{\rm Np}] \cdot \sqrt{ 100\,{\rm \Omega/km} \cdot 10^{-6}\,{\rm (\Omega \cdot km})^{-1}} |
| − | ''' | + | \hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} |
| − | '''5.''' | + | }\hspace{0.05cm},$$ |
| − | '''6.''' | + | :$$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{-\frac {1}{2}\cdot R' \cdot G'+ \frac {1}{2}\cdot R' \cdot |
| − | '''7.''' | + | G'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$ |
| + | :$$Z_{\rm W}(f = 0) = \sqrt{\frac {R'}{G'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm | ||
| + | k \Omega}}\hspace{0.05cm}.$$ | ||
| + | :Die Gleichsignaldämpfung wird relevant, wenn das Nutzsignal im Basisband übertragen werden soll und einen Gleichanteil besitzt, oder wenn der Netzabschluss beim Teilnehmer von der Ortsvermittlungsstelle aus mit Leistung versorgt werden muss (Fernspeisung). | ||
| + | |||
| + | :<b>2.</b> Mit <i>f</i> = 10<sup>5</sup> Hz und den angegebenen Werten gilt | ||
| + | :$$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | ||
| + | 10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm | ||
| + | \Omega | ||
| + | }{ {\rm km}} \hspace{0.05cm},\\ | ||
| + | f \cdot 2\pi C' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | ||
| + | 10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 | ||
| + | \,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$ | ||
| + | :Damit ergibt sich für das Dämpfungsmaß in Np/km: | ||
| + | :$$\frac{\alpha(f = 100\,{\rm kHz})}{\rm Np/km} =$$ | ||
| + | :$$ = \sqrt{\frac {1}{2}\cdot \left (100 \cdot 10^{-6} - 200 \cdot 0.02 \right)+ | ||
| + | \frac {1}{2}\sqrt{(100^2 + 200^2) \cdot (10^{-12} + 0.02^2)}} =\\ | ||
| + | \approx \sqrt{\frac {1}{2}\cdot \left (10^{-4} - 4 \right)+ | ||
| + | \frac {1}{2}\sqrt{5 \cdot 10^{4} \cdot 4 \cdot 10^{-4}}} \approx \sqrt {-2 + \frac{\sqrt{20}}{ | ||
| + | 2}} | ||
| + | \hspace{0.15cm}\underline{\approx 0.486} \hspace{0.05cm}.$$ | ||
| + | |||
| + | :<b>3.</b> Der Grenzübergang bezüglich des Wellenwiderstands für <i>f</i> → ∞ ergibt sich, wenn man im Zähler <i>R</i>' und im Nenner <i>G</i>' gegenüber den jeweils zweiten Term vernachlässigt: | ||
| + | :$$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) | ||
| + | = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C'}} | ||
| + | =\sqrt{\frac {2 \pi L' }{2 \pi C'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } | ||
| + | {2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$ | ||
| + | :Die Näherung für die Dämpfungsfunktion ist schwieriger herzuleiten. Ausgehend von | ||
| + | :$$\alpha(\omega) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ | ||
| + | \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} 2 \cdot \alpha^2(\omega) = R' G' + \omega^2 \cdot L' | ||
| + | C'\cdot | ||
| + | \left [-1 +\sqrt{(1 + \frac{R'^2}{ \omega^2 \cdot L'^2}) \cdot (1 + \frac{G'^2}{ \omega^2 \cdot C'^2})} \hspace{0.1cm} | ||
| + | \right]\approx \\ | ||
| + | \approx R' G' + \omega^2 \cdot L' | ||
| + | C'\cdot | ||
| + | \left [-1 +\sqrt{1 + \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G'^2}{ \omega^2 \cdot C'^2}} \hspace{0.1cm} | ||
| + | \right]$$ | ||
| + | :kommt man über die für kleine <i>x</i> gültige Näherung (1 + <i>x</i>)<sup>0.5</sup> ≈ 1 + <i>x</i>/2 zum Zwischenergebnis: | ||
| + | :$$2 \cdot \alpha^2(\omega \rightarrow \infty) = R' G' + \omega^2 \cdot L' | ||
| + | C'\cdot | ||
| + | \left [ -1 +1 + \frac{1}{2} \cdot \left ( \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G'^2}{ \omega^2 \cdot C'^2} | ||
| + | \right) \hspace{0.1cm} | ||
| + | \right] = \\ = \frac{2 \cdot R' G' C' L'+ R'\hspace{0.03cm}^2 C'\hspace{0.03cm}^2+ | ||
| + | G'\hspace{0.03cm}^2 L'\hspace{0.03cm}^2}{2 \cdot C' L' | ||
| + | }= | ||
| + | \frac{(R' C' + G' L')^2}{2 \cdot C' L' }$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = | ||
| + | \frac {1}{2}\cdot \frac{R' C' + G' L'}{\sqrt{ C' L' }}= | ||
| + | \frac {1}{2}\cdot \left [R' \cdot \sqrt{\frac{C'}{L'}}+G' \cdot \sqrt{\frac{L'}{C'}}\right]\hspace{0.05cm}.$$ | ||
| + | :Mit den eingesetzten Zahlenwerten ergibt sich | ||
| + | :$$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) | ||
| + | =\\ = | ||
| + | \frac {1\,{\rm Np/km}}{2}\cdot \left [100 \cdot \sqrt{\frac{2 \cdot 10^{-7}}{2 \cdot10^{-3}}}+10^{-6} \cdot | ||
| + | \sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] | ||
| + | \hspace{0.15cm}\underline{\approx 0.5 \, {\rm Np}/{\rm km}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | :<b>4.</b> Für kleine Frequenzen gilt <i>ωL</i>' << <i>R</i>' und <i>G</i>' << <i>ωC</i>'. Damit erhält man für das Dämpfungsmaß unter Vernachlässigung des <i>ω</i><sup>2</sup>–Anteils | ||
| + | :$$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ | ||
| + | \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} | ||
| + | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | ||
| + | f}\\ | ||
| + | \approx \sqrt{\frac {R' G'}{2}+ | ||
| + | \frac {R' \cdot \omega C'}{2}} | ||
| + | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | ||
| + | f} \approx \sqrt{ | ||
| + | \frac {1}{2} \cdot f \cdot R' \cdot 2 \pi C'} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | :Hierbei ist berücksichtigt, dass der erste Anteil außer bei der Frequenz <i>f</i> = 0 direkt (siehe Teilaufgabe a)) vernachlässigt werden kann. Für die Frequenz <i>f</i> = 1 kHz ergibt sich die Näherung | ||
| + | :$$\alpha(f = 1\,{\rm kHz}) = \sqrt{ | ||
| + | \frac {1}{2} \cdot 10^{3}\,{\rm Hz} \cdot 100\,\frac{\rm \Omega }{ {\rm km}} \cdot 2 \cdot 10^{-7} | ||
| + | \,\frac{\rm s }{ {\rm \Omega \cdot km}}} | ||
| + | \hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | :Für die Frequenz <i>f</i> = 4 kHz ist das Dämpfungsmaß doppelt so groß: | ||
| + | :$$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | :<b>5.</b> Für den Wellenwiderstand gilt bei niedrigen Frequenzen näherungsweise | ||
| + | :$$Z_{\rm W}(f) = \sqrt{\frac {R' + {\rm j} \cdot f \cdot 2 \pi L'}{G' + {\rm j} \cdot f \cdot 2 \pi C'}} | ||
| + | \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R' }{ f \cdot 2 \pi | ||
| + | C'}}= (1 - {\rm j})\cdot \sqrt{\frac {R' }{ 2 \cdot f \cdot 2 \pi | ||
| + | C'}}\hspace{0.05cm}.$$ | ||
| + | :Mit den angegebenen Leitungsbeschlägen erhält man | ||
| + | :$${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} | ||
| + | \,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm | ||
| + | \Omega}}\hspace{0.05cm},\\ | ||
| + | {\rm Im}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = -{\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\}\hspace{0.15cm}\underline{= -500\,{\rm | ||
| + | \Omega}}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 16:26, 1 October 2016
- Wir gehen von einer homogenen und reflektionsfrei abgeschlossenen Leitung der Länge l aus, so dass für die Spektralfunktion am Ausgang gilt:
- $$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
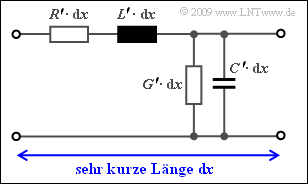
- Hierbei beschreibt γ(f) das Übertragungsmaß einer extrem kurzen Leitung der infinitesimalen Länge dx, das mit den Belägen R', L', G' und C' (siehe Grafik) wie folgt dargestellt werden kann:
- $$\gamma(f) = \sqrt{(R' + {\rm j} \cdot 2\pi f \cdot L') \cdot (G' + {\rm j} \cdot 2\pi f \cdot C')} = \alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$
- Der Realteil von γ(f) ergibt das Dämpfungsmaß α(f), der Imaginärteil das Phasenmaß β(f). Nach einiger Rechnung kann man für diese Größen schreiben:
- $$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f},$$
- $$\beta(f) = \sqrt{\frac {1}{2}\cdot \left (-R' G' + \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
- Beim Dämpfungsmaß ist zusätzlich die Pseudoeinheit „Neper (Np)” hinzuzufügen und beim Phasenmaß „Radian (rad)”. Da die Leitungsbeläge jeweils auf die Leitungslänge bezogen sind, weisen α(f) bzw. β(f) die Einheiten „Np/km” bzw. „rad/km” auf.
- Eine weitere wichtige Beschreibungsgröße neben γ(f) ist der Wellenwiderstand ZW(f), der an jedem Ort den Zusammenhang zwischen Spannung und Strom der beiden laufenden Wellen angibt. Es gilt:
- $$Z_{\rm W}(f) = \sqrt{\frac {R' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C'}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
- Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.1. Verwenden Sie für die numerischen Berechnungen jeweils die Zahlenwerte
- $$R\hspace{0.03cm}' = 100\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 1\,\,{\rm \mu S}/{ {\rm km}}\hspace{0.05cm},\hspace{0.3cm} 2\pi L' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} 2\pi C\hspace{0.03cm}' = 200\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- 1. Setzt man in die gegebenen Gleichungen die Frequenz f = 0 ein, so erhält man
- $$\alpha(f = 0) = [1\,{\rm Np}] \cdot \sqrt{\frac {1}{2}\cdot R' \cdot G'+ \frac {1}{2}\cdot R' \cdot G'} = [1\,{\rm Np}] \cdot \sqrt{ R' \cdot G'} = \\ = [1\,{\rm Np}] \cdot \sqrt{ 100\,{\rm \Omega/km} \cdot 10^{-6}\,{\rm (\Omega \cdot km})^{-1}} \hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} }\hspace{0.05cm},$$
- $$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{-\frac {1}{2}\cdot R' \cdot G'+ \frac {1}{2}\cdot R' \cdot G'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$
- $$Z_{\rm W}(f = 0) = \sqrt{\frac {R'}{G'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm k \Omega}}\hspace{0.05cm}.$$
- Die Gleichsignaldämpfung wird relevant, wenn das Nutzsignal im Basisband übertragen werden soll und einen Gleichanteil besitzt, oder wenn der Netzabschluss beim Teilnehmer von der Ortsvermittlungsstelle aus mit Leistung versorgt werden muss (Fernspeisung).
- 2. Mit f = 105 Hz und den angegebenen Werten gilt
- $$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot 10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm \Omega }{ {\rm km}} \hspace{0.05cm},\\ f \cdot 2\pi C' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot 10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 \,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$
- Damit ergibt sich für das Dämpfungsmaß in Np/km:
- $$\frac{\alpha(f = 100\,{\rm kHz})}{\rm Np/km} =$$
- $$ = \sqrt{\frac {1}{2}\cdot \left (100 \cdot 10^{-6} - 200 \cdot 0.02 \right)+ \frac {1}{2}\sqrt{(100^2 + 200^2) \cdot (10^{-12} + 0.02^2)}} =\\ \approx \sqrt{\frac {1}{2}\cdot \left (10^{-4} - 4 \right)+ \frac {1}{2}\sqrt{5 \cdot 10^{4} \cdot 4 \cdot 10^{-4}}} \approx \sqrt {-2 + \frac{\sqrt{20}}{ 2}} \hspace{0.15cm}\underline{\approx 0.486} \hspace{0.05cm}.$$
- 3. Der Grenzübergang bezüglich des Wellenwiderstands für f → ∞ ergibt sich, wenn man im Zähler R' und im Nenner G' gegenüber den jeweils zweiten Term vernachlässigt:
- $$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C'}} =\sqrt{\frac {2 \pi L' }{2 \pi C'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } {2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$
- Die Näherung für die Dämpfungsfunktion ist schwieriger herzuleiten. Ausgehend von
- $$\alpha(\omega) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}}$$
- $$\Rightarrow \hspace{0.3cm} 2 \cdot \alpha^2(\omega) = R' G' + \omega^2 \cdot L' C'\cdot \left [-1 +\sqrt{(1 + \frac{R'^2}{ \omega^2 \cdot L'^2}) \cdot (1 + \frac{G'^2}{ \omega^2 \cdot C'^2})} \hspace{0.1cm} \right]\approx \\ \approx R' G' + \omega^2 \cdot L' C'\cdot \left [-1 +\sqrt{1 + \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G'^2}{ \omega^2 \cdot C'^2}} \hspace{0.1cm} \right]$$
- kommt man über die für kleine x gültige Näherung (1 + x)0.5 ≈ 1 + x/2 zum Zwischenergebnis:
- $$2 \cdot \alpha^2(\omega \rightarrow \infty) = R' G' + \omega^2 \cdot L' C'\cdot \left [ -1 +1 + \frac{1}{2} \cdot \left ( \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G'^2}{ \omega^2 \cdot C'^2} \right) \hspace{0.1cm} \right] = \\ = \frac{2 \cdot R' G' C' L'+ R'\hspace{0.03cm}^2 C'\hspace{0.03cm}^2+ G'\hspace{0.03cm}^2 L'\hspace{0.03cm}^2}{2 \cdot C' L' }= \frac{(R' C' + G' L')^2}{2 \cdot C' L' }$$
- $$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = \frac {1}{2}\cdot \frac{R' C' + G' L'}{\sqrt{ C' L' }}= \frac {1}{2}\cdot \left [R' \cdot \sqrt{\frac{C'}{L'}}+G' \cdot \sqrt{\frac{L'}{C'}}\right]\hspace{0.05cm}.$$
- Mit den eingesetzten Zahlenwerten ergibt sich
- $$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) =\\ = \frac {1\,{\rm Np/km}}{2}\cdot \left [100 \cdot \sqrt{\frac{2 \cdot 10^{-7}}{2 \cdot10^{-3}}}+10^{-6} \cdot \sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] \hspace{0.15cm}\underline{\approx 0.5 \, {\rm Np}/{\rm km}}\hspace{0.05cm}.$$
- 4. Für kleine Frequenzen gilt ωL' << R' und G' << ωC'. Damit erhält man für das Dämpfungsmaß unter Vernachlässigung des ω2–Anteils
- $$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\\ \approx \sqrt{\frac {R' G'}{2}+ \frac {R' \cdot \omega C'}{2}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f} \approx \sqrt{ \frac {1}{2} \cdot f \cdot R' \cdot 2 \pi C'} \hspace{0.05cm}.$$
- Hierbei ist berücksichtigt, dass der erste Anteil außer bei der Frequenz f = 0 direkt (siehe Teilaufgabe a)) vernachlässigt werden kann. Für die Frequenz f = 1 kHz ergibt sich die Näherung
- $$\alpha(f = 1\,{\rm kHz}) = \sqrt{ \frac {1}{2} \cdot 10^{3}\,{\rm Hz} \cdot 100\,\frac{\rm \Omega }{ {\rm km}} \cdot 2 \cdot 10^{-7} \,\frac{\rm s }{ {\rm \Omega \cdot km}}} \hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} \hspace{0.05cm}.$$
- Für die Frequenz f = 4 kHz ist das Dämpfungsmaß doppelt so groß:
- $$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} \hspace{0.05cm}.$$
- 5. Für den Wellenwiderstand gilt bei niedrigen Frequenzen näherungsweise
- $$Z_{\rm W}(f) = \sqrt{\frac {R' + {\rm j} \cdot f \cdot 2 \pi L'}{G' + {\rm j} \cdot f \cdot 2 \pi C'}} \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R' }{ f \cdot 2 \pi C'}}= (1 - {\rm j})\cdot \sqrt{\frac {R' }{ 2 \cdot f \cdot 2 \pi C'}}\hspace{0.05cm}.$$
- Mit den angegebenen Leitungsbeschlägen erhält man
- $${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} \,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm \Omega}}\hspace{0.05cm},\\ {\rm Im}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = -{\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\}\hspace{0.15cm}\underline{= -500\,{\rm \Omega}}\hspace{0.05cm}.$$