Difference between revisions of "Aufgaben:Exercise 4.2: UMTS Radio Channel Basics"
From LNTwww
m (Guenter verschob die Seite 4.2 UMTS-Funkkanal nach Aufgabe 4.2: UMTS-Funkkanal) |
|||
| (21 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/General_Description_of_UMTS |
}} | }} | ||
| − | [[File: | + | [[File:EN_Bei_A_4_2_v2.png|right|frame|Path loss, frequency/time–selective fading ]] |
| − | + | UMTS also has quite a few effects leading to degradation that must be taken into account during system planning: | |
| − | *$ | + | *${\rm Interference}$: Since all users are simultaneously served in the same frequency band, each user is interfered by other users. |
| − | |||
| − | |||
| − | |||
| − | + | *${\rm Path\:loss}$: The received power $P_{\rm E}$ of a radio signal decreases with distance $d$ by a factor $d^{- \gamma}$. | |
| − | + | ||
| − | + | *${\rm Multipath\:propagation}$: The signal reaches the mobile receiver not only through the direct path, but through several paths – differently attenuated and differently delayed. | |
| + | |||
| + | *${\rm Doppler\:effect}$: If transmitter and/or receiver move, frequency shifts can occur depending on speed and the direction $($Which angle? Towards each other? Away from each other?$)$. | ||
| + | |||
| + | |||
| + | In the book "[[Mobile Communications]]" these effects have already been discussed in detail. The diagrams convey only a few pieces of information regarding | ||
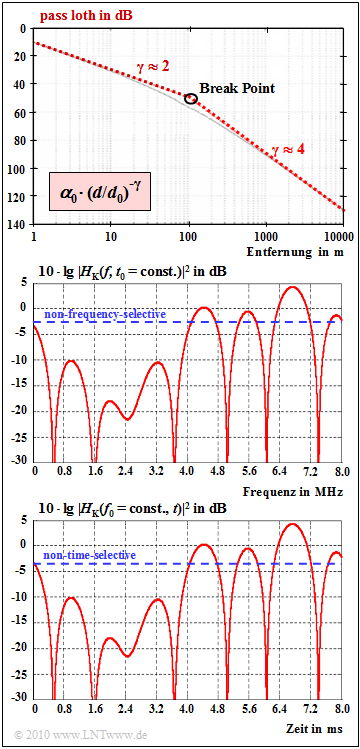
| + | *<u>Path loss:</u> Path loss indicates the decrease in the received power with distance $d$ from the transmitter. Above the so-called "break point" applies approximately to the received power: | ||
| + | ::$$\frac{P(d)}{P(d_0)} = \alpha_0 \cdot \left ( {d}/{d_0}\right )^{-4}.$$ | ||
| + | :According to the upper graph $\alpha_{0} = 10^{-5}$ $($correspondingly $50 \ \rm dB)$ and $d_{0} = 100 \ \rm m$. | ||
| + | |||
| + | *<u>Frequency-selective fading:</u> The power transfer function $|H_{\rm K}(f)|^{2}$ at a given time according to the middle graph illustrates frequency-selective fading. The blue-dashed horizontal line, on the other hand, indicates non-frequency-selective fading. | ||
| + | ::Such frequency-selective fading occurs when the coherence bandwidth $B_{\rm K}$ is much smaller than the signal bandwidth $B_{\rm S}$. Here, with the "delay spread" $T_{\rm V}$ ⇒ difference between the maximum and minimum delay times: | ||
| + | ::$$B_{\rm K}\approx \frac{1}{T_{\rm V}}= \frac{1}{\tau_{\rm max}- \tau_{\rm min}}.$$ | ||
| − | + | *<u>Time-selective fading:</u> The bottom graph shows the power transfer function $|H_{\rm K}(t)|^{2}$ for a fixed frequency $f_{0}$. The sketch is to be understood schematically, because for the time-selective fading considered here exactly the same course was chosen as in the middle diagram for the frequency-selective fading $($pure convenience of the author$)$. | |
| + | ::Here a so-called "Doppler spread" $B_{\rm D}$ arises, defined as the difference between the maximum and the minimum Doppler frequency. The inverse $T_{\rm D} = 1/B_{\rm D}$ is called "coherence time" or also "correlation duration". In UMTS, time-selective fading occurs whenever $T_{\rm D} \ll T_{\rm C}$ $($chip duration$)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <u>Hints:</u> | |
| − | |||
| − | |||
| − | + | *This exercise belongs to the chapter [[Examples_of_Communication_Systems/General_Description_of_UMTS|"General Description of UMTS"]]. | |
| − | + | ||
| − | + | *Reference is made in particular to the sections [[Examples_of_Communication_Systems/General_Description_of_UMTS#Properties_of_the_UMTS_radio_channel|"Properties of the UMTS radio channel"]] and [[Examples_of_Communication_Systems/General_Description_of_UMTS#Frequency.E2.80.93selective_and_time.E2.80.93selective_fading|"Frequency-selective and time-selective fading"]]. | |
| − | |||
| + | *For UMTS, the bandwidth: $B_{\rm S} = 5 \ \rm MHz$ and the chip duration: $T_{\rm C} \approx 0.26 \ \rm µ s$. | ||
| + | |||
| − | |||
| − | + | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Starting from the top graph on the information page, calculate the path loss $($in $\rm dB)$ for $d = \rm 5 \ km$. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm | + | ${\rm path\ loss} \ = \ $ { 118 3% } $\ \rm dB $. |
| − | { | + | {What statements are true regarding frequency-selective fading? |
|type="[]"} | |type="[]"} | ||
| − | + | + This is caused by multipath reception. | |
| − | + | - It is caused by movement of transmitter and/or receiver. | |
| − | + | + | + Different frequencies are attenuated differently. |
| − | + | + | + An echo at a distance $1\ \rm µ s$ results in frequency-selective fading. |
| − | { | + | {What statements are true regarding time-selective fading? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - This arises due to multipath reception. |
| − | + | + | + It results from movement of transmitter and/or receiver. |
| − | - | + | - Different frequencies are attenuated differently. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' According to the sketch, the breakpoint is at $d_{0} = 100 \ \rm m$. |
| − | :$${\rm | + | *For $d ≤ d_{0}$, the path loss is equal to $\alpha_{0} \cdot (d/d_{0})^{-2}$. For $d = d_{0} = 100 \ \rm m$ holds: |
| − | + | :$${\rm path\ loss} = \alpha_0 = 10^{-5}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{50\,{\rm dB}}.$$ | |
| − | :$${\rm | + | |
| + | *Above $d_{0}$, the path loss is equal to $\alpha_{0} \cdot (d/d_{0})^{-4}$. Thus, at $5 \ \rm km$ distance, one obtains: | ||
| + | :$${\rm path\ loss} = 10^{-5}\cdot 50^{-4} = 1.6 \cdot 10^{-12}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\underline{118\,{\rm dB}}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Correct are the <u>statements 1, 3, and 4</u>: | ||
| + | *Frequency-selective fading is due to multipath reception. This means: | ||
| + | |||
| + | *Different frequency components are delayed and attenuated differently by the channel. | ||
| + | |||
| + | *This results in attenuation and phase distortion. | ||
| + | |||
| + | *Because $\tau_{\rm max} = 1 \ \rm µ s$ $($simplifying $\tau_{\rm min} = 0$ is set$)$ further results in | ||
| + | :$$B_{\rm K} = \frac{1}{\tau_{\rm max}- \tau_{\rm min}} = 1\,{\rm MHz}\ \ll \ B_{\rm S} \hspace{0.15cm}\underline {= 5\,{\rm MHz}}.$$ | ||
| − | |||
| − | |||
| − | '''(3)''' | + | '''(3)''' Correct is <u>statement 2</u>. |
| + | *Statements 1 and 3, on the other hand, are valid for frequency-selective fading – see subtask '''(2)'''. | ||
| Line 77: | Line 93: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^4.1 General Description of UMTS |
^]] | ^]] | ||
Latest revision as of 17:26, 13 February 2023
UMTS also has quite a few effects leading to degradation that must be taken into account during system planning:
- ${\rm Interference}$: Since all users are simultaneously served in the same frequency band, each user is interfered by other users.
- ${\rm Path\:loss}$: The received power $P_{\rm E}$ of a radio signal decreases with distance $d$ by a factor $d^{- \gamma}$.
- ${\rm Multipath\:propagation}$: The signal reaches the mobile receiver not only through the direct path, but through several paths – differently attenuated and differently delayed.
- ${\rm Doppler\:effect}$: If transmitter and/or receiver move, frequency shifts can occur depending on speed and the direction $($Which angle? Towards each other? Away from each other?$)$.
In the book "Mobile Communications" these effects have already been discussed in detail. The diagrams convey only a few pieces of information regarding
- Path loss: Path loss indicates the decrease in the received power with distance $d$ from the transmitter. Above the so-called "break point" applies approximately to the received power:
- $$\frac{P(d)}{P(d_0)} = \alpha_0 \cdot \left ( {d}/{d_0}\right )^{-4}.$$
- According to the upper graph $\alpha_{0} = 10^{-5}$ $($correspondingly $50 \ \rm dB)$ and $d_{0} = 100 \ \rm m$.
- Frequency-selective fading: The power transfer function $|H_{\rm K}(f)|^{2}$ at a given time according to the middle graph illustrates frequency-selective fading. The blue-dashed horizontal line, on the other hand, indicates non-frequency-selective fading.
- Such frequency-selective fading occurs when the coherence bandwidth $B_{\rm K}$ is much smaller than the signal bandwidth $B_{\rm S}$. Here, with the "delay spread" $T_{\rm V}$ ⇒ difference between the maximum and minimum delay times:
- $$B_{\rm K}\approx \frac{1}{T_{\rm V}}= \frac{1}{\tau_{\rm max}- \tau_{\rm min}}.$$
- Time-selective fading: The bottom graph shows the power transfer function $|H_{\rm K}(t)|^{2}$ for a fixed frequency $f_{0}$. The sketch is to be understood schematically, because for the time-selective fading considered here exactly the same course was chosen as in the middle diagram for the frequency-selective fading $($pure convenience of the author$)$.
- Here a so-called "Doppler spread" $B_{\rm D}$ arises, defined as the difference between the maximum and the minimum Doppler frequency. The inverse $T_{\rm D} = 1/B_{\rm D}$ is called "coherence time" or also "correlation duration". In UMTS, time-selective fading occurs whenever $T_{\rm D} \ll T_{\rm C}$ $($chip duration$)$.
Hints:
- This exercise belongs to the chapter "General Description of UMTS".
- Reference is made in particular to the sections "Properties of the UMTS radio channel" and "Frequency-selective and time-selective fading".
- For UMTS, the bandwidth: $B_{\rm S} = 5 \ \rm MHz$ and the chip duration: $T_{\rm C} \approx 0.26 \ \rm µ s$.
Questions
Solution
(1) According to the sketch, the breakpoint is at $d_{0} = 100 \ \rm m$.
- For $d ≤ d_{0}$, the path loss is equal to $\alpha_{0} \cdot (d/d_{0})^{-2}$. For $d = d_{0} = 100 \ \rm m$ holds:
- $${\rm path\ loss} = \alpha_0 = 10^{-5}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{50\,{\rm dB}}.$$
- Above $d_{0}$, the path loss is equal to $\alpha_{0} \cdot (d/d_{0})^{-4}$. Thus, at $5 \ \rm km$ distance, one obtains:
- $${\rm path\ loss} = 10^{-5}\cdot 50^{-4} = 1.6 \cdot 10^{-12}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\underline{118\,{\rm dB}}.$$
(2) Correct are the statements 1, 3, and 4:
- Frequency-selective fading is due to multipath reception. This means:
- Different frequency components are delayed and attenuated differently by the channel.
- This results in attenuation and phase distortion.
- Because $\tau_{\rm max} = 1 \ \rm µ s$ $($simplifying $\tau_{\rm min} = 0$ is set$)$ further results in
- $$B_{\rm K} = \frac{1}{\tau_{\rm max}- \tau_{\rm min}} = 1\,{\rm MHz}\ \ll \ B_{\rm S} \hspace{0.15cm}\underline {= 5\,{\rm MHz}}.$$
(3) Correct is statement 2.
- Statements 1 and 3, on the other hand, are valid for frequency-selective fading – see subtask (2).