Exercise 4.2Z: Mixed Random Variables

PDF of $X$ (top), and
CDF of $Y$ (bottom)

One speaks of a "mixed random variable", if the random variable contains discrete components in addition to a continuous component.

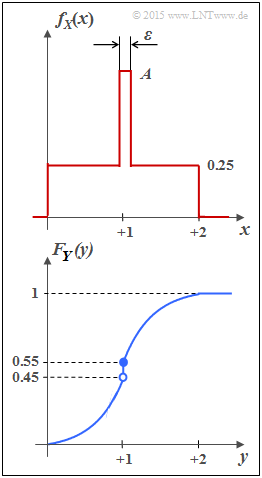
For example, the random variable $Y$ with cumulative distribution function $F_Y(y)$ as shown in the sketch below has both a continuous and a discrete component.
The probability density function $f_Y(y)$ is obtained from $F_Y(y)$ by differentiation.
The jump at $y= 1$ in the CDF thus becomes a "Dirac" in the probability density function.

In subtask (4) the differential entropy $h(Y)$ of the random variable $Y$ is to be determined (in bit), assuming the following equation:

$$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$

In subtask (2) , calculate the differential entropy $h(X)$ of the random variable $X$ whose PDF $f_X(x)$ is sketched above. If one performs a suitable boundary transition, the random variable $X$ also becomes a mixed random variable.

Hints:

The exercise belongs to the chapter Differential Entropy.
Further information on mixed random variables can be found in the chapter Cumulative Distribution Function of the book "Theory of Stochastic Signals".

Fragebogen

Musterlösung

Solution

(1) Richtig ist der Lösungsvorschlag 2, weil das Integral über die WDF $1$ ergeben muss:

$$f_X(x) \hspace{0.1cm}{\rm d}x = 0.25 \cdot 2 + (A - 0.25) \cdot \varepsilon \stackrel{!}{=} 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}(A - 0.25) \cdot \varepsilon \stackrel{!}{=} 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.5/\varepsilon +0.25\hspace{0.05cm}.$$

(2) Die differentielle Entropie (in "bit") ist wie folgt gegeben:

$$h(X) = \hspace{0.1cm} \hspace{-0.45cm} \int\limits_{{\rm supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{f_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Wir unterteilen nun das Integral in drei Teilintegrale:

$$h(X) = \hspace{-0.25cm} \int\limits_{0}^{1-\varepsilon/2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1+\varepsilon/2}^{2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1-\varepsilon/2}^{1+\varepsilon/2} \hspace{-0.15cm} \big [0.5/\varepsilon + 0.25 \big ] \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5/\varepsilon + 0.25} \hspace{0.1cm}{\rm d}x $$

$$ \Rightarrow \hspace{0.3cm} h(X) = 2 \cdot 0.25 \cdot 2 \cdot (2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25) \hspace{0.05cm}.$$

Insbesondere erhält man

für $\varepsilon = 0.1$:

$$h(X) =1.9 - 0.525 \cdot {\rm log}_2 \hspace{0.1cm}(5.25) = 1.9 - 1.256 \hspace{0.15cm}\underline{= 0.644\,{\rm bit}} \hspace{0.05cm},$$

für $\varepsilon = 0.01$:

$$h(X) =1.99 - 0.5025 \cdot {\rm log}_2 \hspace{0.1cm}(50.25)= 1.99 - 2.84 \hspace{0.15cm}\underline{= -0.850\,{\rm bit}} \hspace{0.05cm}$$

für $\varepsilon = 0.001$:

$$h(X) =1.999 - 0.50025 \cdot {\rm log}_2 \hspace{0.1cm}(500.25) = 1.999 - 8.967 \hspace{0.15cm}\underline{= -6.968\,{\rm bit}} \hspace{0.05cm}.$$

(3) Alle Lösungsvorschläge sind zutreffend:

Nach dem Grenzübergang $\varepsilon → 0$ erhält man für die differentielle Entropie

$$h(X) = \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0} \hspace{0.1cm}\big[(2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25)\big] = 2\,{\rm bit} - 0.5 \cdot \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}{\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} - \infty \hspace{0.05cm}.$$

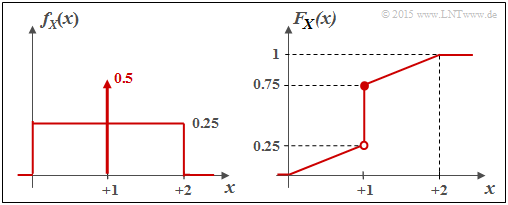
WDF und VTF der gemischten Zufallsgröße $X$

Die Wahrscheinlichkeitsdichtefunktion (WDF) ergibt sich in diesem Fall zu

$$f_X(x) = \left\{ \begin{array}{c} 0.25 + 0.5 \cdot \delta (x-1) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 2, \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.$$

Es handelt sich demzufolge um eine "gemischte" Zufallsgröße mit

einem stochastischen, gleichverteilten Anteil im Bereich $0 \le x \le 2$, und
einem diskreten Anteil bei $x = 1$ mit der Wahrscheinlichkeit $0.5$.

Die Grafik zeigt links die WDF $f_X(x)$ und rechts die Verteilungsfunktion $F_X(x)$.
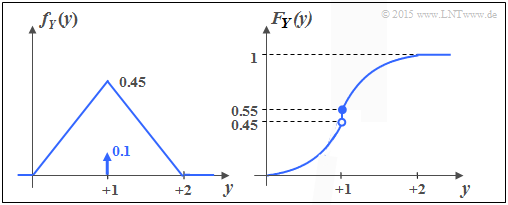
(4) Richtig sind die Lösungsvorschläge 2, 3 und 5. Die untere Grafik zeigt die WDF und die VTF der Zufallsgröße $Y$. Man erkennt:

WDF und VTF der gemischten Zufallsgröße $Y$

$Y$ beinhaltet wie $X$ einen kontinuierlichen und einen diskreten Anteil.
Der diskrete Anteil tritt mit der Wahrscheinlichkeit ${\rm Pr}(Y = 1) = 0.1$ auf.
Da $F_Y(y)= {\rm Pr}(Y \le y)$ gilt, ergibt sich der rechtsseitige Grenzwert:

$$F_Y(y = 1) = 0.55.$$

Der kontinuierliche Anteil ist nicht gleichverteilt; vielmehr liegt eine Dreieckverteilung vor.
Richtig ist auch der letzte Vorschlag: $h(Y) = h(X) = - \infty$.

Denn: Bei jeder Zufallsgröße mit einem diskreten Anteil – und ist er auch noch so klein, ist die differentielle Entropie gleich minus unendlich.

	Der VTF–Wert an der Stelle $y = 1$ ist $0.5$.
	$Y$ beinhaltet einen diskreten und einen kontinuierlichen Anteil.
	Der diskrete Anteil bei $Y = 1$ tritt mit $10\%$ Wahrscheinlichkeit auf.
	Der kontinuierliche Anteil von $Y$ ist gleichverteilt.
	Die differentiellen Entropien von $X$ und $Y$ sind gleich.

	$A = 0.5/\varepsilon$,
	$A = 0.5/\varepsilon+0.25$,
	$A = 1/\varepsilon$.

	$f_X(x)$ hat nun einen kontinuierlichen und einen diskreten Anteil.
	Die differentielle Energie $h(X)$ ist negativ.
	Der Betrag $\|h(X)\|$ ist unendlich groß.