Difference between revisions of "Aufgaben:Exercise 4.3Z: Conversions of L-value and S-value"
m (Guenter moved page Aufgabe 4.3Z: Umrechnungen von L–Wert und S–Wert to Exercise 4.3Z: Conversions of L-value and S-value) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} |
| − | [[File:P_ID3093__KC_Z_4_3neu_v1.png|right|right|frame| | + | [[File:P_ID3093__KC_Z_4_3neu_v1.png|right|right|frame|Function $y = \tanh {(x)}$ <br>in tabular form.]] |
| − | + | We assume a binary random variable $x ∈ \{+1, \, -1\}$ with the following probabilities: | |
:$${\rm Pr}(x =+1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} p\hspace{0.05cm},$$ | :$${\rm Pr}(x =+1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} p\hspace{0.05cm},$$ | ||
:$${\rm Pr}(x =-1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} q = 1-p\hspace{0.05cm}.$$ | :$${\rm Pr}(x =-1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} q = 1-p\hspace{0.05cm}.$$ | ||
| − | + | The "reliability" of the symbol $x$ can be expressed | |
| − | * | + | * by the $L$ value (LLR) according to the definition |
:$$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} | :$$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | * by the so called $S$ value. |
:$$S(x) = p- q \hspace{0.05cm}.$$ | :$$S(x) = p- q \hspace{0.05cm}.$$ | ||
| − | + | We have created the term "$S$ value" in order to be able to formulate the following questions more succinctly. In the literature, one sometimes finds the term "soft bit" for this. | |
| − | + | As will be shown in subtask '''(1)''', $L(x)$ and $S(x)$ can be converted into each other. | |
| − | + | Subsequently, these functions shall be used to calculate the following quantities, always assuming code length $n = 3$ : | |
| − | * | + | * the extrinsic $L$–value for the third symbol ⇒ $L_{\rm E}(x_3)$, |
| − | * | + | * the a posteriori–$L$–value for the third symbol ⇒ $L_{\rm APP}(x_3)$. |
| − | + | The calculation should be done for the following codes: | |
| − | * | + | * the repetition Code [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes|$\text{"RC (3, 1, 3)"}$]] with the constraint $\sign {(x_1)} = \sign {(x_2)} = \sign {(x_3)}$, |
| − | * | + | * the single parity–code ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes|$\text{"SPC (3, 2, 2)"}$]] with the constraint $x_1 \cdot x_2 \cdot x_3 = +1$. |
| Line 32: | Line 32: | ||
| − | + | Hints: | |
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder| "Soft–in Soft–out Decoder"]]. |
| − | * | + | * Reference is made in particular to the page [[Channel_Coding/Soft-in_Soft-Out_Decoder#Reliability_information_-_Log_Likelihood_Ratio| "Reliability Information – Log Likelihood Ratio"]]. |
| − | * | + | * To solve, you need the <i>hyperbolic tangent</i> according to the following definition (this function is given above in tabular form): |
:$$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} | :$$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} | ||
= \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} | = \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} | ||
| Line 42: | Line 42: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the relationship between $S$ value and $L$ value? |
|type="[]"} | |type="[]"} | ||
- $S(x) = \tanh {(L(x))}$, | - $S(x) = \tanh {(L(x))}$, | ||
| Line 50: | Line 50: | ||
+ $L(x) = 2 \cdot \tanh^{-1}{(S(x))}$. | + $L(x) = 2 \cdot \tanh^{-1}{(S(x))}$. | ||
| − | { | + | {The $\text{RC (3, 1, 3)}$ is considered. For the apriori $L$ values, let $\underline{L}_{\rm A} = (+2, -1, +3)$. What is the extrinsic $L$ value for the symbol $x_3$? |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ 1 3% } | $L_{\rm E}(x_3) \ = \ ${ 1 3% } | ||
| − | { | + | {What is the aposteriori $L$ value for the symbol $x_3$ in this case? |
|type="{}"} | |type="{}"} | ||
$L_{\rm APP}(x_3) \ = \ ${ 4 3% } | $L_{\rm APP}(x_3) \ = \ ${ 4 3% } | ||
| − | { | + | {What is the extrinsic $L$ value at $\text{SPC (3, 2, 2)}$? It is still valid $\underline{L}_{\rm A} = (+2, -1, +3)$. |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ -0.757256--0.713144 } | $L_{\rm E}(x_3) \ = \ ${ -0.757256--0.713144 } | ||
| − | { | + | {The apriori probabilities are now $0.3, \ 0.8$ and $0.9$. What is the extrinsic $L$ value for the <i>repetition code</i>? |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ 0.535 3% } | $L_{\rm E}(x_3) \ = \ ${ 0.535 3% } | ||
| − | { | + | {What extrinsic $L$ value results for the <i>single parity–check code</i> given the same conditions as in ''(5)'''' ? |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ 0.49 3% } | $L_{\rm E}(x_3) \ = \ ${ 0.49 3% } | ||
Revision as of 19:55, 27 October 2022
We assume a binary random variable $x ∈ \{+1, \, -1\}$ with the following probabilities:
- $${\rm Pr}(x =+1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} p\hspace{0.05cm},$$
- $${\rm Pr}(x =-1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} q = 1-p\hspace{0.05cm}.$$
The "reliability" of the symbol $x$ can be expressed
- by the $L$ value (LLR) according to the definition
- $$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} \hspace{0.05cm},$$
- by the so called $S$ value.
- $$S(x) = p- q \hspace{0.05cm}.$$
We have created the term "$S$ value" in order to be able to formulate the following questions more succinctly. In the literature, one sometimes finds the term "soft bit" for this.
As will be shown in subtask (1), $L(x)$ and $S(x)$ can be converted into each other.
Subsequently, these functions shall be used to calculate the following quantities, always assuming code length $n = 3$ :
- the extrinsic $L$–value for the third symbol ⇒ $L_{\rm E}(x_3)$,
- the a posteriori–$L$–value for the third symbol ⇒ $L_{\rm APP}(x_3)$.
The calculation should be done for the following codes:
- the repetition Code $\text{"RC (3, 1, 3)"}$ with the constraint $\sign {(x_1)} = \sign {(x_2)} = \sign {(x_3)}$,
- the single parity–code ⇒ $\text{"SPC (3, 2, 2)"}$ with the constraint $x_1 \cdot x_2 \cdot x_3 = +1$.
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the page "Reliability Information – Log Likelihood Ratio".
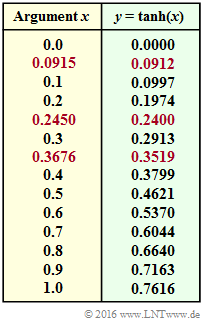
- To solve, you need the hyperbolic tangent according to the following definition (this function is given above in tabular form):
- $$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} = \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} \hspace{0.05cm}.$$
Questions
Musterlösung
- $p = {\rm Pr}(x = +1)$, und
- $p = {\rm Pr}(x=-1) = 1-p$
gelten folgende Definitionen:
- $$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} -\infty \le L(x) \le +\infty \hspace{0.05cm},$$
- $$S(x) = p- q = 2 \cdot p - 1\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} -1 \le S(x) \le +1 \hspace{0.05cm}.$$
- Ausgehend vom $S$–Wert erhält man wegen $p + q = 1$:
- $$S(x) = p- q = \frac{p- q}{p+ q} = \frac{1- q/p}{1+ q/p} \hspace{0.05cm}.$$
- Gleichzeitig gilt $q/p = {\rm e}^{-L(x)}$. Daraus folgt:
- $$S(x) = \frac{1- {\rm e}^{-L(x)}}{1+ {\rm e}^{-L(x)}} \hspace{0.05cm}.$$
- Multipliziert man Zähler und Nenner mit ${\rm e}^{-L(x)/2}$, so erhält man schließlich:
- $$S(x) = \frac{{\rm e}^{+L(x)/2}- {\rm e}^{-L(x)/2}}{{\rm e}^{+L(x)/2}+ {\rm e}^{-L(x)/2}} = {\rm tanh}\big [L(x)/2. \big] \hspace{0.05cm}.$$
- Die Umkehrfunktion ergibt
- $$L(x) = 2 \cdot {\rm tanh}^{-1}[S(x)] \hspace{0.05cm}.$$
Richtig sind somit die Lösungsvorschläge 2 und 3. Die Tabelle zeigt den $L$–Wert $S$–Wert für einige Wahrscheinlichkeiten $p = {\rm Pr}(x=+1)$.
(2) Der extrinsische $L$–Wert für das Symbol $x_3$ berücksichtigt nur die Apriori–$L$–Werte $L_{\rm A}(x_1)$ und $L_{\rm A}(x_2)$, nicht jedoch $L_{\rm A}(x_3)$.
- Beim (3, 1) Repetition Code ergibt sich hierfür:
- $$L_{\rm E}(x_3) = L_{\rm A}(x_1) + L_{\rm A}(x_2) = 2 + (-1) \hspace{0.15cm} \underline{= +1}\hspace{0.05cm}.$$
(3) Für den Aposteriori–$L$–Wert erhält man somit:
- $$L_{\rm APP}(x_3) = L_{\rm A}(x_3) + L_{\rm E}(x_3) = 3 + 1 \hspace{0.15cm} \underline{= +4}\hspace{0.05cm}.$$
(4) Beim Single Parity–check Code lautet die entsprechende Berechnungsvorschrift:
- $$L_{\rm E}(x_3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh}(x_1/2) \cdot {\rm tanh}(x_2/2) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh}(+1) \cdot {\rm tanh}(-0.5) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ 0.7616 \cdot (-0.4621) \right ] $$
- $$\Rightarrow \hspace{0.3cm}L_{\rm E}(x_3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ -0.3519 \right ] =-2 \cdot 0.3676\hspace{0.15cm} \underline{= -0.7352}\hspace{0.05cm}.$$
Das Ergebnis ${\rm tanh}^{-1} (-0.3519) = 0.3676$ wurde der Tabelle auf der Angabenseite entnommen.
(5) Beim Wiederholungscode der Länge $n = 3$ gilt wie in der Teilaufgabe (3):
- $$L_{\rm E}(x_3) = L_{\rm A}(x_1) + L_{\rm A}(x_2) = -0.847 +1.382 \hspace{0.15cm} \underline{= +0.535}\hspace{0.05cm}.$$
Benutzt wurden hierbei die $L$–Werte entsprechend der Tabelle zur Teilaufgabe (1), zum Beispiel ${\rm Pr}(x_1 = +1) = 0.3$ ⇒ $L_{\rm A}(x_1) = -0.847$.
(6) Nachdem hier anstelle der Apriori–$L$–Werte die Apriori–Wahrscheinlichkeiten gegeben sind, kommt man gegenüber der Teilaufgabe (4) auf dem Umweg über den extrinsischen $S$–Wert schneller zum Erfolg.
- Die extrinsische Wahrscheinlichkeit für das dritte Symbol bezeichnen wir hier mit $P_{\rm E}(x_3)$. Für diese gilt:
- $$P_{\rm E}(x_3 = +1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} P_{\rm A}(x_1 = +1) \cdot P_{\rm A}(x_2 = -1) + P_{\rm A}(x_1 = -1) \cdot P_{\rm A}(x_2 = +1) = 0.3 \cdot (1-0.8) + (1-0.3) \cdot 0.8 = 0.62\hspace{0.05cm}.$$
- Daraus ergeben sich für die weiteren Größen:
- $$S_{\rm E}(x_3) = P_{\rm E}(x_3 = +1) - P_{\rm E}(x_3 = - 1) = 0.62 -0.38 = 0.24\hspace{0.05cm},$$
- $$L_{\rm E}(x_3) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ S_{\rm E}(x_3) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} (0.24) = 2 \cdot 0.245 \hspace{0.15cm} \underline{= +0.49}\hspace{0.05cm}$$