Difference between revisions of "Aufgaben:Exercise 4.3Z: Conversions of L-value and S-value"
| Line 2: | Line 2: | ||
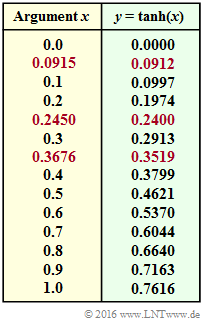
[[File:P_ID3093__KC_Z_4_3neu_v1.png|right|right|frame|Function $y = \tanh {(x)}$ <br>in tabular form.]] | [[File:P_ID3093__KC_Z_4_3neu_v1.png|right|right|frame|Function $y = \tanh {(x)}$ <br>in tabular form.]] | ||
| − | We assume a binary random variable $x ∈ \{+1, \, -1\}$ with | + | We assume a binary random variable $x ∈ \{+1, \, -1\}$ with following probabilities: |
| − | :$${\rm Pr}(x =+1) | + | :$${\rm Pr}(x =+1) = p\hspace{0.05cm},$$ |
| − | :$${\rm Pr}(x =-1) | + | :$${\rm Pr}(x =-1) = q = 1-p\hspace{0.05cm}.$$ |
| − | The "reliability" of | + | The "reliability" of symbol $x$ can be expressed |
| − | * by the | + | * by the L–value $($log likelihood ratio$)$ according to the definition |
:$$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} | :$$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * by the so called | + | * by the so called "S–value": |
:$$S(x) = p- q \hspace{0.05cm}.$$ | :$$S(x) = p- q \hspace{0.05cm}.$$ | ||
| − | We have created the term " | + | We have created the term "S–value" in order to be able to formulate the following questions more succinctly. In the literature, one sometimes finds the term "soft bit" for this. |
| − | As will be shown in subtask '''(1)''', $L(x)$ and $S(x)$ can be converted into each other. | + | As will be shown in subtask '''(1)''', $L(x)$ and $S(x)$ can be converted into each other. |
| − | Subsequently, these functions shall be used to calculate the following quantities, always assuming code length $n = 3$ | + | Subsequently, these functions shall be used to calculate the following quantities, always assuming a code length $n = 3$: |
| − | * the extrinsic | + | * the extrinsic L–value for the third symbol ⇒ $L_{\rm E}(x_3)$, |
| − | * the a posteriori& | + | |
| + | * the a-posteriori L–value for the third symbol ⇒ $L_{\rm APP}(x_3)$. | ||
The calculation should be done for the following codes: | The calculation should be done for the following codes: | ||
| − | * the repetition Code [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes|$\text{ | + | * the repetition Code [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes|$\text{RC (3, 1, 3)}$]] with the constraint $\sign {(x_1)} = \sign {(x_2)} = \sign {(x_3)}$, |
| − | * the single parity–code ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes|$\text{ | + | |
| + | * the single parity–check code ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes|$\text{SPC (3, 2, 2)}$]] with the constraint $x_1 \cdot x_2 \cdot x_3 = +1$. | ||
| Line 34: | Line 36: | ||
Hints: | Hints: | ||
* This exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder| "Soft–in Soft–out Decoder"]]. | * This exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder| "Soft–in Soft–out Decoder"]]. | ||
| − | * Reference is made in particular to the | + | |
| − | * To solve, you need the | + | * Reference is made in particular to the section [[Channel_Coding/Soft-in_Soft-Out_Decoder#Reliability_information_-_Log_Likelihood_Ratio| "Reliability Information – Log Likelihood Ratio"]]. |
| + | |||
| + | * To solve, you need the "hyperbolic tangent" according to the following definition $($this function is given above in tabular form$)$: | ||
:$$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} | :$$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} | ||
= \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} | = \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} | ||
| Line 44: | Line 48: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the relationship between | + | {What is the relationship between S–value and L–value? |
|type="[]"} | |type="[]"} | ||
- $S(x) = \tanh {(L(x))}$, | - $S(x) = \tanh {(L(x))}$, | ||
| Line 50: | Line 54: | ||
+ $L(x) = 2 \cdot \tanh^{-1}{(S(x))}$. | + $L(x) = 2 \cdot \tanh^{-1}{(S(x))}$. | ||
| − | {The $\text{RC (3, 1, 3)}$ is considered. For the | + | {The $\text{RC (3, 1, 3)}$ is considered. For the a-priori L–values, let be $\underline{L}_{\rm A} = (+2, -1, +3)$. What is the <u> extrinsicL–value</u> for the symbol $x_3$? |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ 1 3% } | $L_{\rm E}(x_3) \ = \ ${ 1 3% } | ||
| − | {What is the | + | {What is the <u>a-posteriori L–value</u> for the symbol $x_3$? |
|type="{}"} | |type="{}"} | ||
$L_{\rm APP}(x_3) \ = \ ${ 4 3% } | $L_{\rm APP}(x_3) \ = \ ${ 4 3% } | ||
| − | {What is the extrinsic | + | {What is the <u>extrinsic L–value</u> at $\text{SPC (3, 2, 2)}$? It is still valid: $\underline{L}_{\rm A} = (+2, -1, +3)$. |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ -0.757256--0.713144 } | $L_{\rm E}(x_3) \ = \ ${ -0.757256--0.713144 } | ||
| − | {The | + | {The a-priori probabilities are now $0.3, \ 0.8, \ 0.9$. What is the <u>extrinsic L–value</u> for the <u>repetition code</u>? |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ 0.535 3% } | $L_{\rm E}(x_3) \ = \ ${ 0.535 3% } | ||
| − | {What | + | {What <u>extrinsic L–value</u> results for the <u>single parity–check code</u> given the same conditions as in subtask '''(5)'''? |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(x_3) \ = \ ${ 0.49 3% } | $L_{\rm E}(x_3) \ = \ ${ 0.49 3% } | ||
Revision as of 19:07, 29 November 2022
We assume a binary random variable $x ∈ \{+1, \, -1\}$ with following probabilities:
- $${\rm Pr}(x =+1) = p\hspace{0.05cm},$$
- $${\rm Pr}(x =-1) = q = 1-p\hspace{0.05cm}.$$
The "reliability" of symbol $x$ can be expressed
- by the L–value $($log likelihood ratio$)$ according to the definition
- $$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} \hspace{0.05cm},$$
- by the so called "S–value":
- $$S(x) = p- q \hspace{0.05cm}.$$
We have created the term "S–value" in order to be able to formulate the following questions more succinctly. In the literature, one sometimes finds the term "soft bit" for this.
As will be shown in subtask (1), $L(x)$ and $S(x)$ can be converted into each other.
Subsequently, these functions shall be used to calculate the following quantities, always assuming a code length $n = 3$:
- the extrinsic L–value for the third symbol ⇒ $L_{\rm E}(x_3)$,
- the a-posteriori L–value for the third symbol ⇒ $L_{\rm APP}(x_3)$.
The calculation should be done for the following codes:
- the repetition Code $\text{RC (3, 1, 3)}$ with the constraint $\sign {(x_1)} = \sign {(x_2)} = \sign {(x_3)}$,
- the single parity–check code ⇒ $\text{SPC (3, 2, 2)}$ with the constraint $x_1 \cdot x_2 \cdot x_3 = +1$.
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the section "Reliability Information – Log Likelihood Ratio".
- To solve, you need the "hyperbolic tangent" according to the following definition $($this function is given above in tabular form$)$:
- $$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} = \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} \hspace{0.05cm}.$$
Questions
Solution
- $p = {\rm Pr}(x = +1)$, and
- $p = {\rm Pr}(x=-1) = 1-p$
the following definitions apply:
- $$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} -\infty \le L(x) \le +\infty \hspace{0.05cm},$$
- $$S(x) = p- q = 2 \cdot p - 1\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} -1 \le S(x) \le +1 \hspace{0.05cm}.$$
- Based on the $S$ value, we get because of $p + q = 1$:
- $$S(x) = p- q = \frac{p- q}{p+ q} = \frac{1- q/p}{1+ q/p} \hspace{0.05cm}.$$
- Simultaneously $q/p = {\rm e}^{-L(x)}$ holds. From this follows:
- $$S(x) = \frac{1- {\rm e}^{-L(x)}}{1+ {\rm e}^{-L(x)}} \hspace{0.05cm}.$$
- Multiplying the numerator and denominator by ${\rm e}^{-L(x)/2}$, we finally get:
- $$S(x) = \frac{{\rm e}^{+L(x)/2}- {\rm e}^{-L(x)/2}}{{\rm e}^{+L(x)/2}+ {\rm e}^{-L(x)/2}} = {\rm tanh}\big [L(x)/2. \big] \hspace{0.05cm}.$$
- The inverse function results in
- $$L(x) = 2 \cdot {\rm tanh}^{-1}[S(x)] \hspace{0.05cm}.$$
Thus, the proposed solutions 2 and 3 are correct. The table shows the $L$–value $S$–value for some probabilities $p = {\rm Pr}(x=+1)$.
(2) The extrinsic $L$ value for symbol $x_3$ considers only the apriori–$L$ values $L_{\rm A}(x_1)$ and $L_{\rm A}(x_2)$, but not $L_{\rm A}(x_3)$.
- For the (3, 1) repetition code, this results in:
- $$L_{\rm E}(x_3) = L_{\rm A}(x_1) + L_{\rm A}(x_2) = 2 + (-1) \hspace{0.15cm} \underline{= +1}\hspace{0.05cm}.$$
(3) Thus, for the aposteriori $L$ value, we obtain:
- $$L_{\rm APP}(x_3) = L_{\rm A}(x_3) + L_{\rm E}(x_3) = 3 + 1 \hspace{0.15cm} \underline{= +4}\hspace{0.05cm}.$$
(4) In the single parity–check code, the corresponding calculation rule is:
- $$L_{\rm E}(x_3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh}(x_1/2) \cdot {\rm tanh}(x_2/2) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh}(+1) \cdot {\rm tanh}(-0.5) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ 0.7616 \cdot (-0.4621) \right ] $$
- $$\Rightarrow \hspace{0.3cm}L_{\rm E}(x_3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ -0.3519 \right ] =-2 \cdot 0.3676\hspace{0.15cm} \underline{= -0.7352}\hspace{0.05cm}.$$
The result ${\rm tanh}^{-1} (-0.3519) = 0.3676$ was taken from the table on the information page.
(5) For the repetition code of length $n = 3$, the same holds as in subtask (3):
- $$L_{\rm E}(x_3) = L_{\rm A}(x_1) + L_{\rm A}(x_2) = -0.847 +1.382 \hspace{0.15cm} \underline{= +0.535}\hspace{0.05cm}.$$
The $L$ values corresponding to the table for subtask (1) were used here, for example ${\rm Pr}(x_1 = +1) = 0.3$ ⇒ $L_{\rm A}(x_1) = -0.847$.
(6) Since here instead of the apriori $L$ values the apriori probabilities are given, one comes faster to success in comparison with the subtask (4) on the detour over the extrinsic $S$ value.
- We denote the extrinsic probability for the third symbol here by $P_{\rm E}(x_3)$. For this holds:
- $$P_{\rm E}(x_3 = +1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} P_{\rm A}(x_1 = +1) \cdot P_{\rm A}(x_2 = -1) + P_{\rm A}(x_1 = -1) \cdot P_{\rm A}(x_2 = +1) = 0.3 \cdot (1-0.8) + (1-0.3) \cdot 0.8 = 0.62\hspace{0.05cm}.$$
- This results in for the further variables:
- $$S_{\rm E}(x_3) = P_{\rm E}(x_3 = +1) - P_{\rm E}(x_3 = - 1) = 0.62 -0.38 = 0.24\hspace{0.05cm},$$
- $$L_{\rm E}(x_3) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ S_{\rm E}(x_3) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} (0.24) = 2 \cdot 0.245 \hspace{0.15cm} \underline{= +0.49}\hspace{0.05cm}$$