Exercise 4.3Z: Conversions of L-value and S-value
We assume a binary random variable $x ∈ \{+1, \, -1\}$ with the following probabilities:
- $${\rm Pr}(x =+1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} p\hspace{0.05cm},$$
- $${\rm Pr}(x =-1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} q = 1-p\hspace{0.05cm}.$$
The "reliability" of the symbol $x$ can be expressed
- by the $L$ value (LLR) according to the definition
- $$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} \hspace{0.05cm},$$
- by the so called $S$ value.
- $$S(x) = p- q \hspace{0.05cm}.$$
We have created the term "$S$ value" in order to be able to formulate the following questions more succinctly. In the literature, one sometimes finds the term "soft bit" for this.
As will be shown in subtask (1), $L(x)$ and $S(x)$ can be converted into each other.
Subsequently, these functions shall be used to calculate the following quantities, always assuming code length $n = 3$ :
- the extrinsic $L$–value for the third symbol ⇒ $L_{\rm E}(x_3)$,
- the a posteriori–$L$–value for the third symbol ⇒ $L_{\rm APP}(x_3)$.
The calculation should be done for the following codes:
- the repetition Code $\text{"RC (3, 1, 3)"}$ with the constraint $\sign {(x_1)} = \sign {(x_2)} = \sign {(x_3)}$,
- the single parity–code ⇒ $\text{"SPC (3, 2, 2)"}$ with the constraint $x_1 \cdot x_2 \cdot x_3 = +1$.
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the page "Reliability Information – Log Likelihood Ratio".
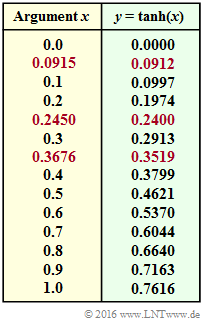
- To solve, you need the hyperbolic tangent according to the following definition (this function is given above in tabular form):
- $$y = {\rm tanh}(x) = \frac{{\rm e}^{+x/2} - {\rm e}^{-x/2}}{{\rm e}^{+x/2} + {\rm e}^{-x/2}} = \frac{1 - {\rm e}^{-x}}{1 + {\rm e}^{-x}} \hspace{0.05cm}.$$
Questions
Solution
- $p = {\rm Pr}(x = +1)$, and
- $p = {\rm Pr}(x=-1) = 1-p$
the following definitions apply:
- $$L(x) = {\rm ln} \hspace{0.2cm} \frac{p}{q} = \frac{p}{1 - p}\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} -\infty \le L(x) \le +\infty \hspace{0.05cm},$$
- $$S(x) = p- q = 2 \cdot p - 1\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} -1 \le S(x) \le +1 \hspace{0.05cm}.$$
- Based on the $S$ value, we get because of $p + q = 1$:
- $$S(x) = p- q = \frac{p- q}{p+ q} = \frac{1- q/p}{1+ q/p} \hspace{0.05cm}.$$
- Simultaneously $q/p = {\rm e}^{-L(x)}$ holds. From this follows:
- $$S(x) = \frac{1- {\rm e}^{-L(x)}}{1+ {\rm e}^{-L(x)}} \hspace{0.05cm}.$$
- Multiplying the numerator and denominator by ${\rm e}^{-L(x)/2}$, we finally get:
- $$S(x) = \frac{{\rm e}^{+L(x)/2}- {\rm e}^{-L(x)/2}}{{\rm e}^{+L(x)/2}+ {\rm e}^{-L(x)/2}} = {\rm tanh}\big [L(x)/2. \big] \hspace{0.05cm}.$$
- The inverse function results in
- $$L(x) = 2 \cdot {\rm tanh}^{-1}[S(x)] \hspace{0.05cm}.$$
Thus, the proposed solutions 2 and 3 are correct. The table shows the $L$–value $S$–value for some probabilities $p = {\rm Pr}(x=+1)$.
(2) The extrinsic $L$ value for symbol $x_3$ considers only the apriori–$L$ values $L_{\rm A}(x_1)$ and $L_{\rm A}(x_2)$, but not $L_{\rm A}(x_3)$.
- For the (3, 1) repetition code, this results in:
- $$L_{\rm E}(x_3) = L_{\rm A}(x_1) + L_{\rm A}(x_2) = 2 + (-1) \hspace{0.15cm} \underline{= +1}\hspace{0.05cm}.$$
(3) Thus, for the aposteriori $L$ value, we obtain:
- $$L_{\rm APP}(x_3) = L_{\rm A}(x_3) + L_{\rm E}(x_3) = 3 + 1 \hspace{0.15cm} \underline{= +4}\hspace{0.05cm}.$$
(4) In the single parity–check code, the corresponding calculation rule is:
- $$L_{\rm E}(x_3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh}(x_1/2) \cdot {\rm tanh}(x_2/2) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh}(+1) \cdot {\rm tanh}(-0.5) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ 0.7616 \cdot (-0.4621) \right ] $$
- $$\Rightarrow \hspace{0.3cm}L_{\rm E}(x_3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ -0.3519 \right ] =-2 \cdot 0.3676\hspace{0.15cm} \underline{= -0.7352}\hspace{0.05cm}.$$
The result ${\rm tanh}^{-1} (-0.3519) = 0.3676$ was taken from the table on the information page.
(5) For the repetition code of length $n = 3$, the same holds as in subtask (3):
- $$L_{\rm E}(x_3) = L_{\rm A}(x_1) + L_{\rm A}(x_2) = -0.847 +1.382 \hspace{0.15cm} \underline{= +0.535}\hspace{0.05cm}.$$
The $L$ values corresponding to the table for subtask (1) were used here, for example ${\rm Pr}(x_1 = +1) = 0.3$ ⇒ $L_{\rm A}(x_1) = -0.847$.
(6) Since here instead of the apriori $L$ values the apriori probabilities are given, one comes faster to success in comparison with the subtask (4) on the detour over the extrinsic $S$ value.
- We denote the extrinsic probability for the third symbol here by $P_{\rm E}(x_3)$. For this holds:
- $$P_{\rm E}(x_3 = +1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} P_{\rm A}(x_1 = +1) \cdot P_{\rm A}(x_2 = -1) + P_{\rm A}(x_1 = -1) \cdot P_{\rm A}(x_2 = +1) = 0.3 \cdot (1-0.8) + (1-0.3) \cdot 0.8 = 0.62\hspace{0.05cm}.$$
- This results in for the further variables:
- $$S_{\rm E}(x_3) = P_{\rm E}(x_3 = +1) - P_{\rm E}(x_3 = - 1) = 0.62 -0.38 = 0.24\hspace{0.05cm},$$
- $$L_{\rm E}(x_3) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ S_{\rm E}(x_3) \right ] = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} (0.24) = 2 \cdot 0.245 \hspace{0.15cm} \underline{= +0.49}\hspace{0.05cm}$$