Difference between revisions of "Aufgaben:Exercise 4.4: Pointer Diagram for DSB-AM"
m (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID718__Sig_A_4_4.png|250px|right|frame| | + | [[File:P_ID718__Sig_A_4_4.png|250px|right|frame|Spektrum des analytischen Signals]] |
Wir gehen aus von einem cosinusförmigen Quellensignal $q(t)$ mit | Wir gehen aus von einem cosinusförmigen Quellensignal $q(t)$ mit | ||
*der Amplitude $A_{\rm N} = 0.8 \ \text{V}$ und | *der Amplitude $A_{\rm N} = 0.8 \ \text{V}$ und | ||
*der Frequenz $f_{\rm N}= 10 \ \text{kHz}$. | *der Frequenz $f_{\rm N}= 10 \ \text{kHz}$. | ||
| + | |||
Die Frequenzumsetzung erfolgt mittels [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#ZSB-Amplitudenmodulation_mit_Tr.C3.A4ger|Zweiseitenband–Amplitudenmodulation mit Träger]], abgekürzt ZSB–AM. | Die Frequenzumsetzung erfolgt mittels [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#ZSB-Amplitudenmodulation_mit_Tr.C3.A4ger|Zweiseitenband–Amplitudenmodulation mit Träger]], abgekürzt ZSB–AM. | ||
| Line 27: | Line 28: | ||
| − | In der Teilaufgabe (5) ist nach dem Betrag von $s_+(t)$ gefragt. Hierunter versteht man die Länge des resultierenden Zeigers. | + | In der Teilaufgabe '''(5)''' ist nach dem Betrag von $s_+(t)$ gefragt. Hierunter versteht man die Länge des resultierenden Zeigers. |
| Line 35: | Line 36: | ||
*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Analytisches_Signal_und_zugehörige_Spektralfunktion|Analytisches Signal und zugehörige Spektralfunktion]]. | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Analytisches_Signal_und_zugehörige_Spektralfunktion|Analytisches Signal und zugehörige Spektralfunktion]]. | ||
| − | *Sie können Ihre Lösung mit dem Interaktionsmodul [[Applets: | + | *Sie können Ihre Lösung mit dem Interaktionsmodul [[Applets:Physikalisches_Signal_%26_Analytisches_Signal|Physikalisches Signal & Analytisches Signal]] überprüfen. |
| Line 89: | Line 90: | ||
*Man erhält den <u>rein reellen</u> Wert $s_+(t = 0) \;\underline{= 1.8 \ \text{V}}$. | *Man erhält den <u>rein reellen</u> Wert $s_+(t = 0) \;\underline{= 1.8 \ \text{V}}$. | ||
| − | [[File:P_ID728__Sig_A_4_4_ML.png| | + | [[File:P_ID728__Sig_A_4_4_ML.png|left|frame|Drei verschiedene analytische Signale]] |
| − | + | <br clear=all> | |
'''(2)''' Die <u>erste Aussage</u> ist richtig und ergibt sich aus der [[Signaldarstellung/Analytisches_Signal_und_zugehörige_Spektralfunktion#Darstellung_mit_der_Hilberttransformation|Hilbert-Transformation]]. Dagegen stimmen die nächsten beiden Aussagen nicht: | '''(2)''' Die <u>erste Aussage</u> ist richtig und ergibt sich aus der [[Signaldarstellung/Analytisches_Signal_und_zugehörige_Spektralfunktion#Darstellung_mit_der_Hilberttransformation|Hilbert-Transformation]]. Dagegen stimmen die nächsten beiden Aussagen nicht: | ||
| − | *$s_+(t)$ ist stets eine komplexe Zeitfunktion mit Ausnahme des Grenzfalls $s(t) = 0$. Jede komplexe Funktion hat jedoch zu einigen Zeitpunkten auch rein reelle Werte. | + | *$s_+(t)$ ist stets eine komplexe Zeitfunktion mit Ausnahme des Grenzfalls $s(t) = 0$. |
| − | *Der Zeigerverbund dreht immer in mathematisch positiver Richtung. Überschreitet der Summenvektor die reelle Achse, so verschwindet zu diesem Zeitpunkt der Imaginärteil und $s_+(t)$ ist rein reell. | + | *Jede komplexe Funktion hat jedoch zu einigen Zeitpunkten auch rein reelle Werte. |
| + | *Der Zeigerverbund dreht immer in mathematisch positiver Richtung. | ||
| + | *Überschreitet der Summenvektor die reelle Achse, so verschwindet zu diesem Zeitpunkt der Imaginärteil und $s_+(t)$ ist rein reell. | ||
| − | '''(3)''' Die Periodendauer des Trägersignals beträgt $T_0 = 1/f_T = 20 \ {\rm µ} \text{s}$. Nach $t = 5 \ {\rm µ} \text{s}$ (siehe mittlere Grafik) hat sich der Träger somit um $90^{\circ}$ gedreht. Der blaue Zeiger (OSB) dreht um 20% schneller, der grüne (USB) um 20% langsamer als der rote Drehzeiger (Trägersignal): | + | '''(3)''' Die Periodendauer des Trägersignals beträgt $T_0 = 1/f_T = 20 \ {\rm µ} \text{s}$. |
| + | *Nach $t = 5 \ {\rm µ} \text{s}$ (siehe mittlere Grafik) hat sich der Träger somit um $90^{\circ}$ gedreht. | ||
| + | *Der blaue Zeiger (OSB) dreht um 20% schneller, der grüne (USB) um 20% langsamer als der rote Drehzeiger (Trägersignal): | ||
:$$s_{+}({\rm 5 \hspace{0.05cm} {\rm µ} s}) = {\rm 1 | :$$s_{+}({\rm 5 \hspace{0.05cm} {\rm µ} s}) = {\rm 1 | ||
| Line 112: | Line 117: | ||
{\rm e}^{{\rm j}\hspace{0.05cm} 72^\circ }.$$ | {\rm e}^{{\rm j}\hspace{0.05cm} 72^\circ }.$$ | ||
| − | Somit sind die in $ 5 \ {\rm µ} \text{s}$ zurückgelegten Winkel von OSB und USB $108^{\circ}$ bzw. $72^{\circ}$. Da sich zu diesem Zeitpunkt die Realteile von OSB und USB kompensieren, ist $s_+(t=5 \ {\rm µ} \text{s})$ <u>rein imaginär</u> und man erhält: | + | *Somit sind die in $ 5 \ {\rm µ} \text{s}$ zurückgelegten Winkel von OSB und USB $108^{\circ}$ bzw. $72^{\circ}$. |
| + | *Da sich zu diesem Zeitpunkt die Realteile von OSB und USB kompensieren, ist $s_+(t=5 \ {\rm µ} \text{s})$ <u>rein imaginär</u> und man erhält: | ||
:$${\rm Im}\left[s_{+}(t = {\rm 5 \hspace{0.05cm} {\rm µ} s})\right] = | :$${\rm Im}\left[s_{+}(t = {\rm 5 \hspace{0.05cm} {\rm µ} s})\right] = | ||
| Line 132: | Line 138: | ||
Innerhalb einer Periode $T_0$ des Trägers tritt gegenüber den Zeigern der beiden Seitenbändern ein Phasenversatz von $\pm72^{\circ}$ auf. Daraus folgt: | Innerhalb einer Periode $T_0$ des Trägers tritt gegenüber den Zeigern der beiden Seitenbändern ein Phasenversatz von $\pm72^{\circ}$ auf. Daraus folgt: | ||
| − | :$$t_{\text{min}} = 2.5 \cdot T_0 \;\underline{= 50 \ {\rm µ} \text{s}}.$$ | + | :$$t_{\text{min}} = 180^{\circ}/72^{\circ} \cdot T_0 = 2.5 \cdot T_0 \;\underline{= 50 \ {\rm µ} \text{s}}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | [[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | ||
Revision as of 10:38, 26 July 2018
Wir gehen aus von einem cosinusförmigen Quellensignal $q(t)$ mit
- der Amplitude $A_{\rm N} = 0.8 \ \text{V}$ und
- der Frequenz $f_{\rm N}= 10 \ \text{kHz}$.
Die Frequenzumsetzung erfolgt mittels Zweiseitenband–Amplitudenmodulation mit Träger, abgekürzt ZSB–AM.
Das modulierte Signal $s(t)$ lautet mit dem (normierten) Träger $z(t) = \text{cos}(\omega_{\rm T} \cdot t)$ und dem Gleichanteil $q_0 = 1 \ \text{V}$:
- $$\begin{align*} s(t) & = \left(q_0 + q(t)\right) \cdot z(t)= \left({\rm 1 \hspace{0.05cm} V} + {\rm 0.8 \hspace{0.05cm}V}\cdot {\cos} ( \omega_{\rm N}\cdot t)\right) \cdot {\cos} ( \omega_{\rm T}\cdot t) = \\ & = q_0 \cdot {\cos} ( \omega_{\rm T}\cdot t) + {A_{\rm N}}/{2} \cdot {\cos} ( (\omega_{\rm T}+ \omega_{\rm N}) \cdot t) + {A_{\rm N}}/{2} \cdot {\cos} ( (\omega_{\rm T}- \omega_{\rm N}) \cdot t).\end{align*}$$
Der erste Term beschreibt den Träger, der zweite Term das sogenannte obere Seitenband (OSB) und der letzte Term das untere Seitenband (USB).
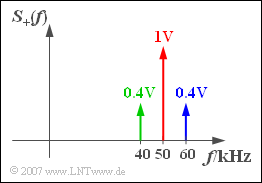
Die Skizze zeigt das Spektrum $S_+(f)$ des dazugehörigen analytischen Signals für $f_{\rm T} = 50 \ \text{kHz}$. Man erkennt
- den Träger (rot),
- das obere Seitenband (blau) und
- das untere Seitenband (grün).
In der Teilaufgabe (5) ist nach dem Betrag von $s_+(t)$ gefragt. Hierunter versteht man die Länge des resultierenden Zeigers.
Hinweise:
- Die Aufgabe gehört zum Kapitel Analytisches Signal und zugehörige Spektralfunktion.
- Sie können Ihre Lösung mit dem Interaktionsmodul Physikalisches Signal & Analytisches Signal überprüfen.
Fragebogen
Musterlösung
- $$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 50}\hspace{0.05cm} t } + {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 60} \hspace{0.05cm} t }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 40}\hspace{0.05cm} t }.$$
Der Ausdruck beschreibt die Summe dreier Zeiger, die mit unterschiedlichen Winkelgeschwindigkeiten drehen.
- In obiger Gleichung bedeutet beispielsweise $\omega_{60} = 2\pi (f_{\rm T} + f_{\rm N}) = 2\pi \cdot 60 \ \text{kHz}$.
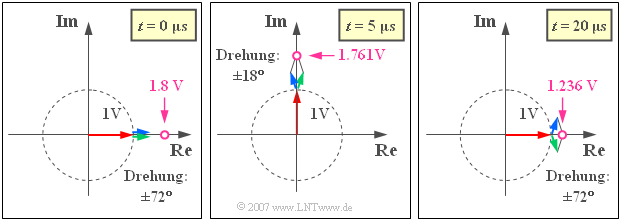
- Zum Zeitpunkt $t = 0$ zeigen alle drei Zeiger in Richtung der reellen Achse (siehe linke Grafik).
- Man erhält den rein reellen Wert $s_+(t = 0) \;\underline{= 1.8 \ \text{V}}$.
(2) Die erste Aussage ist richtig und ergibt sich aus der Hilbert-Transformation. Dagegen stimmen die nächsten beiden Aussagen nicht:
- $s_+(t)$ ist stets eine komplexe Zeitfunktion mit Ausnahme des Grenzfalls $s(t) = 0$.
- Jede komplexe Funktion hat jedoch zu einigen Zeitpunkten auch rein reelle Werte.
- Der Zeigerverbund dreht immer in mathematisch positiver Richtung.
- Überschreitet der Summenvektor die reelle Achse, so verschwindet zu diesem Zeitpunkt der Imaginärteil und $s_+(t)$ ist rein reell.
(3) Die Periodendauer des Trägersignals beträgt $T_0 = 1/f_T = 20 \ {\rm µ} \text{s}$.
- Nach $t = 5 \ {\rm µ} \text{s}$ (siehe mittlere Grafik) hat sich der Träger somit um $90^{\circ}$ gedreht.
- Der blaue Zeiger (OSB) dreht um 20% schneller, der grüne (USB) um 20% langsamer als der rote Drehzeiger (Trägersignal):
- $$s_{+}({\rm 5 \hspace{0.05cm} {\rm µ} s}) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}50 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } + {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}60 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}40 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 90^\circ }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 108^\circ }+{\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 72^\circ }.$$
- Somit sind die in $ 5 \ {\rm µ} \text{s}$ zurückgelegten Winkel von OSB und USB $108^{\circ}$ bzw. $72^{\circ}$.
- Da sich zu diesem Zeitpunkt die Realteile von OSB und USB kompensieren, ist $s_+(t=5 \ {\rm µ} \text{s})$ rein imaginär und man erhält:
- $${\rm Im}\left[s_{+}(t = {\rm 5 \hspace{0.05cm} {\rm µ} s})\right] = {\rm 1 \hspace{0.05cm} V} + 2 \cdot {\rm 0.4 \hspace{0.05cm} V}\cdot \cos (18^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.761 \hspace{0.05cm} V}}.$$
(4) Nach einer Umdrehung des roten Trägers, also zum Zeitpunkt $t$ = $T_0 = 20 \ {\rm µ} \text{s}$ hat der blaue Zeiger bereits $72^{\circ}$ mehr zurückgelegt und der grüne Zeiger dementsprechend $72^{\circ}$ weniger. Die Summe der drei Zeiger ist wieder rein reell und ergibt entsprechend der rechten Grafik:
- $${\rm Re}\left[s_{+}({\rm 20 \hspace{0.05cm} {\rm µ} s})\right] = {\rm 1 \hspace{0.05cm} V} + 2 \cdot {\rm 0.4 \hspace{0.05cm} V}\cdot \cos (72^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.236 \hspace{0.05cm} V}}.$$
(5) Der Betrag ist minimal, wenn die Zeiger der beiden Seitenbänder gegenüber dem Träger um $180^{\circ}$ versetzt sind. Daraus folgt:
- $$|s_{+}(t)|_{\rm min} = {\rm 1 \hspace{0.05cm} V} - 2 \cdot {\rm 0.4 \hspace{0.05cm} V} \hspace{0.15 cm}\underline{= {\rm 0.2 \hspace{0.05cm} V}}.$$
Innerhalb einer Periode $T_0$ des Trägers tritt gegenüber den Zeigern der beiden Seitenbändern ein Phasenversatz von $\pm72^{\circ}$ auf. Daraus folgt:
- $$t_{\text{min}} = 180^{\circ}/72^{\circ} \cdot T_0 = 2.5 \cdot T_0 \;\underline{= 50 \ {\rm µ} \text{s}}.$$