Exercise 4.4Z: Signal-to-Noise Ratio with PCM

• Return to book

Sink-to-drop ratio of PCM 30/32 compared to ZSB amplitude modulation

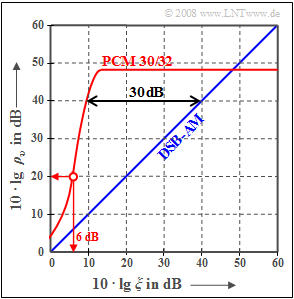
The graph shows the sink-to-noise ratio  $10 - \lg \ ρ_v$  for pulse code modulation  $\rm (PCM)$  compared to analog double-sideband amplitude modulation, abbreviated as  $\rm ZSB-AM$. 

For the latter,  $ρ_v = ξ$, where the power parameter.

$$\xi = \frac{\alpha^2 \cdot P_{\rm S}}{N_0 \cdot f_{\rm N}} $$

Summarizes the following system parameters:

• the frequency-independent transmission factor  $α$  of the transmission channel,
• the power  $P_{\rm S}$  of the transmit signal  $s(t)$, also called transmit power for short,
• the message frequency  $f_{\rm N}$  (bandwidth) of the cosine source signal  $q(t)$,
• the noise power density  $N_0$  of the AWGN noise.

For the PCM system, the following approximation for the sink SNR was given on the page  Estimation of SNR degradation due to bit errors  which also takes into account transmission errors due to AWGN noise:

$$ \rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$

• Here  $N$  denotes the number of bits per sample and  $p_{\rm B}$  the bit error probability.
• Since  $ξ$  in digital modulation can also be interpreted as the signal energy per bit  related to the noise power density $(E_{\rm B}/N_0)$, with the complementary Gaussian error signal  ${\rm Q}(x)$  approximately:

$$ p_{\rm B}= {\rm Q} \left ( \sqrt{2 \xi }\right ) \hspace{0.05cm}.$$

Hints:

• The exercise belongs to the chapter  Pulse Code Modulation.
• Reference is made in particular to the pages  Influence of transmission errors  and  Estimation of SNR degradation by bit errors.
• The PCM considered here is the  PCM 30/32 whose system parameters are given, for example, in the  Exercise 4.1 .

Questions

1

Wieviele Bit pro Abtastwert   ⇒   $N = N_1$  verwendet das betrachtete PCM–System?

$N_1 \ = \ $

2

Wieviele Bit pro Abtastwert   ⇒   $N = N_2$  müsste man verwenden, damit  $10 · \lg \ ρ_v > 64 \ \rm dB$  (Musikqualität) erreicht wird?

$N_2 \ = \ $

3

Welche (logarithmierte) Leistungskenngröße  $ξ_{40\ \rm dB}$  ist erforderlich, damit bei 8–Bit–PCM der Sinkenstörabstand gleich  $40\ \rm dB$  ist?

$10 · \lg \ ξ_{40\ \rm dB} \ = \ $ $\ \rm dB$

4

Um welchen Faktor könnte man bei PCM die Sendeleistung gegenüber der ZSB–AM reduzieren, um trotzdem  $10 · \lg \ ρ_v = 40\ \rm dB$  zu erreichen?

$K_\text{AM → PCM} \ = \ $

5

Welche Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  ergibt sich für  $10 · \lg \ ξ = 6\ \rm dB$  und  $N = N_1$   ⇒   Ergebnis der Teilaufgabe  (1)?

$p_{\rm B} \ = \ $ $\ \%$

6

Welches SNR würde sich bei gleichem  $ξ$  mit einer 3–Bit–PCM   ⇒   $N = 3$  ergeben?

$10 · \lg \ ρ_v \ = \ $ $\ \rm dB$

Musterlösung

Solution

(1)  Der horizontale Abschnitt der PCM–Kurve wird allein durch das Quantisierungsrauschen bestimmt. 

• Hier gilt mit der Quantisierungsstufenzahl  $M = 2^N$:

$$ \rho_{v} (\xi \rightarrow \infty) = \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{v} \approx 6\,{\rm dB} \cdot N\hspace{0.05cm}.$$

• Aus dem ablesbaren Störabstand  $10 · \lg \ ρ_v ≈ 48 \ \rm dB$  folgt daraus  $N_1\hspace{0.15cm}\underline { = 8}$  Bit pro Abtastwert und für die Quantisierungsstufenzahl  $M = 256$.

(2)  Aus der obigen Näherung erhält man für  $N_2\hspace{0.15cm}\underline { = 11}$  Bit pro Abtastwert   ⇒   $M = 2048$  den Störabstand  $66 \ \rm dB$.

• Mit  $N = 10$   ⇒   $M = 1024$  erreicht man nur ca.  $60 \ \rm dB$.
• Bei der Compact Disc (CD) werden die PCM–Parameter  $N = 16$   ⇒   $M = 65536$   ⇒   $10 · \lg \ ρ_v > 96 \ \rm dB$  verwendet.

(3)  Bei Zweiseitenband–Amplitudenmodulation wären hierfür  $10 · \lg \ ξ = 40\ \rm dB$  erforderlich.

• Wie aus der Grafik auf der Angabenseite hervorgeht, ist dieser Abszissenwert für die vorgegebene PCM um  $30 \ \rm dB$  geringer   ⇒   $10 · \lg \ ξ_{40\ \rm dB}\hspace{0.15cm}\underline { = 10 \ \rm dB}$.

(4)  Der logarithmische Wert  $30 \ \rm dB$  entspricht einer um den Faktor  $10^3\hspace{0.15cm}\underline { = 1000}$  reduzierten Leistung.

(5)  Aus der Grafik auf der Angabenseite erkennt man, dass der Abszissenwert  $10 · \lg \ ξ= 6 \ \rm dB$  den Störabstand  $20 \ \rm dB$  zur Folge hat.

• Aus  $10 · \lg \ ρ_v = 20 \ \rm dB$  folgt  $ρ_v = 100$  und damit weiter  $($mit  $N = N_1 = 8)$:

$$\rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \approx \frac{1}{ 1.5 \cdot 10^{-5} + 4 \cdot p_{\rm B}} = 100 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} = \frac{0.01 - 1.5 \cdot 10^{-5}}{ 4} \hspace{0.15cm}\underline {\approx 2.5\%} \hspace{0.05cm}.$$

(6)  Bei gleichem  $ξ$  ist die Bitfehlerwahrscheinlichkeit weiterhin  $p_{\rm B} = 0.025$.  Damit erhält man mit  $N = 3$  (Bit pro Abtastwert):

$$\rho_{\upsilon}= \frac{1}{ 2^{-6 } + 4 \cdot p_{\rm B}} = \frac{1}{ 0.015625 + 0.01} \approx 39 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\upsilon}\hspace{0.15cm}\underline {\approx 15.9\,{\rm dB}} \hspace{0.05cm}.$$

Weiter ist anzumerken:

• Bei nur drei Bit pro Abtastwert ist die Quantisierungsrauschleistung  $(P_{\rm Q} = 0.015625)$  schon größer als die Fehlerrauschleistung  $(P_{\rm F} = 0.01)$.
• Durch Erhöhung der Sendeleistung könnte wegen der Quantisierung der Sinkenstörabstand maximal  $10 · \lg \ ρ_v =18 \ \rm dB$  betragen, wenn keine Bitfehler vorkommen  $(P_{\rm F} = 0)$.