Exercise 4.5: Coaxial Cable - Impulse Response
From LNTwww
- Der Frequenzgang eines Koaxialkabels der Länge l ist durch folgende Formel darstellbar:
- $$H_{\rm K}(f) = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} \cdot \\ \cdot {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot \\ \cdot {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
- Der erste Term dieser Gleichung ist auf die Ohmschen Verluste zurückzuführen und der zweite Term auf die Querverluste. Dominant ist jedoch der Skineffekt, der durch den dritten Term ausgedrückt wird.
- Mit den für ein so genanntes Normalkoaxialkabel (2.6 mm Kerndurchmesser und 9.5 mm Außendurchmesser) gültigen Koeffizienten
- $$\alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} \hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722 \hspace{0.15cm}\frac {\rm rad}{\rm km \cdot \sqrt{\rm MHz}}\hspace{0.05cm}$$
- lässt sich dieser Frequenzgang auch wie folgt darstellen:
- $$H_{\rm K}(f) \approx {\rm e}^{- 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}} } \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} \hspace{0.05cm}.$$
- Das heißt: Der Dämpfungsverlauf aK(f) und der Phasenverlauf bK(f) sind bis auf die Pseudoeinheiten „Np” bzw. „rad” identisch.
- Definiert man die charakteristische Kabeldämpfung a∗ bei der halben Bitrate (also bei R/2), so kann man Digitalsysteme unterschiedlicher Bitrate und Länge einheitlich behandeln:
- $${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f ={R}/{2}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- {\rm a}_{\rm \star} \cdot \sqrt{2f/R}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} {\rm a}_{\rm \star} \cdot \sqrt{2f/R}}\hspace{0.4cm}{\rm mit}\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
- Der entsprechende dB–Wert ist um den Faktor 8.686 größer. Bei einem Binärsystem gilt R = 1/T, so dass sich die charakteristische Kabeldämpfung auf die Frequenz f = 1/(2T) bezieht.
- Die Fouriertransformierte von HK(f) liefert die Impulsantwort hK(t), die für ein Koaxialkabel mit den hier beschriebenen Näherungen in geschlossen–analytischer Form angebbar ist. Für ein Binärsystem gilt:
- $$h_{\rm K}(t) = \frac{ {\rm a}_{\rm \star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{{\rm a}_{\rm \star}^2}{2 \pi \cdot t/T}\hspace{0.1cm}\right] \hspace{0.4cm}{\rm mit}\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
- Die Teilaufgabe 5) bezieht sich auf den Empfangsgrundimpuls gr(t) = gs(t) ∗ hK(t), wobei für gs(t) ein Rechteckimpuls mit der Höhe s0 und der Dauer T angenommen werden soll.
- Hinweis: Die Aufgabe gehört zu Kapitel 4.2 des vorliegenden Buches. Sie können zur Überprüfung Ihrer Ergebnisse das folgende Interaktionsmodul benutzen:
- Dämpfung von Kupferkabeln
Fragebogen
Musterlösung
- 1. Die charakteristische Kabeldämpfung a∗ = 60 dB entspricht in etwa 6.9 Np. Deshalb muss gelten:
- $$\alpha_2 \cdot l \cdot \frac{R}{2} = 6.9\,\,{\rm Np} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} l = \frac{6.9\,\,{\rm Np}}{0.2722 \,\,\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} \cdot \sqrt{70\,\,{\rm MHz}}}\hspace{0.15cm}\underline{ \approx 3\,\,{\rm km}} \hspace{0.05cm}.$$
- 2. Mit den Substitutionen
- $$x = \frac{ t}{ T}, \hspace{0.2cm} K_1 = \frac{ {\rm a}_{\rm \star}/T}{\sqrt{2 \pi^2 }}, \hspace{0.2cm} K_2 = \frac{ {\rm a}_{\rm \star}^2}{2 \pi}$$
- kann die Impulsantwort wie folgt beschrieben werden:
- $$h_{\rm K}(x) = K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x} \hspace{0.05cm}.$$
- Durch Nullsetzen der Ableitung folgt daraus:
- $$- \frac{3}{2} \cdot K_1 \cdot x^{-5/2}\cdot {\rm e}^{-K_2/x}+ K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x}\cdot (-K_2) \cdot (-x^{-2})= 0 \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm} \frac{3}{2} \cdot x^{-5/2} = K_2 \cdot x^{-7/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x_{\rm max} = \frac{2}{3} \cdot K_2 = \frac{{\rm a}_{\rm \star}^2}{3 \pi} \hspace{0.05cm}.$$
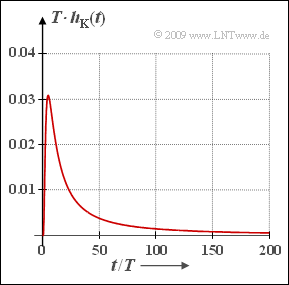
- Daraus ergibt sich für 60 dB Kabeldämpfung (a∗ ≈ 6.9 Np):
- $$x_{\rm max} = { t_{\rm max}}/{ T}= { 6.9^2}/{(3\pi)}\hspace{0.15cm}\underline{ \approx 5 }\hspace{0.05cm} .$$
- 3. Setzt man das Ergebnis von b) in die vorgegebene Gleichung ein, so erhält man (zur Vereinfachung verwenden wir a anstelle von a∗):
- $$h_{\rm K}(t_{\rm max}) = \frac{1}{T} \cdot \frac{ {\rm a}}{ \sqrt{2 \pi^2 \cdot \frac{{\rm a}^6}{(3\pi)^3}}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{{\rm a}^2}{2\pi} \cdot \frac{3\pi}{{\rm a}^2}\hspace{0.1cm}\right]\\ = \frac{1}{T} \cdot \frac{1}{{\rm a}^2}\cdot \sqrt{\frac{27 \pi }{2}} \cdot {\rm e}^{-3/2} \approx \frac{1}{T} \cdot \frac{1.453}{{\rm a}^2} \hspace{0.05cm}.$$
- Mit a = 6.9 kommt man somit zum Endergebnis:
- $${\rm Max}[h_{\rm K}(t)] = \frac{1.453}{{6.9\,}^2} \cdot {1}/{T}\hspace{0.15cm}\underline{\approx 0.03 \cdot {1}/{T}} \hspace{0.05cm}.$$
- 4. Mit dem Ergebnis aus 3) lautet die Bestimmungsgleichung:
- $$\frac{ {\rm a}/T}{ \sqrt{2 \pi^2 \cdot (t_{5\%}/T)^3}}= 0.05 \cdot 0.03 {1}/{T} \hspace{0.15cm}{= 0.0015 \cdot {1}/{T}}$$
- $$\Rightarrow \hspace{0.3cm} (t_{5\%}/T)^{3/2} = \frac{\rm a}{\sqrt{2} \cdot \pi \cdot 0.0015}\approx 1036 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{t_{5\%}/T \approx 103.5} \hspace{0.05cm}.$$
- Dieser Wert ist etwas zu groß, da der zweite Term e– 0.05 ≈ 0.95 vernachlässigt wurde. Die exakte Berechnung liefert t5%/T ≈ 97.
- 5. Richtig ist der zweite Lösungsvorschlag. Allgemein gilt:
- $$g_r(t) = g_s(t) \star h_{\rm K}(t) = s_0 \cdot \int\limits_{t-T/2}^{t+T/2} h_{\rm K}(\tau) \,{\rm d} \tau .$$
- Da sich die Kanalimpulsantwort hK(t) innerhalb einer Symboldauer nur unwesentlich ändert, kann hierfür auch geschrieben werden:
- $$g_r(t) = h_{\rm K}(t) \cdot s_0 \cdot T .$$