Difference between revisions of "Aufgaben:Exercise 4.5: Two-dimensional Examination Evaluation"
From LNTwww
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables |
}} | }} | ||
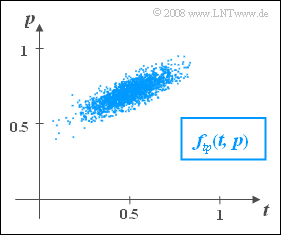
| − | [[File:P_ID267__Sto_A_4_5.png|right|frame| | + | [[File:P_ID267__Sto_A_4_5.png|right|frame|Applied Gaussian 2D PDF $f_{tp}(t,p)$]] |
| − | In | + | In a study, the master craftsman examinations were investigated, which always consist of a theoretical and additionally a practical part. In the graph denoted |
| − | * $t$ | + | * $t$ denotes the score in the theoretical test, |
| − | * $p$ | + | * $p$ the score in the practical test. |
| − | + | Both random variables $(t$ and $p)$ are normalized to the maximum scores and can therefore only take values between $0$ and $1$ . | |
| − | + | Moreover, both random variables are to be interpreted as continuous random variables, i.e.: $t$ and $p$ are not restricted to discrete numerical values. | |
| − | * | + | *The graph shows the PDF $f_{tp}(t, p)$ of the two-dimensional random variable $(t, p)$, which was published after evaluating a total of $N = 10\hspace{0.08cm}000$ final papers. |
| − | * | + | *This function was empirically approximated using an evaluation program as follows: |
:$$f_{tp}(t,p) = \rm 13.263\cdot \rm exp \Bigg\{-\frac{(\it t - \rm 0.5)^{\rm 2}}{\rm 0.0288}-\frac{(\it p-\rm 0.7)^{\rm 2}}{\rm 0.0072} + \frac{(\it t-\rm 0.5)(\it p-\rm 0.7)}{\rm 0.0090}\Bigg\}.$$ | :$$f_{tp}(t,p) = \rm 13.263\cdot \rm exp \Bigg\{-\frac{(\it t - \rm 0.5)^{\rm 2}}{\rm 0.0288}-\frac{(\it p-\rm 0.7)^{\rm 2}}{\rm 0.0072} + \frac{(\it t-\rm 0.5)(\it p-\rm 0.7)}{\rm 0.0090}\Bigg\}.$$ | ||
| Line 24: | Line 24: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables|Two-dimensional Gaussian Random Variables]]. |
| − | + | ||
| − | * | + | *More information on this topic is provided in the learning video [[Gaußsche_2D-Zufallsgrößen_(Lernvideo)|Gaussian 2D random variables]]: |
| − | :: | + | ::Part 1: Gaussian random variables without statistical bindings, |
| − | :: | + | ::Part 2: Gaussian random variables with statistical bindings. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the mean value $m_t$ of the results obtained in the theory part? |
|type="{}"} | |type="{}"} | ||
$m_t \ = \ $ { 0.5 3% } | $m_t \ = \ $ { 0.5 3% } | ||
| − | { | + | {What is the mean $m_p$ of the results obtained in the practice part? Give also the PDF of the zero mean random variable $(t\hspace{0.05cm}', p\hspace{0.05cm}')$ . |
|type="{}"} | |type="{}"} | ||
| − | $m_p \ = | + | $m_p \ = \ $ { 0.7 3% } |
| − | { | + | {Calculate the standard deviations $\sigma_t$ and $\sigma_p$ as well as the correlation coefficient $\rho$ between the two sizes. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_t \ = | + | $\sigma_t \ = \ $ { 0.2 3% } |
| − | $\sigma_p \ = | + | $\sigma_p \ = \ $ { 0.1 3% } |
| − | $\rho \ = | + | $\rho \ = \ $ { 0.8 3% } |
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The Gaussian approach is only an approximation for this problem. |
| − | - | + | - If an examinee was above average in the theory part, it is to be expected that he is rather bad in practice. |
| − | + | {What is the probability that a participant scored between $49\%$ and $51\%$ of the points in the theory– and the practice–exam respectively? | |
| − | |||
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}\big [(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big]\ = | + | ${\rm Pr}\big [(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big]\ = \ $ { 2 3% } $\ \cdot 10^{-5}$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' and '''(2)''' |
| − | * | + | *The mean values $m_t\hspace{0.15cm}\underline{= 0.5}$ and $m_p\hspace{0.15cm}\underline{= 0.7}$ can be estimated from the sketch and obtained exactly from the given equation. |
| − | * | + | *The 2D PDF of the zero mean variable is: |
:$$f_{\it t\hspace{0.05cm}'\hspace{0.05cm}p\hspace{0.05cm}'}(\it t\hspace{0.05cm}', \it p\hspace{0.05cm}'{\rm )} = \rm 13.263\cdot \rm exp\Bigg (-\frac{\it {\rm (}t\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0288} - \frac{\it {\rm (}p\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0072}+\frac{\it t\hspace{0.05cm}'\cdot p\hspace{0.05cm}'}{\rm 0.0090}\Bigg ). $$ | :$$f_{\it t\hspace{0.05cm}'\hspace{0.05cm}p\hspace{0.05cm}'}(\it t\hspace{0.05cm}', \it p\hspace{0.05cm}'{\rm )} = \rm 13.263\cdot \rm exp\Bigg (-\frac{\it {\rm (}t\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0288} - \frac{\it {\rm (}p\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0072}+\frac{\it t\hspace{0.05cm}'\cdot p\hspace{0.05cm}'}{\rm 0.0090}\Bigg ). $$ | ||
| − | * | + | *For simplicity, the apostrophe is omitted below to denote zero mean variables. |
| − | * | + | *Both $t$ and $p$ are to be understood as zero mean up to and including the subtask '''(4)'''' . |
| − | '''(3)''' | + | '''(3)''' The general equation of a zero mean 2D random variable is: |
:$$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 2\it \pi \cdot \sigma_{\it t}\cdot \sigma_{\it p} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 2\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it t}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{ (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it t}\cdot\sigma_{\it p}}\Bigg\}.$$ | :$$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 2\it \pi \cdot \sigma_{\it t}\cdot \sigma_{\it p} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 2\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it t}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{ (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it t}\cdot\sigma_{\it p}}\Bigg\}.$$ | ||
| − | * | + | |
| − | * | + | *The standard deviations $\sigma_t$ and $\sigma_p$ as well as the correlation coefficient $\rho$ can be obtained by coefficient comparison: |
| + | *A comparison of the first two terms in the exponent shows that $\sigma_t = 2 \cdot \sigma_p$ must hold. Thus the PDF is: | ||
:$$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 4\it \pi \cdot \sigma_{\it p}^{\rm 2} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 8\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it p}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{\rm 2\cdot (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it p}^{\rm 2}}\Bigg\}.$$ | :$$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 4\it \pi \cdot \sigma_{\it p}^{\rm 2} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 8\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it p}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{\rm 2\cdot (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it p}^{\rm 2}}\Bigg\}.$$ | ||
| − | * | + | *From the second term of the exponent follows: |
:$$2\cdot(1-\rho^{\rm 2})\cdot\sigma_{p}^{ 2}=0.0072\hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{p}^{2} = \frac{ 0.0036}{(1-\rho^{\rm 2})}.$$ | :$$2\cdot(1-\rho^{\rm 2})\cdot\sigma_{p}^{ 2}=0.0072\hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{p}^{2} = \frac{ 0.0036}{(1-\rho^{\rm 2})}.$$ | ||
| − | * | + | *The factor $K = 13.263$ now gives the result. |
:$$K = \frac{\sqrt{\rm 1-\it\rho^{\rm 2}}}{\rm 4\it\pi\cdot \rm 0.0036}=\rm 13.263 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sqrt{\rm 1-\it\rho^{\rm 2}}=\rm 0.6 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\hspace{0.15cm}\underline{ \rm \rho = \rm 0.8}.$$ | :$$K = \frac{\sqrt{\rm 1-\it\rho^{\rm 2}}}{\rm 4\it\pi\cdot \rm 0.0036}=\rm 13.263 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sqrt{\rm 1-\it\rho^{\rm 2}}=\rm 0.6 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\hspace{0.15cm}\underline{ \rm \rho = \rm 0.8}.$$ | ||
| − | * | + | *From this we get the standard deviations to $\sigma_t\hspace{0.15cm}\underline{= 0.2}$ and $\sigma_p\hspace{0.15cm}\underline{= 0.1}$. |
| − | * | + | *For control, we use the last term of the exponent: |
| − | :$$\frac{(1 - \rho^{2})\cdot | + | :$$\frac{(1 - \rho^{2})\cdot \sigma_{\it t}\cdot\sigma_{\it p}}{\it \rho} = \frac{0.36\cdot 0.1\cdot 0.2}{0.8} = \rm 0.009.$$ |
| − | * | + | *This agrees with the given value. |
| − | |||
| − | '''(4)''' | + | '''(4)''' The <u>proposed solution 1</u> is correct. |
| − | * | + | *Basically, $(t, p)$ is not a true Gaussian random variable, since both components are bounded. |
| − | * | + | *The probabilities for the events $t < 0$, $t >1$, $p < 0$ and $p >1$ are therefore zero. |
| − | * | + | *However, for Gaussian variables with the mean values and standard deviations present here, we get. |
:$$\rm Pr(\it t < \rm 0) = \rm Pr(\it t > \rm 1) = \rm Q(2.5)\approx 6\cdot 10^{-3},$$ | :$$\rm Pr(\it t < \rm 0) = \rm Pr(\it t > \rm 1) = \rm Q(2.5)\approx 6\cdot 10^{-3},$$ | ||
:$$\rm Pr(\it p > \rm 1) = \rm Q(3)\approx 1.3\cdot 10^{-3},$$ | :$$\rm Pr(\it p > \rm 1) = \rm Q(3)\approx 1.3\cdot 10^{-3},$$ | ||
:$$\rm Pr(\it p < \rm 0) = \rm Q(7)\approx 10^{-12}.$$ | :$$\rm Pr(\it p < \rm 0) = \rm Q(7)\approx 10^{-12}.$$ | ||
| − | * | + | *The correlation coefficient $\rho = 0.8$ is positive here. If the examinee has done rather well in the theory part, it is to be expected (at least for this exercise) that the practical part will also go well. |
| − | * | + | *Suggestion 2 is therefore wrong here. In practice, this is certainly not always the case. |
| − | '''(5)''' | + | '''(5)''' For this probability, $\Delta t = \Delta p = 0.02$: |
| − | :$$\rm Pr\left [( \rm 0.5-\frac{\rm\Delta\it t}{\rm 2}\le \it t \le \rm 0.5+\frac{\rm\Delta\it t}{\rm 2})\cap(\rm 0.5-\frac{\rm\ | + | :$$\rm Pr\left [( \rm 0.5-\frac{\rm\Delta\it t}{\rm 2}\le \it t \le \rm 0.5+\frac{\rm\Delta\it t}{\rm 2})\cap(\rm 0. 5-\frac{\rm\delta\it p}{\rm 2}\le \it p \le \rm 0.5+\frac{\rm\delta\it p}{\rm 2})\right ] \approx \rm\Delta\it t\cdot\rm\Delta\it p\cdot \it f_{tp}{\rm (}t=\rm 0.5, \it p = \rm 0.5).$$ |
| − | * | + | *For the 2D PDF, taking into account the mean values $m_t{= 0.5}$ and $m_p{= 0.7}$: |
:$$f_{tp}(\it t=\rm 0.5, \it p=\rm 0.5) = \rm 13.263\cdot {\rm e}^{-(-0.2)^2/0.0072}\approx 0.0513.$$ | :$$f_{tp}(\it t=\rm 0.5, \it p=\rm 0.5) = \rm 13.263\cdot {\rm e}^{-(-0.2)^2/0.0072}\approx 0.0513.$$ | ||
| − | * | + | *Thus, the probability we are looking for is given by |
| − | :$${\rm Pr}\big[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big] = | + | :$${\rm Pr}\big[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big] =0.02 \cdot 0.0513\hspace{0.15cm}\underline{\approx 2 · 10^{-5}}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 23:56, 23 January 2022
In a study, the master craftsman examinations were investigated, which always consist of a theoretical and additionally a practical part. In the graph denoted
- $t$ denotes the score in the theoretical test,
- $p$ the score in the practical test.
Both random variables $(t$ and $p)$ are normalized to the maximum scores and can therefore only take values between $0$ and $1$ .
Moreover, both random variables are to be interpreted as continuous random variables, i.e.: $t$ and $p$ are not restricted to discrete numerical values.
- The graph shows the PDF $f_{tp}(t, p)$ of the two-dimensional random variable $(t, p)$, which was published after evaluating a total of $N = 10\hspace{0.08cm}000$ final papers.
- This function was empirically approximated using an evaluation program as follows:
- $$f_{tp}(t,p) = \rm 13.263\cdot \rm exp \Bigg\{-\frac{(\it t - \rm 0.5)^{\rm 2}}{\rm 0.0288}-\frac{(\it p-\rm 0.7)^{\rm 2}}{\rm 0.0072} + \frac{(\it t-\rm 0.5)(\it p-\rm 0.7)}{\rm 0.0090}\Bigg\}.$$
Hints:
- The exercise belongs to the chapter Two-dimensional Gaussian Random Variables.
- More information on this topic is provided in the learning video Gaussian 2D random variables:
- Part 1: Gaussian random variables without statistical bindings,
- Part 2: Gaussian random variables with statistical bindings.
Questions
Solution
(1) and (2)
- The mean values $m_t\hspace{0.15cm}\underline{= 0.5}$ and $m_p\hspace{0.15cm}\underline{= 0.7}$ can be estimated from the sketch and obtained exactly from the given equation.
- The 2D PDF of the zero mean variable is:
- $$f_{\it t\hspace{0.05cm}'\hspace{0.05cm}p\hspace{0.05cm}'}(\it t\hspace{0.05cm}', \it p\hspace{0.05cm}'{\rm )} = \rm 13.263\cdot \rm exp\Bigg (-\frac{\it {\rm (}t\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0288} - \frac{\it {\rm (}p\hspace{0.05cm}'{\rm )}^{\rm 2}}{\rm 0.0072}+\frac{\it t\hspace{0.05cm}'\cdot p\hspace{0.05cm}'}{\rm 0.0090}\Bigg ). $$
- For simplicity, the apostrophe is omitted below to denote zero mean variables.
- Both $t$ and $p$ are to be understood as zero mean up to and including the subtask (4)' .
(3) The general equation of a zero mean 2D random variable is:
- $$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 2\it \pi \cdot \sigma_{\it t}\cdot \sigma_{\it p} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 2\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it t}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{ (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it t}\cdot\sigma_{\it p}}\Bigg\}.$$
- The standard deviations $\sigma_t$ and $\sigma_p$ as well as the correlation coefficient $\rho$ can be obtained by coefficient comparison:
- A comparison of the first two terms in the exponent shows that $\sigma_t = 2 \cdot \sigma_p$ must hold. Thus the PDF is:
- $$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 4\it \pi \cdot \sigma_{\it p}^{\rm 2} \cdot\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot \hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 8\cdot (\rm 1-\rho^{\rm 2})\cdot \sigma_{\it p}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2\cdot (\rm 1-\it\rho^{\rm 2}{\rm )}\cdot \sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{\rm 2\cdot (\rm 1-\it \rho^{\rm 2}{\rm )}\cdot\sigma_{\it p}^{\rm 2}}\Bigg\}.$$
- From the second term of the exponent follows:
- $$2\cdot(1-\rho^{\rm 2})\cdot\sigma_{p}^{ 2}=0.0072\hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{p}^{2} = \frac{ 0.0036}{(1-\rho^{\rm 2})}.$$
- The factor $K = 13.263$ now gives the result.
- $$K = \frac{\sqrt{\rm 1-\it\rho^{\rm 2}}}{\rm 4\it\pi\cdot \rm 0.0036}=\rm 13.263 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sqrt{\rm 1-\it\rho^{\rm 2}}=\rm 0.6 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\hspace{0.15cm}\underline{ \rm \rho = \rm 0.8}.$$
- From this we get the standard deviations to $\sigma_t\hspace{0.15cm}\underline{= 0.2}$ and $\sigma_p\hspace{0.15cm}\underline{= 0.1}$.
- For control, we use the last term of the exponent:
- $$\frac{(1 - \rho^{2})\cdot \sigma_{\it t}\cdot\sigma_{\it p}}{\it \rho} = \frac{0.36\cdot 0.1\cdot 0.2}{0.8} = \rm 0.009.$$
- This agrees with the given value.
(4) The proposed solution 1 is correct.
- Basically, $(t, p)$ is not a true Gaussian random variable, since both components are bounded.
- The probabilities for the events $t < 0$, $t >1$, $p < 0$ and $p >1$ are therefore zero.
- However, for Gaussian variables with the mean values and standard deviations present here, we get.
- $$\rm Pr(\it t < \rm 0) = \rm Pr(\it t > \rm 1) = \rm Q(2.5)\approx 6\cdot 10^{-3},$$
- $$\rm Pr(\it p > \rm 1) = \rm Q(3)\approx 1.3\cdot 10^{-3},$$
- $$\rm Pr(\it p < \rm 0) = \rm Q(7)\approx 10^{-12}.$$
- The correlation coefficient $\rho = 0.8$ is positive here. If the examinee has done rather well in the theory part, it is to be expected (at least for this exercise) that the practical part will also go well.
- Suggestion 2 is therefore wrong here. In practice, this is certainly not always the case.
(5) For this probability, $\Delta t = \Delta p = 0.02$:
- $$\rm Pr\left [( \rm 0.5-\frac{\rm\Delta\it t}{\rm 2}\le \it t \le \rm 0.5+\frac{\rm\Delta\it t}{\rm 2})\cap(\rm 0. 5-\frac{\rm\delta\it p}{\rm 2}\le \it p \le \rm 0.5+\frac{\rm\delta\it p}{\rm 2})\right ] \approx \rm\Delta\it t\cdot\rm\Delta\it p\cdot \it f_{tp}{\rm (}t=\rm 0.5, \it p = \rm 0.5).$$
- For the 2D PDF, taking into account the mean values $m_t{= 0.5}$ and $m_p{= 0.7}$:
- $$f_{tp}(\it t=\rm 0.5, \it p=\rm 0.5) = \rm 13.263\cdot {\rm e}^{-(-0.2)^2/0.0072}\approx 0.0513.$$
- Thus, the probability we are looking for is given by
- $${\rm Pr}\big[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)\big] =0.02 \cdot 0.0513\hspace{0.15cm}\underline{\approx 2 · 10^{-5}}.$$