Difference between revisions of "Aufgaben:Exercise 4.5Z: Again Mutual Information"
m (Text replacement - "value-discrete" to "discrete") |
|||
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_Z_4_5.png|right|frame|Given joint PDF and <br>graph of differential entropies]] |
| − | + | The graph above shows the joint PDF $f_{XY}(x, y)$ to be considered in this task, which is identical to the "green" constellation in [[Aufgaben:Exercise_4.5:_Mutual_Information_from_2D-PDF|Exercise 4.5]]. | |
| − | [ | + | * In this sketch $f_{XY}(x, y)$ is enlarged by a factor of $3$ in $y$–direction. |
| + | *In the definition area highlighted in green, the joint PDF is constant equal to $C = 1/F$, where $F$ indicates the area of the parallelogram. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In Exercise 4.5 the following differential entropies were calculated: | |
| + | :$$h(X) \ = \ {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A\hspace{0.05cm})\hspace{0.05cm},$$ | ||
| + | :$$h(Y) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}B \cdot \sqrt{ {\rm e } } \hspace{0.05cm})\hspace{0.05cm},$$ | ||
| + | :$$h(XY) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}F \hspace{0.05cm}) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A \cdot B \hspace{0.05cm})\hspace{0.05cm}.$$ | ||
| + | In this exercise, the parameter values $A = {\rm e}^{-2}$ and $B = {\rm e}^{0.5}$ are now to be used. | ||
| − | + | According to the above diagram, the conditional differential entropies $h(Y|X)$ and $h(X|Y)$ should now also be determined and their relation to the mutual information $I(X; Y)$ given. | |
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN channel capacity with continuous input]]. | ||
| + | *If the results are to be given in "nat", this is achieved with "log" ⇒ "ln". | ||
| + | *If the results are to be given in "bit", this is achieved with "log" ⇒ "log<sub>2</sub>". | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | + | {State the following information theoretic quantities "nat": | |
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | $h(X)$ | + | $h(X) \ = \ $ { -2.06--1.94 } $\ \rm nat$ |
| − | $h(Y)$ | + | $h(Y) \ \hspace{0.03cm} = \ $ { 1 3% } $\ \rm nat$ |
| − | $h(XY)$ | + | $h(XY)\ \hspace{0.17cm} = \ $ { -1.55--1.45 } $\ \rm nat$ |
| − | $I(X;Y)$ | + | $I(X;Y)\ = \ $ { 0.5 3% } $\ \rm nat$ |
| − | { | + | {What are the same quantities with the pseudo–unit "bit"? |
|type="{}"} | |type="{}"} | ||
| − | $h(X)$ | + | $h(X) \ = \ $ { -2.986--2.786 } $\ \rm bit$ |
| − | $h(Y)$ | + | $h(Y) \ \hspace{0.03cm} = \ $ { 1.443 3% } $\ \rm bit$ |
| − | $h(XY)$ | + | $h(XY)\ \hspace{0.17cm} = \ $ { -2.22--2.10 } $\ \rm bit$ |
| − | $I(X;Y)$ | + | $I(X;Y)\ = \ $ { 0.721 3% } $\ \rm bit$ |
| − | { | + | {Calculate the conditional differential entropy $h(Y|X)$. |
|type="{}"} | |type="{}"} | ||
| − | $h(Y|X)$ | + | $h(Y|X) \ = \ $ { 0.5 3% } $\ \rm nat$ |
| − | $h(Y|X)$ | + | $h(Y|X) \ = \ $ { 0.721 3% } $\ \rm bit$ |
| − | { | + | {Calculate the conditional differential entropy $h(X|Y)$. |
|type="{}"} | |type="{}"} | ||
| − | $h(X|Y)$ | + | $h(X|Y) \ = \ $ { -2.6--2.4 } $\ \rm nat$ |
| − | $h(X|Y)$ | + | $h(X|Y) \ = \ $ { -3.7--3.5 } $\ \rm bit$ |
| − | { | + | {Which of the following quantities is never negative? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Both $H(X)$ and $H(Y)$ in the discrete case. |
| − | + | + | + The mutual information $I(X; Y)$ in the discrete case. |
| − | + | + | + The mutual information $I(X; Y)$ in the continuous case. |
| − | - | + | - Both $h(X)$ and $h(Y)$ in the continuous case. |
| − | - | + | - Both $h(X|Y)$ and $h(Y|X)$ in the continuous case. |
| − | - | + | - The joint entropy $h(XY)$ in the continuous case. |
| + | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Since the results are required in "nat", it is convenient to use the natural logarithm: | |
| − | + | *The random variable $X$ is uniformly distributed between $0$ and $1/{\rm e}^2={\rm e}^{-2}$: | |
| − | $$h(X) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-2}\hspace{0.05cm}) | + | :$$h(X) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-2}\hspace{0.05cm}) |
\hspace{0.15cm}\underline{= -2\,{\rm nat}}\hspace{0.05cm}. $$ | \hspace{0.15cm}\underline{= -2\,{\rm nat}}\hspace{0.05cm}. $$ | ||
| − | + | *The random variable $Y$ is triangularly distributed between $±{\rm e}^{-0.5}$: | |
| − | $$h(Y) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}\sqrt{ {\rm e} } \cdot \sqrt{ {\rm e} } ) | + | :$$h(Y) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}\sqrt{ {\rm e} } \cdot \sqrt{ {\rm e} } ) |
= {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{ { \rm e } } | = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{ { \rm e } } | ||
\hspace{0.05cm}) | \hspace{0.05cm}) | ||
\hspace{0.15cm}\underline{= +1\,{\rm nat}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= +1\,{\rm nat}}\hspace{0.05cm}.$$ | ||
| − | + | * The area of the parallelogram is given by | |
| − | $$F = A \cdot B = {\rm e}^{-2} \cdot {\rm e}^{0.5} = {\rm e}^{-1.5}\hspace{0.05cm}.$$ | + | :$$F = A \cdot B = {\rm e}^{-2} \cdot {\rm e}^{0.5} = {\rm e}^{-1.5}\hspace{0.05cm}.$$ |
| − | + | *Thus, the 2D-PDF in the area highlighted in green has constant height $C = 1/F ={\rm e}^{1.5}$ and we obtain for the joint entropy: | |
| − | $$h(XY) = {\rm ln} \hspace{0.1cm} (F) | + | :$$h(XY) = {\rm ln} \hspace{0.1cm} (F) |
= {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-1.5}\hspace{0.05cm}) | = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-1.5}\hspace{0.05cm}) | ||
\hspace{0.15cm}\underline{= -1.5\,{\rm nat}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= -1.5\,{\rm nat}}\hspace{0.05cm}.$$ | ||
| − | + | *From this we obtain for the mutual information: | |
| − | $$I(X;Y) = h(X) + h(Y) - h(XY) = -2 \,{\rm nat} + 1 \,{\rm nat} - (-1.5 \,{\rm nat} ) \hspace{0.15cm}\underline{= 0.5\,{\rm nat}}\hspace{0.05cm}.$$ | + | :$$I(X;Y) = h(X) + h(Y) - h(XY) = -2 \,{\rm nat} + 1 \,{\rm nat} - (-1.5 \,{\rm nat} ) \hspace{0.15cm}\underline{= 0.5\,{\rm nat}}\hspace{0.05cm}.$$ |
| − | + | ||
| − | $$h(X) \ = \ \frac{-2\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.886\,{\rm bit}}\hspace{0.05cm},$$ | + | |
| − | $$h(Y) \ = \ \frac{+1\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= +1.443\,{\rm bit}}\hspace{0.05cm},$$ | + | |
| − | $$h(XY) \ = \ \frac{-1.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.164\,{\rm bit}}\hspace{0.05cm},$$ | + | '''(2)''' In general, the relation $\log_2(x) = \ln(x)/\ln(2)$ holds. Thus, using the results of subtask '''(1)''', we obtain: |
| − | $$I(X;Y) \ = \ \frac{0.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ | + | :$$h(X) \ = \ \frac{-2\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.886\,{\rm bit}}\hspace{0.05cm},$$ |
| − | + | :$$h(Y) \ = \ \frac{+1\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= +1.443\,{\rm bit}}\hspace{0.05cm},$$ | |
| − | $$I(X;Y) = -2.886 \,{\rm bit} + 1.443 \,{\rm bit}+ 2.164 \,{\rm bit}{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ | + | :$$h(XY) \ = \ \frac{-1.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.164\,{\rm bit}}\hspace{0.05cm},$$ |
| − | + | :$$I(X;Y) \ = \ \frac{0.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ | |
| − | $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 1 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= 0.5\,{\rm nat}= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ | + | *Or also: |
| − | + | :$$I(X;Y) = -2.886 \,{\rm bit} + 1.443 \,{\rm bit}+ 2.164 \,{\rm bit}{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ | |
| − | $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = -2 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= -2.5\,{\rm nat}= -3.607\,{\rm bit}}\hspace{0.05cm}.$$ | + | |
| − | + | ||
| + | |||
| + | '''(3)''' The mutual information can also be written in the form $I(X;Y) = h(Y)-h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) $ : | ||
| + | :$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 1 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= 0.5\,{\rm nat}= 0.721\,{\rm bit}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' For the differential inference entropy, it holds correspondingly: | ||
| + | :$$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = -2 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= -2.5\,{\rm nat}= -3.607\,{\rm bit}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | [[File: P_ID2898__Inf_Z_4_5d.png |right|frame|Summary of all results of this exercise]] | ||
| + | *All quantities calculated here are summarized in the graph. | ||
| + | *Arrows pointing up indicate a positive contribution, arrows pointing down indicate a negative contribution. | ||
| + | |||
| + | |||
| − | + | '''(5)''' Correct are the <u>proposed solutions 1 to 3</u>. | |
| − | + | ||
| − | + | Again for clarification: | |
| − | + | * For the mutual information $I(X;Y) \ge 0$ always holds. | |
| + | * In the discrete case there is no negative entropy, but in the continuous case there is. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 106: | Line 131: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.2 AWGN and Value-Continuous Input^]] |
Latest revision as of 10:27, 11 October 2021
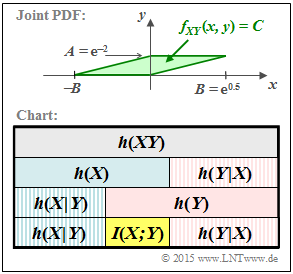
The graph above shows the joint PDF $f_{XY}(x, y)$ to be considered in this task, which is identical to the "green" constellation in Exercise 4.5.
- In this sketch $f_{XY}(x, y)$ is enlarged by a factor of $3$ in $y$–direction.
- In the definition area highlighted in green, the joint PDF is constant equal to $C = 1/F$, where $F$ indicates the area of the parallelogram.
In Exercise 4.5 the following differential entropies were calculated:
- $$h(X) \ = \ {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A\hspace{0.05cm})\hspace{0.05cm},$$
- $$h(Y) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}B \cdot \sqrt{ {\rm e } } \hspace{0.05cm})\hspace{0.05cm},$$
- $$h(XY) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}F \hspace{0.05cm}) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A \cdot B \hspace{0.05cm})\hspace{0.05cm}.$$
In this exercise, the parameter values $A = {\rm e}^{-2}$ and $B = {\rm e}^{0.5}$ are now to be used.
According to the above diagram, the conditional differential entropies $h(Y|X)$ and $h(X|Y)$ should now also be determined and their relation to the mutual information $I(X; Y)$ given.
Hints:
- The exercise belongs to the chapter AWGN channel capacity with continuous input.
- If the results are to be given in "nat", this is achieved with "log" ⇒ "ln".
- If the results are to be given in "bit", this is achieved with "log" ⇒ "log2".
Questions
Solution
- The random variable $X$ is uniformly distributed between $0$ and $1/{\rm e}^2={\rm e}^{-2}$:
- $$h(X) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-2}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -2\,{\rm nat}}\hspace{0.05cm}. $$
- The random variable $Y$ is triangularly distributed between $±{\rm e}^{-0.5}$:
- $$h(Y) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}\sqrt{ {\rm e} } \cdot \sqrt{ {\rm e} } ) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{ { \rm e } } \hspace{0.05cm}) \hspace{0.15cm}\underline{= +1\,{\rm nat}}\hspace{0.05cm}.$$
- The area of the parallelogram is given by
- $$F = A \cdot B = {\rm e}^{-2} \cdot {\rm e}^{0.5} = {\rm e}^{-1.5}\hspace{0.05cm}.$$
- Thus, the 2D-PDF in the area highlighted in green has constant height $C = 1/F ={\rm e}^{1.5}$ and we obtain for the joint entropy:
- $$h(XY) = {\rm ln} \hspace{0.1cm} (F) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-1.5}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -1.5\,{\rm nat}}\hspace{0.05cm}.$$
- From this we obtain for the mutual information:
- $$I(X;Y) = h(X) + h(Y) - h(XY) = -2 \,{\rm nat} + 1 \,{\rm nat} - (-1.5 \,{\rm nat} ) \hspace{0.15cm}\underline{= 0.5\,{\rm nat}}\hspace{0.05cm}.$$
(2) In general, the relation $\log_2(x) = \ln(x)/\ln(2)$ holds. Thus, using the results of subtask (1), we obtain:
- $$h(X) \ = \ \frac{-2\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.886\,{\rm bit}}\hspace{0.05cm},$$
- $$h(Y) \ = \ \frac{+1\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= +1.443\,{\rm bit}}\hspace{0.05cm},$$
- $$h(XY) \ = \ \frac{-1.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.164\,{\rm bit}}\hspace{0.05cm},$$
- $$I(X;Y) \ = \ \frac{0.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
- Or also:
- $$I(X;Y) = -2.886 \,{\rm bit} + 1.443 \,{\rm bit}+ 2.164 \,{\rm bit}{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
(3) The mutual information can also be written in the form $I(X;Y) = h(Y)-h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) $ :
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 1 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= 0.5\,{\rm nat}= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
(4) For the differential inference entropy, it holds correspondingly:
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = -2 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= -2.5\,{\rm nat}= -3.607\,{\rm bit}}\hspace{0.05cm}.$$
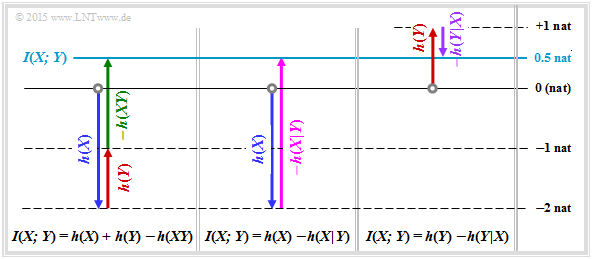
- All quantities calculated here are summarized in the graph.
- Arrows pointing up indicate a positive contribution, arrows pointing down indicate a negative contribution.
(5) Correct are the proposed solutions 1 to 3.
Again for clarification:
- For the mutual information $I(X;Y) \ge 0$ always holds.
- In the discrete case there is no negative entropy, but in the continuous case there is.