Difference between revisions of "Aufgaben:Exercise 4.6: Coordinate Rotation"
From LNTwww
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables |
}} | }} | ||
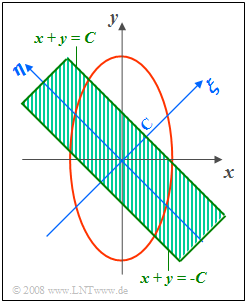
| − | [[File:P_ID431__Sto_A_4_6_neu.png|right|frame| | + | [[File:P_ID431__Sto_A_4_6_neu.png|right|frame|Coordinate rotation of a joint PDF]] |
| − | + | In the exercise we consider a two-dimensional Gaussian random variable $(x, y)$ with statistically independent components Let the standard deviations of the two components be $\sigma_x = 1$ and $\sigma_y = 2$. | |
| − | + | We want to calculate the probability that the two-dimensional random variable $(x, y)$ lies within the shaded area: | |
:$$-C \le x + y \le +C.$$ | :$$-C \le x + y \le +C.$$ | ||
| − | + | Perform a coordinate transformation to solve: | |
:$$\xi = \hspace{0.4cm} x +y,$$ | :$$\xi = \hspace{0.4cm} x +y,$$ | ||
:$$\eta= -x +y .$$ | :$$\eta= -x +y .$$ | ||
| − | + | This corresponds to a rotation of the coordinate system by $45^\circ$. | |
| − | * | + | *From $x+y= \pm C$ it thus follows $\xi=\pm C$. |
| − | * | + | *The two two-dimensional density functions are then: |
:$$f_{xy} (x,y) = \frac{1}{4 \pi} \cdot \exp \left [ - ( x^2\hspace {-0.1cm} /2 + y^2\hspace {-0.1cm} /8) \right ] ,$$ | :$$f_{xy} (x,y) = \frac{1}{4 \pi} \cdot \exp \left [ - ( x^2\hspace {-0.1cm} /2 + y^2\hspace {-0.1cm} /8) \right ] ,$$ | ||
| − | :$$f_{\xi\eta} (\xi, \eta) = \frac{1}{2 \pi \cdot \sigma_\xi \cdot \sigma_\eta \cdot \sqrt{1 - \rho_{\xi\eta}^2}} \cdot \exp \left [ - \frac{1}{2 \cdot (1 - \rho_{\xi\eta}^2)} \cdot ( \frac {\xi^2}{\sigma_\xi^2} + | + | :$$f_{\xi\eta} (\xi, \eta) = \frac{1}{2 \pi \cdot \sigma_\xi \cdot \sigma_\eta \cdot \sqrt{1 - \rho_{\xi\eta}^2}} \cdot \exp \left [ - \frac{1}{2 \cdot (1 - \rho_{\xi\eta}^2)} \cdot ( \frac {\xi^2}{\sigma_\xi^2} + \frac {\eta^2}{\sigma_\eta^2 }- 2 \rho_{\xi\eta}\cdot \frac {\xi \cdot \eta}{\sigma_\xi \cdot \sigma_\eta}) \right ] .$$ |
| Line 26: | Line 26: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables|Two-dimensional Gaussian Random Variables]]. |
| − | * | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables#Rotation_of_the_coordinate_system|Rotation of the coordinate system]]. |
| − | * | + | *Given are the approximations ${\rm Q}(2.3) \approx 0.01$ and ${\rm Q}(2.6) \approx 0.005$ for the complementary Gaussian error integral. |
| − | * | + | *More information on this topic is provided in the learning video [[Gaußsche_2D-Zufallsgrößen_(Lernvideo)|Gaussian 2D random variables]]: |
| − | :: | + | ::Part 1: Gaussian random variables without statistical bindings, |
| − | :: | + | ::Part 2: Gaussian random variables with statistical bindings. |
| Line 39: | Line 39: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the ratio of the two standard deviations of the new random variables by comparing coefficients $(\xi, \eta)$. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_\xi/\sigma_\eta \ = \ $ | + | $\sigma_\xi/\sigma_\eta \ = \ $ { 1 3% } |
| − | { | + | {Calculate the standard deviation $\sigma_\xi$ and correlation coefficient $\rho_{\xi\eta}$ between the new random variables $\xi$ and $\eta$. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_\xi \ = | + | $\sigma_\xi \ = \ $ { 2.236 3% } |
| − | $\rho_{\xi\eta} \ = | + | $\rho_{\xi\eta} \ = \ $ { 0.6 3% } |
| − | { | + | {Calculate the probability that $ |\hspace{0.05cm}x+y\hspace{0.05cm}| \le C$ holds. How large should $C$ be chosen so that $99\%$ of all sizes are in the shaded area? |
|type="{}"} | |type="{}"} | ||
| − | $C_{99\%} \ = | + | $C_{99\%} \ = \ $ { 5.814 3% } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' From $\xi = x + y$ and $\eta = -x + y$ it follows directly: |
| − | :$$x = {1}/{2} \cdot | + | :$$x = {1}/{2} \cdot ( \xi - \eta ) ,\hspace{0.5cm}y = {1}/{2}\cdot ( \xi +\eta ) .$$ |
| − | * | + | *Substituting these values for the negative exponent, we get: |
| − | :$$\frac{x^2}{2} | + | :$$\frac{x^2}{2} + \frac{y^2}{8} = \frac{1}{8} \cdot ( \xi - \eta )^2 + \frac{1}{32} \cdot ( \xi + \eta )^2.$$ |
| − | * | + | *Multiplied out, this gives: |
| − | :$$\frac{5}{32} \cdot | + | :$$\frac{5}{32} \cdot \xi^2 + \frac{5}{32} \cdot \eta^2 - \frac{3}{16} \cdot \xi \cdot \eta .$$ |
| − | * | + | *Since the coefficients on $\xi^2$ and $\eta^2$ are equal, then $\sigma_\xi = \sigma_\eta$. <u>The quotient we are looking for is therefore 1</u>. |
| − | '''(2)''' | + | '''(2)''' By comparing coefficients, we obtain for $\sigma_\xi = \sigma_\eta$ the system of equations: |
| − | :$$2 \cdot \sigma_\xi^2 \cdot | + | :$$2 \cdot \sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)= \frac{32}{5},$$ |
| − | :$$\frac{\sigma_\xi^2 \cdot | + | :$$\frac{\sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)}{\rho_{\xi\eta}}= \frac{16}{3}.$$ |
| − | * | + | *Substituting the first equation into the second, we get $\rho_{\xi\eta}\hspace{0.15cm}\underline {= 0.6}$ and $\sigma_{\xi} = \sqrt{5}\hspace{0.15cm}\underline {= 2.236}$. |
| − | '''(3)''' | + | '''(3)''' After coordinate transformation, we can write für this probability: |
| − | :$${\rm Pr} ( | x + y | \le C ) = {\rm Pr} ( | \xi | \le C ) = 1 - 2 \cdot {\rm Pr} ( | + | :$${\rm Pr} ( | x + y | \le C ) = {\rm Pr} ( | \xi | \le C ) = 1 - 2 \cdot {\rm Pr} ( \xi >C ).$$ |
| − | * | + | *With the complementary Gaussian error integral, it further follows: |
| − | :$${\rm Pr} ( | x + y | \le C ) = 1 - 2 \cdot {\rm Q} ( | + | :$${\rm Pr} ( | x + y | \le C ) = 1 - 2 \cdot {\rm Q} ( {C}/{\sigma_\xi}) = 0.99 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q} ( {C}/{\sigma_\xi}) = 0.005.$$ |
| − | * | + | *With the given value ${\rm Q}(2.6) \approx 0.005$ we thus obtain the result: |
:$$C \approx 2.6 \cdot \sigma_{\xi}\hspace{0.15cm}\underline {= 5.814}.$$ | :$$C \approx 2.6 \cdot \sigma_{\xi}\hspace{0.15cm}\underline {= 5.814}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 23:24, 25 January 2022
In the exercise we consider a two-dimensional Gaussian random variable $(x, y)$ with statistically independent components Let the standard deviations of the two components be $\sigma_x = 1$ and $\sigma_y = 2$.
We want to calculate the probability that the two-dimensional random variable $(x, y)$ lies within the shaded area:
- $$-C \le x + y \le +C.$$
Perform a coordinate transformation to solve:
- $$\xi = \hspace{0.4cm} x +y,$$
- $$\eta= -x +y .$$
This corresponds to a rotation of the coordinate system by $45^\circ$.
- From $x+y= \pm C$ it thus follows $\xi=\pm C$.
- The two two-dimensional density functions are then:
- $$f_{xy} (x,y) = \frac{1}{4 \pi} \cdot \exp \left [ - ( x^2\hspace {-0.1cm} /2 + y^2\hspace {-0.1cm} /8) \right ] ,$$
- $$f_{\xi\eta} (\xi, \eta) = \frac{1}{2 \pi \cdot \sigma_\xi \cdot \sigma_\eta \cdot \sqrt{1 - \rho_{\xi\eta}^2}} \cdot \exp \left [ - \frac{1}{2 \cdot (1 - \rho_{\xi\eta}^2)} \cdot ( \frac {\xi^2}{\sigma_\xi^2} + \frac {\eta^2}{\sigma_\eta^2 }- 2 \rho_{\xi\eta}\cdot \frac {\xi \cdot \eta}{\sigma_\xi \cdot \sigma_\eta}) \right ] .$$
Hints:
- The exercise belongs to the chapter Two-dimensional Gaussian Random Variables.
- Reference is also made to the chapter Rotation of the coordinate system.
- Given are the approximations ${\rm Q}(2.3) \approx 0.01$ and ${\rm Q}(2.6) \approx 0.005$ for the complementary Gaussian error integral.
- More information on this topic is provided in the learning video Gaussian 2D random variables:
- Part 1: Gaussian random variables without statistical bindings,
- Part 2: Gaussian random variables with statistical bindings.
Questions
Solution
(1) From $\xi = x + y$ and $\eta = -x + y$ it follows directly:
- $$x = {1}/{2} \cdot ( \xi - \eta ) ,\hspace{0.5cm}y = {1}/{2}\cdot ( \xi +\eta ) .$$
- Substituting these values for the negative exponent, we get:
- $$\frac{x^2}{2} + \frac{y^2}{8} = \frac{1}{8} \cdot ( \xi - \eta )^2 + \frac{1}{32} \cdot ( \xi + \eta )^2.$$
- Multiplied out, this gives:
- $$\frac{5}{32} \cdot \xi^2 + \frac{5}{32} \cdot \eta^2 - \frac{3}{16} \cdot \xi \cdot \eta .$$
- Since the coefficients on $\xi^2$ and $\eta^2$ are equal, then $\sigma_\xi = \sigma_\eta$. The quotient we are looking for is therefore 1.
(2) By comparing coefficients, we obtain for $\sigma_\xi = \sigma_\eta$ the system of equations:
- $$2 \cdot \sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)= \frac{32}{5},$$
- $$\frac{\sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)}{\rho_{\xi\eta}}= \frac{16}{3}.$$
- Substituting the first equation into the second, we get $\rho_{\xi\eta}\hspace{0.15cm}\underline {= 0.6}$ and $\sigma_{\xi} = \sqrt{5}\hspace{0.15cm}\underline {= 2.236}$.
(3) After coordinate transformation, we can write für this probability:
- $${\rm Pr} ( | x + y | \le C ) = {\rm Pr} ( | \xi | \le C ) = 1 - 2 \cdot {\rm Pr} ( \xi >C ).$$
- With the complementary Gaussian error integral, it further follows:
- $${\rm Pr} ( | x + y | \le C ) = 1 - 2 \cdot {\rm Q} ( {C}/{\sigma_\xi}) = 0.99 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q} ( {C}/{\sigma_\xi}) = 0.005.$$
- With the given value ${\rm Q}(2.6) \approx 0.005$ we thus obtain the result:
- $$C \approx 2.6 \cdot \sigma_{\xi}\hspace{0.15cm}\underline {= 5.814}.$$