Difference between revisions of "Aufgaben:Exercise 4.8: Numerical Analysis of the AWGN Channel Capacity"
m (Guenter verschob die Seite 4.8 Kurvenverlauf C(EB/N0) nach 4.8 Numerische Auswertung der AWGN-Kanalkapazität) |
|||
| (32 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Discrete_Input |
}} | }} | ||
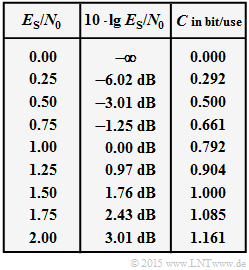
| − | [[File:P_ID2936__Inf_A_4_8_Tab.png|right|]] | + | [[File:P_ID2936__Inf_A_4_8_Tab.png|right|frame|$C$ as a function of $E_{\rm S}/{N_0}$]] |
| − | + | There are two different equations for the channel capacity $C$ of the AWGN channel as an upper bound for the code rate $R$ in digital signal transmission: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | $\text{Channel capacity as a function of energy per symbol}$: | |
| − | $$C( E_{\rm | + | :$$C( E_{\rm S}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S}}{N_0}) .$$ |
| + | Here, the following abbreviations are used: | ||
| + | * $E_{\rm S}$ denotes the (average) energy per symbol of the digital signal, | ||
| + | * $N_0$ indicates the AWGN noise power density. | ||
| − | |||
| − | |||
| + | $\text{Channel capacity as a function of energy per bit}$: | ||
| + | :$$C( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) .$$ | ||
| − | + | *The relation $E_{\rm S} = R \cdot E_{\rm B}$ has to be considered, where $R$ is the code rate of the best possible channel coding. | |
| − | + | *Error-free transmission (with optimal code) is possible for the given $E_{\rm B}/N_0$ as long as $R \le C$ ⇒ [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Definition_and_meaning_of_channel_capacity|Shannon's channel coding theorem ]] holds. | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | + | Given by the table is the curve of channel capacity as a function of $E_{\rm S}/N_0$. The focus of this exercise is the numerical evaluation of the second equation. | |
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/AWGN_Channel_Capacity_for_Discrete_Input|AWGN channel capacity for discrete value input]]. | ||
| + | *Reference is made in particular to the pages | ||
| + | **[[Information_Theory/AWGN_Channel_Capacity_for_Discrete_Input#The_channel_capacity_.7F.27.22.60UNIQ-MathJax81-QINU.60.22.27.7F_as_a_function_of_.7F.27.22.60UNIQ-MathJax82-QINU.60.22.27.7F|The channel capacity $C$ as a function of $E_{\rm S}/{N_0}$]], | ||
| + | **[[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#The_channel_capacity_.7F.27.22.60UNIQ-MathJax128-QINU.60.22.27.7F_as_a_function_of_.7F.27.22.60UNIQ-MathJax129-QINU.60.22.27.7F|The channel capacity $C$ as a function of $E_{\rm B}/{N_0}$]]. | ||
| + | *Since the results are to be expressed in "bit", "log" ⇒ "log<sub>2</sub>" is used in the equations. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which equations accurately describe the relationship between $E_{\rm B}/{N_0}$ and the rate $R$ for the AWGN channel? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $R = 1/2 \cdot \log_2 (1 + 2 \cdot R \cdot E_{\rm B}/{N_0})$. |
| − | + 2 | + | + $2^{2R} = 1 + 2 \cdot R \cdot E_{\rm B}/{N_0}$. |
| − | + | + | + $E_{\rm B}/{N_0} = (2^{2R} -1)/(2R) $. |
| − | { | + | {Specify the smallest possible value for $E_{\rm B}/{N_0}$ that can still be used to transmit over the AWGN channel without errors. |
|type="{}"} | |type="{}"} | ||
| − | $Min [ | + | $\text{Min} \ \big[E_{\rm B}/{N_0}\big] \ = \ $ { 0.693 3% } |
| − | { | + | {Which result is obtained in $\rm dB$? |
|type="{}"} | |type="{}"} | ||
| − | $Min[10 | + | $\text{Min} \ \big[10 \cdot \lg (E_{\rm B}/{N_0})\big] \ = \ $ { -1.62--0.156 } $ \ \rm dB$ |
| − | { | + | {Give the AWGN channel capacity $C$ for $10 \cdot \lg (E_{\rm B}/{N_0}) = 0$ dB. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $C \ = \ $ { 0.5 3% } $ \ \rm bit/channel\:use$ |
| − | |||
| − | { | + | {Specify the required $E_{\rm B}/{N_0}$ for error-free transmission with $R = 1$ . <br>Note: The solution can be found in the table on the information page. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\text{Min} \ \big[E_{\rm B}/{N_0}\big] \ = \ $ { 1.5 3% } |
| − | { | + | {How can a point of the $C(E_{\rm B}/{N_0})$ curve be determined more easily? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Calculation of the channel capacity $C$ for the given $E_{\rm B}/{N_0}$. |
| − | + | + | + Calculation of the required $E_{\rm B}/{N_0}$ for the given $C$. |
| Line 69: | Line 77: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>All proposed solutions</u> are correct: |
| − | $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot E_{\rm S}}/{N_0}) $$ | + | *Based on the equation |
| − | + | :$$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot E_{\rm S}}/{N_0}) $$ | |
| − | $$R = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot R \cdot E_{\rm B}}/{N_0})\hspace{0.05cm}. $$ | + | :we obtain with $C = R$ and $E_{\rm S} = R · E_{\rm B}$ the equation according to solution suggestion 1: |
| − | + | :$$R = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot R \cdot E_{\rm B}}/{N_0})\hspace{0.05cm}. $$ | |
| − | $$2^{2R} = 1 + 2 \cdot R \cdot E_{\rm B}/{N_0}\hspace{0.05cm}. $$ | + | *Bringing the factor $1/2$ to the left side of the equation and forming the power to the base $2$, we get the suggestion 2: |
| − | + | :$$2^{2R} = 1 + 2 \cdot R \cdot E_{\rm B}/{N_0}\hspace{0.05cm}. $$ | |
| − | $$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$ | + | *If we solve this equation for $E_{\rm B}/{N_0}$, we get |
| − | + | :$$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$ | |
| − | |||
| − | + | ||
| − | $${\rm Min}\hspace{0.1cm}[E_{\rm B}/{N_0}] = \lim\limits_{R \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$ | + | '''(2)''' Error-free transmission is possible over a channel with channel capacity $C$ as long as the code rate is $R ≤ C$. |
| − | + | *The absolute limit is obtained in the limiting case $C=R = 0$. | |
| − | $${\rm Min}\hspace{0.1cm}[E_{\rm B}/{N_0}] = \lim\limits_{x \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{x} - 1} { x} = \frac{{\rm ln}\hspace{0.1cm} (2) \cdot 2^{x} } { 1} \hspace{0.05cm}\bigg |_{x=0} | + | |
| + | *Or more precisely: For an arbitrarily small positive $ε$, the following must hold: $C=R =ε$ with $ε → 0$. | ||
| + | |||
| + | *Using the result of subtask '''(1)''', the governing equation is: | ||
| + | :$${\rm Min}\hspace{0.1cm}\big[E_{\rm B}/{N_0}\big] = \lim\limits_{R \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$ | ||
| + | *Since here the quotient in the boundary transition $ R → 0$ yields the result "0 divided by 0", the [https://https://en.wikipedia.org/wiki/L%27H%C3%B4pital%27s_rule l'Hospital's rule] is to be applied here: <br>Differentiate numerator and denominator, form the quotient and finally put $R = 0$ . | ||
| + | *With $x = 2R$ the result is: | ||
| + | :$${\rm Min}\hspace{0.1cm}\big[E_{\rm B}/{N_0}\big] = \lim\limits_{x \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{x} - 1} { x} = \frac{{\rm ln}\hspace{0.1cm} (2) \cdot 2^{x} } { 1} \hspace{0.05cm}\bigg |_{x=0} | ||
= {\rm ln}\hspace{0.1cm} (2) \hspace{0.15cm}\underline{= 0.693} | = {\rm ln}\hspace{0.1cm} (2) \hspace{0.15cm}\underline{= 0.693} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(3)''' In | + | |
| − | $${\rm Min}\hspace{0.1cm}[10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})] = | + | |
| + | '''(3)''' In logarithmic form, we obtain:: | ||
| + | :$${\rm Min}\hspace{0.1cm}\big[10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})\big] = | ||
10\cdot {\rm lg} \hspace{0.1cm}(0.693) \hspace{0.15cm}\underline{= -1.59\,{\rm dB}} | 10\cdot {\rm lg} \hspace{0.1cm}(0.693) \hspace{0.15cm}\underline{= -1.59\,{\rm dB}} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | '''(4)''' | + | |
| − | $$\frac{2^{2C} - 1} { 2 C} \stackrel{!}{=} 1 | + | |
| + | '''(4)''' Thus, the abscissa value in non-logarithmic form is: $E_{\rm B}/{N_0} = 1$. It follows with $C=R$: | ||
| + | :$$\frac{2^{2C} - 1} { 2 C} \stackrel{!}{=} 1 | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{C = 0.5} | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{C = 0.5} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | '''(5)''' | + | |
| − | $$ C(E_{\rm B}/{N_0}) = 1 \hspace{0.3cm}\Longleftrightarrow \hspace{0.3cm} | + | |
| + | '''(5)''' For $R = 1$ ⇒ $E_{\rm B} = E_{\rm S}$. Therefore: | ||
| + | :$$ C(E_{\rm B}/{N_0}) = 1 \hspace{0.3cm}\Longleftrightarrow \hspace{0.3cm} | ||
C(E_{\rm S}/{N_0}) = 1 | C(E_{\rm S}/{N_0}) = 1 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *From the table on the information page we can read: | |
| − | $$ C(E_{\rm S}/{N_0}) = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | + | :$$ C(E_{\rm S}/{N_0}) = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |
E_{\rm S}/{N_0} = 1.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | E_{\rm S}/{N_0} = 1.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
\underline{E_{\rm B}/{N_0} = 1.5}\hspace{0.05cm}.$$ | \underline{E_{\rm B}/{N_0} = 1.5}\hspace{0.05cm}.$$ | ||
| − | + | *The corresponding dB value is $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76 \ \rm dB$. | |
| − | + | *The same result is obtained with $R = 1$ via the equation | |
| − | $$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 \cdot R} | + | :$$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 \cdot R} |
= \frac{4 - 1} { 2 } = 1.5 \hspace{0.05cm}.$$ | = \frac{4 - 1} { 2 } = 1.5 \hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | |
| − | + | ||
| − | $$31.62 = \frac{2^{x} - 1} { x} | + | |
| + | '''(6)''' <u>Proposed solution 2 2</u>, is correct, as will be shown by an example: | ||
| + | |||
| + | '''(a)''' The channel capacity $C$ for $10 \cdot \lg (E_{\rm B}/{N_0}) = 15 \ \rm dB$ ⇒ $\E_{\rm B}/{N_0} = 31.62$ is sought. | ||
| + | [[File:EN_Inf_A_4_8_neu.png|right|frame|Capacity curves as a function of $10 \cdot \lg (E_{\rm S}/{N_0})$ and $10 \cdot \lg (E_{\rm B}/{N_0})$]] | ||
| + | *Then, according to the proposed solution 1 with $x = 2C$: | ||
| + | :$$31.62 = \frac{2^{x} - 1} { x} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
31.62 \cdot x = 2^{x} - 1 | 31.62 \cdot x = 2^{x} - 1 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | *The solution $x = 7.986$ ⇒ $C = 3.993 \ \rm (bit/use)$ can only be found graphically or iteratively. | |
| + | |||
| − | + | '''(b)''' The necessary abscissa value $10 \cdot \lg (E_{\rm B}/{N_0})$ for the capacity $C = 4 \ \rm bit/symbol$ is sought: | |
| − | $$E_{\rm B}/{N_0} = \frac{2^{2C} - 1} { 2 \cdot C} | + | :$$E_{\rm B}/{N_0} = \frac{2^{2C} - 1} { 2 \cdot C} |
| − | = \frac{2^8 - 1} { 8 } = 31.875 | + | = \frac{2^8 - 1} { 8 } = 31.875$$ |
| − | + | :$$\Rightarrow \hspace{0.3cm} | |
10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0}) = 15.03\,{\rm dB} | 10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0}) = 15.03\,{\rm dB} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | + | The graph shows the AWGN channel capacity as a function of | |
| − | + | * $10 \cdot \lg (E_{\rm S}/{N_0})$ ⇒ red curve and numbers; <br>these indicate the channel capacity $C$ for the given $10 \cdot \lg (E_{\rm S}/{N_0})$ ; | |
| + | * $10 \cdot \lg (E_{\rm B}/{N_0})$ ⇒ green curve and numbers; <br>these indicate the required $10 \cdot \lg (E_{\rm B}/{N_0})$ for the given channel capacity $C$ . | ||
| + | |||
| + | |||
| + | The intersection of the two curves is at $1.76\ \rm dB$. | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.3 AWGN and Value-Discrete Input^]] |
Latest revision as of 10:58, 4 November 2021
There are two different equations for the channel capacity $C$ of the AWGN channel as an upper bound for the code rate $R$ in digital signal transmission:
$\text{Channel capacity as a function of energy per symbol}$:
- $$C( E_{\rm S}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S}}{N_0}) .$$
Here, the following abbreviations are used:
- $E_{\rm S}$ denotes the (average) energy per symbol of the digital signal,
- $N_0$ indicates the AWGN noise power density.
$\text{Channel capacity as a function of energy per bit}$:
- $$C( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) .$$
- The relation $E_{\rm S} = R \cdot E_{\rm B}$ has to be considered, where $R$ is the code rate of the best possible channel coding.
- Error-free transmission (with optimal code) is possible for the given $E_{\rm B}/N_0$ as long as $R \le C$ ⇒ Shannon's channel coding theorem holds.
Given by the table is the curve of channel capacity as a function of $E_{\rm S}/N_0$. The focus of this exercise is the numerical evaluation of the second equation.
Hints:
- The exercise belongs to the chapter AWGN channel capacity for discrete value input.
- Reference is made in particular to the pages
- Since the results are to be expressed in "bit", "log" ⇒ "log2" is used in the equations.
Questions
Solution
- Based on the equation
- $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot E_{\rm S}}/{N_0}) $$
- we obtain with $C = R$ and $E_{\rm S} = R · E_{\rm B}$ the equation according to solution suggestion 1:
- $$R = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot R \cdot E_{\rm B}}/{N_0})\hspace{0.05cm}. $$
- Bringing the factor $1/2$ to the left side of the equation and forming the power to the base $2$, we get the suggestion 2:
- $$2^{2R} = 1 + 2 \cdot R \cdot E_{\rm B}/{N_0}\hspace{0.05cm}. $$
- If we solve this equation for $E_{\rm B}/{N_0}$, we get
- $$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$
(2) Error-free transmission is possible over a channel with channel capacity $C$ as long as the code rate is $R ≤ C$.
- The absolute limit is obtained in the limiting case $C=R = 0$.
- Or more precisely: For an arbitrarily small positive $ε$, the following must hold: $C=R =ε$ with $ε → 0$.
- Using the result of subtask (1), the governing equation is:
- $${\rm Min}\hspace{0.1cm}\big[E_{\rm B}/{N_0}\big] = \lim\limits_{R \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$
- Since here the quotient in the boundary transition $ R → 0$ yields the result "0 divided by 0", the l'Hospital's rule is to be applied here:
Differentiate numerator and denominator, form the quotient and finally put $R = 0$ . - With $x = 2R$ the result is:
- $${\rm Min}\hspace{0.1cm}\big[E_{\rm B}/{N_0}\big] = \lim\limits_{x \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{x} - 1} { x} = \frac{{\rm ln}\hspace{0.1cm} (2) \cdot 2^{x} } { 1} \hspace{0.05cm}\bigg |_{x=0} = {\rm ln}\hspace{0.1cm} (2) \hspace{0.15cm}\underline{= 0.693} \hspace{0.05cm}.$$
(3) In logarithmic form, we obtain::
- $${\rm Min}\hspace{0.1cm}\big[10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})\big] = 10\cdot {\rm lg} \hspace{0.1cm}(0.693) \hspace{0.15cm}\underline{= -1.59\,{\rm dB}} \hspace{0.05cm}. $$
(4) Thus, the abscissa value in non-logarithmic form is: $E_{\rm B}/{N_0} = 1$. It follows with $C=R$:
- $$\frac{2^{2C} - 1} { 2 C} \stackrel{!}{=} 1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{C = 0.5} \hspace{0.05cm}. $$
(5) For $R = 1$ ⇒ $E_{\rm B} = E_{\rm S}$. Therefore:
- $$ C(E_{\rm B}/{N_0}) = 1 \hspace{0.3cm}\Longleftrightarrow \hspace{0.3cm} C(E_{\rm S}/{N_0}) = 1 \hspace{0.05cm}.$$
- From the table on the information page we can read:
- $$ C(E_{\rm S}/{N_0}) = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} E_{\rm S}/{N_0} = 1.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{E_{\rm B}/{N_0} = 1.5}\hspace{0.05cm}.$$
- The corresponding dB value is $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76 \ \rm dB$.
- The same result is obtained with $R = 1$ via the equation
- $$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 \cdot R} = \frac{4 - 1} { 2 } = 1.5 \hspace{0.05cm}.$$
(6) Proposed solution 2 2, is correct, as will be shown by an example:
(a) The channel capacity $C$ for $10 \cdot \lg (E_{\rm B}/{N_0}) = 15 \ \rm dB$ ⇒ $\E_{\rm B}/{N_0} = 31.62$ is sought.
- Then, according to the proposed solution 1 with $x = 2C$:
- $$31.62 = \frac{2^{x} - 1} { x} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 31.62 \cdot x = 2^{x} - 1 \hspace{0.05cm}. $$
- The solution $x = 7.986$ ⇒ $C = 3.993 \ \rm (bit/use)$ can only be found graphically or iteratively.
(b) The necessary abscissa value $10 \cdot \lg (E_{\rm B}/{N_0})$ for the capacity $C = 4 \ \rm bit/symbol$ is sought:
- $$E_{\rm B}/{N_0} = \frac{2^{2C} - 1} { 2 \cdot C} = \frac{2^8 - 1} { 8 } = 31.875$$
- $$\Rightarrow \hspace{0.3cm} 10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0}) = 15.03\,{\rm dB} \hspace{0.05cm}.$$
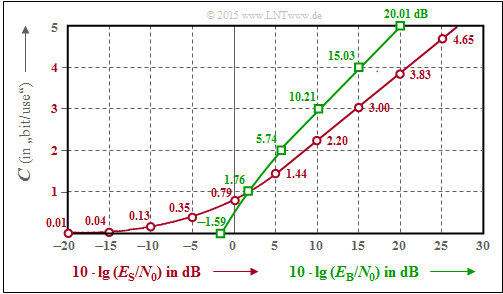
The graph shows the AWGN channel capacity as a function of
- $10 \cdot \lg (E_{\rm S}/{N_0})$ ⇒ red curve and numbers;
these indicate the channel capacity $C$ for the given $10 \cdot \lg (E_{\rm S}/{N_0})$ ; - $10 \cdot \lg (E_{\rm B}/{N_0})$ ⇒ green curve and numbers;
these indicate the required $10 \cdot \lg (E_{\rm B}/{N_0})$ for the given channel capacity $C$ .
The intersection of the two curves is at $1.76\ \rm dB$.