Difference between revisions of "Aufgaben:Exercise 4.8Z: What does the AWGN Channel Capacity Curve say?"
From LNTwww
| Line 8: | Line 8: | ||
* The curve is shown on the right with logarithmic abscissa between $-2 \ \rm dB$ and $+6 \ \rm dB$ dargestellt. | * The curve is shown on the right with logarithmic abscissa between $-2 \ \rm dB$ and $+6 \ \rm dB$ dargestellt. | ||
* The addition of "Gaussian" indicates that a Gaussian distribution was assumed for this curve at the AWGN input. | * The addition of "Gaussian" indicates that a Gaussian distribution was assumed for this curve at the AWGN input. | ||
| + | |||
Three system variants are indicated by dots in the graph: | Three system variants are indicated by dots in the graph: | ||
| Line 65: | Line 66: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u>Proposed solutions 1 and 3</u> are correct: | + | '''(1)''' <u>Proposed solutions 1 and 3</u> are correct: |
| − | *Since the point $X$ lies to the right of the channel capacity curve $C_\text{ | + | *Since the point $X$ lies to the right of the channel capacity curve $C_\text{Gaussian}(E_{\rm B}/{N_0})$, there is (at least) one transmission system of rate $R = 1$ that provides "quasi–error–free" transmission with $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$. |
| − | *Despite the code rate $R = 1$ | + | *Despite the code rate $R = 1$, this system includes a channel coding with an infinitely long code, but unfortunately this code is unknown. |
| − | *However, a binary system of rate $R = 1$ does not allow channel coding. | + | *However, a binary system of rate $R = 1$ does not allow channel coding. |
| − | '''(2)''' Only the <u>proposed solution 2</u> is correct. Here the following statements are valid: | + | '''(2)''' Only the <u>proposed solution 2</u> is correct. Here the following statements are valid: |
* The required $E_{\rm B}/{N_0}$ for the rate $R = 2$ results in | * The required $E_{\rm B}/{N_0}$ for the rate $R = 2$ results in | ||
:$$(E_{\rm B}/{N_0})_{\rm min} = \frac{2^{2R} - 1} { 2 \cdot R} | :$$(E_{\rm B}/{N_0})_{\rm min} = \frac{2^{2R} - 1} { 2 \cdot R} | ||
| Line 89: | Line 90: | ||
| − | '''(3)''' With a binary system, the rate $R = 1.5$ can never be realized ⇒ <u>proposed solution 1</u>. | + | '''(3)''' With a binary system, the rate $R = 1.5$ can never be realized ⇒ <u>proposed solution 1</u>. |
| − | '''(4)''' Correct is the <u>proposed solution 2</u>: | + | '''(4)''' Correct is the <u>proposed solution 2</u>: |
| − | *The point $Z$ | + | *The point $Z$ lies to the right of the boundary curve and for the code rate of a quaternary system holds $R \le 2$. |
| − | *So the rate $R =1.5$ would be quite realizable with $M_X = 4$ | + | *So the code rate $R =1.5$ would be quite realizable with $M_X = 4$. |
| − | *The proposed solution 1 is wrong. On the other hand, the second solution suggestion is correct: | + | *The proposed solution 1 is wrong. On the other hand,holds the second solution suggestion is correct: |
| − | * The given curve $C_\text{ | + | * The given curve $C_\text{Gaussian}(E_{\rm B}/{N_0})$ always assumes a Gaussian distributed input. |
| − | * For a binary system, a different boundary curve results, namely $C_\text{BPSK} ≤ 1 \ \rm bit/channel use$. $C_\text{ | + | * For a binary system, a different boundary curve results, namely $C_\text{BPSK} ≤ 1 \ \rm bit/channel \ use$. $C_\text{Gaussian}$ and $C_\text{BPSK}$ are significantly different. |
| − | * For the quaternary system $(M_X = 4)$ one would have to calculate and analyze the curve $C_{M=4}$ . Again, $C_{M=4} ≤ C_\text{ | + | * For the quaternary system $(M_X = 4)$ one would have to calculate and analyze the curve $C_{M=4}$ . Again, $C_{M=4} ≤ C_\text{Gaussian}$ . |
| − | *For small $E_{\rm B}/{N_0}$ | + | *For small $E_{\rm B}/{N_0}$: $C_{M=4} \approx C_\text{Gaussian}$ holds, after which the curve diverges significantly and ends in a horizontal at $C_{M=4} = 2 \ \rm bit/channel \ use$. |
The point $Z$ ⇒ $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB, \ \ R = 1.5$ lies below $C_{M=4}$. | The point $Z$ ⇒ $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB, \ \ R = 1.5$ lies below $C_{M=4}$. | ||
| − | *Such a quaternary system would thus be feasible, as will be shown in [[Aufgaben:Aufgabe_4.Zehn:_QPSK–Kanalkapazität|Exercise 4.10]] . | + | *Such a quaternary system would thus be feasible, as will be shown in [[Aufgaben:Aufgabe_4.Zehn:_QPSK–Kanalkapazität|Exercise 4.10]] . |
| − | *But only from knowledge of $C_\text{ | + | *But only from knowledge of $C_\text{Gaussian}$ the question cannot be answered (<u>proposed solution 2</u>). |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:15, 4 November 2021
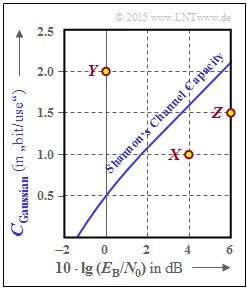
We consider the channel capacity of the AWGN channel as in Exercise 4.8:
- $$C_{\rm Gaussian}( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) . $$
- The curve is shown on the right with logarithmic abscissa between $-2 \ \rm dB$ and $+6 \ \rm dB$ dargestellt.
- The addition of "Gaussian" indicates that a Gaussian distribution was assumed for this curve at the AWGN input.
Three system variants are indicated by dots in the graph:
- System $X$: with $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$ and $R = 1$,
- System $Y$: with $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ and $R = 2$,
- System $Z$: with $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB$ and $R = 1.5$.
In the questions for this exercise, we still use the following terms:
- Digital system: Symbol set size $M_X = |X|$ beliebig,
- Binary system: Symbol set size $M_X = 2$,
- Quaternary system: Symbol set size $M_X = 4$.
Hints:
- The exercise belongs to the chapter AWGN channel capacity with discrete value input.
- Reference is made in particular to the page The channel capacity $C$ as a function of $E_{\rm B}/{N_0}$.
- Since the results are to be given in "bit" ⇒ "log" ⇒ "log2" is used in the equations.
Questions
Solution
(1) Proposed solutions 1 and 3 are correct:
- Since the point $X$ lies to the right of the channel capacity curve $C_\text{Gaussian}(E_{\rm B}/{N_0})$, there is (at least) one transmission system of rate $R = 1$ that provides "quasi–error–free" transmission with $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$.
- Despite the code rate $R = 1$, this system includes a channel coding with an infinitely long code, but unfortunately this code is unknown.
- However, a binary system of rate $R = 1$ does not allow channel coding.
(2) Only the proposed solution 2 is correct. Here the following statements are valid:
- The required $E_{\rm B}/{N_0}$ for the rate $R = 2$ results in
- $$(E_{\rm B}/{N_0})_{\rm min} = \frac{2^{2R} - 1} { 2 \cdot R} = \frac{2^4 - 1} { 4 } = 3.75 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})_{\rm min} = 15.74\,{\rm dB} \hspace{0.05cm}. $$
- The maximum code rate $R_{\rm max}$ for $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ ⇒ $E_{\rm B}/{N_0} = 1$ is calculated as follows:
- $$C = R = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2^{2R} - 1 \stackrel{!}{=} 2 R \hspace{0.3cm}\Rightarrow \hspace{0.3cm} R_{\rm max} = 0.5 \hspace{0.05cm}. $$
- Both calculations show that the point $Y$ with characteristics $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ and $R = 1$ does not satisfy the channel coding theorem.
(3) With a binary system, the rate $R = 1.5$ can never be realized ⇒ proposed solution 1.
(4) Correct is the proposed solution 2:
- The point $Z$ lies to the right of the boundary curve and for the code rate of a quaternary system holds $R \le 2$.
- So the code rate $R =1.5$ would be quite realizable with $M_X = 4$.
- The proposed solution 1 is wrong. On the other hand,holds the second solution suggestion is correct:
- The given curve $C_\text{Gaussian}(E_{\rm B}/{N_0})$ always assumes a Gaussian distributed input.
- For a binary system, a different boundary curve results, namely $C_\text{BPSK} ≤ 1 \ \rm bit/channel \ use$. $C_\text{Gaussian}$ and $C_\text{BPSK}$ are significantly different.
- For the quaternary system $(M_X = 4)$ one would have to calculate and analyze the curve $C_{M=4}$ . Again, $C_{M=4} ≤ C_\text{Gaussian}$ .
- For small $E_{\rm B}/{N_0}$: $C_{M=4} \approx C_\text{Gaussian}$ holds, after which the curve diverges significantly and ends in a horizontal at $C_{M=4} = 2 \ \rm bit/channel \ use$.
The point $Z$ ⇒ $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB, \ \ R = 1.5$ lies below $C_{M=4}$.
- Such a quaternary system would thus be feasible, as will be shown in Exercise 4.10 .
- But only from knowledge of $C_\text{Gaussian}$ the question cannot be answered (proposed solution 2).