Difference between revisions of "Aufgaben:Exercise 4.9Z: Is Channel Capacity C ≡ 1 possible with BPSK?"
| Line 25: | Line 25: | ||
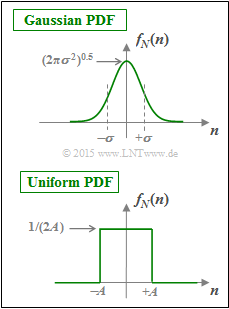
Assuming a Gaussian distribution $f_N(n)$ for the noise $N$ according to the upper sketch, we obtain the channel capacity $C_\text{BPSK} = I(X;Y)$, which is shown in the [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#AWGN_channel_capacity_for_binary_input_signals|theory section]] depending on $10 \cdot \lg (E_{\rm B}/{N_0})$ . | Assuming a Gaussian distribution $f_N(n)$ for the noise $N$ according to the upper sketch, we obtain the channel capacity $C_\text{BPSK} = I(X;Y)$, which is shown in the [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#AWGN_channel_capacity_for_binary_input_signals|theory section]] depending on $10 \cdot \lg (E_{\rm B}/{N_0})$ . | ||
| − | The question to be answered is whether there is a finite $E_{\rm B}/{N_0}$ value for which $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/channel use $ is possible ⇒ subtask '''(5)'''. | + | The question to be answered is whether there is a finite $E_{\rm B}/{N_0}$ value for which $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/channel\:use $ is possible ⇒ subtask '''(5)'''. |
In subtasks '''(1)''' to '''(4)''' , preliminary work is done to answer this question. The uniformly distributed noise PDF $f_N(n)$ is always assumed (see sketch below): | In subtasks '''(1)''' to '''(4)''' , preliminary work is done to answer this question. The uniformly distributed noise PDF $f_N(n)$ is always assumed (see sketch below): | ||
| Line 51: | Line 51: | ||
{ What is the differential interference entropy for uniformly distributed interference with $\underline{A = 1/8}$? | { What is the differential interference entropy for uniformly distributed interference with $\underline{A = 1/8}$? | ||
|type="{}"} | |type="{}"} | ||
| − | $h(N) \ = \ $ { -2.06--1.94 } $\ \rm bit/ | + | $h(N) \ = \ $ { -2.06--1.94 } $\ \rm bit/symbol$ |
{What is the differential sink entropy for uniformly distributed noise with $\underline{A = 1/8}$? | {What is the differential sink entropy for uniformly distributed noise with $\underline{A = 1/8}$? | ||
|type="{}"} | |type="{}"} | ||
| − | $h(Y) \ = \ $ { -1.03--0.97 } $\ \rm bit/ | + | $h(Y) \ = \ $ { -1.03--0.97 } $\ \rm bit/symbol$ |
| − | {What is the magnitude of the mutual information between the source and sink? Assume further a uniformly distributed noise with $\underline{A = 1/8}$ | + | {What is the magnitude of the mutual information between the source and sink? Assume further a uniformly distributed noise with $\underline{A = 1/8}$ . |
|type="{}"} | |type="{}"} | ||
| − | $I(X;Y) \ = \ $ { 1 3% } $\ \rm bit/ | + | $I(X;Y) \ = \ $ { 1 3% } $\ \rm bit/symbol$ |
| Line 71: | Line 71: | ||
{Now answer the crucial question, assuming, <br>that a Gaussian perturbation is present and the quotient $E_{\rm B}/{N_0}$ is finite. | {Now answer the crucial question, assuming, <br>that a Gaussian perturbation is present and the quotient $E_{\rm B}/{N_0}$ is finite. | ||
|type="()"} | |type="()"} | ||
| − | - $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/channel use $ is possible with a Gaussian PDF. | + | - $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/channel\:use $ is possible with a Gaussian PDF. |
| − | + For Gaussian noise with finite $E_{\rm B}/{N_0}$ , $C_\text{BPSK}(E_{\rm B}/{N_0}) < 1 \ \rm bit/channel use $ is always valid.. | + | + For Gaussian noise with finite $E_{\rm B}/{N_0}$ , $C_\text{BPSK}(E_{\rm B}/{N_0}) < 1 \ \rm bit/channel\:use $ is always valid.. |
| Line 79: | Line 79: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The differential entropy of a uniform distribution of absolute width $2A$ is equal to |
:$$ h(N) = {\rm log}_2 \hspace{0.1cm} (2A) | :$$ h(N) = {\rm log}_2 \hspace{0.1cm} (2A) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | ||
\hspace{0.15cm}h(N) = {\rm log}_2 \hspace{0.1cm} (1/4) | \hspace{0.15cm}h(N) = {\rm log}_2 \hspace{0.1cm} (1/4) | ||
| − | \hspace{0.15cm}\underline{= -2\,{\rm bit(/ | + | \hspace{0.15cm}\underline{= -2\,{\rm bit(/symbol)}}\hspace{0.05cm}.$$ |
| − | [[File:EN_Inf_Z_4_9b.png|right|frame| | + | [[File:EN_Inf_Z_4_9b.png|right|frame|PDF of the output variable $Y$ <br>with uniformly distributed noise $N$]] |
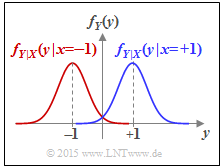
| − | '''(2)''' | + | '''(2)''' The probability density function at the output is obtained according to the equation: |
:$$f_Y(y) = {1}/{2} \cdot \big [ f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}-1) + f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}+1) \big ]\hspace{0.05cm}.$$ | :$$f_Y(y) = {1}/{2} \cdot \big [ f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}-1) + f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}+1) \big ]\hspace{0.05cm}.$$ | ||
| − | + | The graph shows the result for our example $(A = 1/8)$: | |
| − | * | + | *Drawn in red is the first term ${1}/{2} \cdot f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}-1)$, where the rectangle $f_N(n)$ is shifted to the position $y = -1$ and multiplied by $1/2$ . The result is a rectangle of width $2A = 1/4$ and height $1/(4A) = 2$. |
| − | * | + | *Shown in blue is the second term ${1}/{2} \cdot f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}+1)$ centered at $y = +1$. |
| − | * | + | *Leaving the colors out of account, the total PDF $f_Y(y)$ is obtained. |
| − | * | + | *The differential entropy is not changed by moving non-overlapping PDF sections. |
| − | * | + | *Thus, for the differential sink entropy we are looking for, we get: |
:$$h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) | :$$h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: | ||
\hspace{0.15cm}h(Y) = {\rm log}_2 \hspace{0.1cm} (1/2) | \hspace{0.15cm}h(Y) = {\rm log}_2 \hspace{0.1cm} (1/2) | ||
| − | \hspace{0.15cm}\underline{= -1\,{\rm bit(/ | + | \hspace{0.15cm}\underline{= -1\,{\rm bit(/symbol)}}\hspace{0.05cm}.$$ |
| − | '''(3)''' | + | '''(3)''' Thus, for the mutual information between source and sink, we obtain: |
| − | :$$I(X; Y) = h(Y) \hspace{-0.05cm}-\hspace{-0.05cm} h(N) = (-1\,{\rm bit/ | + | :$$I(X; Y) = h(Y) \hspace{-0.05cm}-\hspace{-0.05cm} h(N) = (-1\,{\rm bit/symbol})\hspace{-0.05cm} -\hspace{-0.05cm}(-2\,{\rm bit/symbol}) |
\hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' <u> | + | '''(4)''' <u>All the proposed solutions</u> are true: |
| − | * | + | *For each $A ≤ 1$ holds |
:$$ h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) = {\rm log}_2 \hspace{0.1cm} (2A) + {\rm log}_2 \hspace{0.1cm} (2)\hspace{0.05cm}, \hspace{0.5cm} | :$$ h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) = {\rm log}_2 \hspace{0.1cm} (2A) + {\rm log}_2 \hspace{0.1cm} (2)\hspace{0.05cm}, \hspace{0.5cm} | ||
h(N) = {\rm log}_2 \hspace{0.1cm} (2A)$$ | h(N) = {\rm log}_2 \hspace{0.1cm} (2A)$$ | ||
:$$\Rightarrow \hspace{0.3cm} I(X; Y) = h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(N) = {\rm log}_2 \hspace{0.1cm} (2) | :$$\Rightarrow \hspace{0.3cm} I(X; Y) = h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(N) = {\rm log}_2 \hspace{0.1cm} (2) | ||
\hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$ | ||
| − | * | + | *This principle does not change even if the PDF $f_N(n)$ is different, as long as the noise is limited to the range $|\hspace{0.05cm}n\hspace{0.05cm}| ≤ 1$ . |
| − | * | + | *However, if the two conditional probability density functions overlap, the result is a smaller value for $h(Y)$ than calculated above and thus smaller mutual information. |
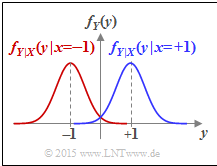
| − | [[File:EN_Inf_Z_4_9e.png|right|frame| | + | [[File:EN_Inf_Z_4_9e.png|right|frame|PDF of the output quantity $Y$ <br>with Gaussian noise $N$]] |
| − | '''(5)''' | + | '''(5)''' Correct is the <u>proposed solution 2</u>: |
| − | * | + | * The Gaussian function decays very fast, but it never becomes exactly equal to zero. |
| − | * | + | * There is always an overlap of the conditional density functions $f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.08cm}|\hspace{0.05cm}-1)$ and $f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.08cm}|\hspace{0.05cm}+1)$. |
| − | * | + | *According to subtask '''(4)''' , $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/channel\:use $ is therefore not possible. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 22:25, 1 November 2021
We assume here a binary bipolar source signal ⇒ $ x \in X = \{+1, -1\}$.
Thus, the probability density function (PDF) of the source is:
- $$f_X(x) = {1}/{2} \cdot \delta (x-1) + {1}/{2} \cdot \delta (x+1)\hspace{0.05cm}. $$
The mutual information between the source $X$ and the sink $Y$ can be calculated according to the equation
- $$I(X;Y) = h(Y) - h(N)$$
where holds:
- $h(Y)$ denotes the differential sink entropy
- $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}(f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$
- $${\rm with}\hspace{0.5cm} f_Y(y) = {1}/{2} \cdot \big[ f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}{X}=-1) + f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}{X}=+1) \big ]\hspace{0.05cm}.$$
- $h(N)$ gives the differential noise entropy computable from the PDF $f_N(n)$ alone:
- $$h(N) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}(f_N)} \hspace{-0.35cm} f_N(n) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_N(n) \big] \hspace{0.1cm}{\rm d}n \hspace{0.05cm}.$$
Assuming a Gaussian distribution $f_N(n)$ for the noise $N$ according to the upper sketch, we obtain the channel capacity $C_\text{BPSK} = I(X;Y)$, which is shown in the theory section depending on $10 \cdot \lg (E_{\rm B}/{N_0})$ .
The question to be answered is whether there is a finite $E_{\rm B}/{N_0}$ value for which $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/channel\:use $ is possible ⇒ subtask (5).
In subtasks (1) to (4) , preliminary work is done to answer this question. The uniformly distributed noise PDF $f_N(n)$ is always assumed (see sketch below):
- $$f_N(n) = \left\{ \begin{array}{c} 1/(2A) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.3cm} |\hspace{0.05cm}n\hspace{0.05cm}| < A, \\ {\rm{f\ddot{u}r}} \hspace{0.3cm} |\hspace{0.05cm}n\hspace{0.05cm}| > A. \\ \end{array} $$
Hints:
- The task belongs to the chapter AWGN channel capacitance with discrete value input.
- Reference is made in particular to the page AWGN channel capacitance for binary input signals.
Questions
Solution
- $$ h(N) = {\rm log}_2 \hspace{0.1cm} (2A) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: \hspace{0.15cm}h(N) = {\rm log}_2 \hspace{0.1cm} (1/4) \hspace{0.15cm}\underline{= -2\,{\rm bit(/symbol)}}\hspace{0.05cm}.$$
(2) The probability density function at the output is obtained according to the equation:
- $$f_Y(y) = {1}/{2} \cdot \big [ f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}-1) + f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}+1) \big ]\hspace{0.05cm}.$$
The graph shows the result for our example $(A = 1/8)$:
- Drawn in red is the first term ${1}/{2} \cdot f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}-1)$, where the rectangle $f_N(n)$ is shifted to the position $y = -1$ and multiplied by $1/2$ . The result is a rectangle of width $2A = 1/4$ and height $1/(4A) = 2$.
- Shown in blue is the second term ${1}/{2} \cdot f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}+1)$ centered at $y = +1$.
- Leaving the colors out of account, the total PDF $f_Y(y)$ is obtained.
- The differential entropy is not changed by moving non-overlapping PDF sections.
- Thus, for the differential sink entropy we are looking for, we get:
- $$h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: \hspace{0.15cm}h(Y) = {\rm log}_2 \hspace{0.1cm} (1/2) \hspace{0.15cm}\underline{= -1\,{\rm bit(/symbol)}}\hspace{0.05cm}.$$
(3) Thus, for the mutual information between source and sink, we obtain:
- $$I(X; Y) = h(Y) \hspace{-0.05cm}-\hspace{-0.05cm} h(N) = (-1\,{\rm bit/symbol})\hspace{-0.05cm} -\hspace{-0.05cm}(-2\,{\rm bit/symbol}) \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$
(4) All the proposed solutions are true:
- For each $A ≤ 1$ holds
- $$ h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) = {\rm log}_2 \hspace{0.1cm} (2A) + {\rm log}_2 \hspace{0.1cm} (2)\hspace{0.05cm}, \hspace{0.5cm} h(N) = {\rm log}_2 \hspace{0.1cm} (2A)$$
- $$\Rightarrow \hspace{0.3cm} I(X; Y) = h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(N) = {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$
- This principle does not change even if the PDF $f_N(n)$ is different, as long as the noise is limited to the range $|\hspace{0.05cm}n\hspace{0.05cm}| ≤ 1$ .
- However, if the two conditional probability density functions overlap, the result is a smaller value for $h(Y)$ than calculated above and thus smaller mutual information.
(5) Correct is the proposed solution 2:
- The Gaussian function decays very fast, but it never becomes exactly equal to zero.
- There is always an overlap of the conditional density functions $f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.08cm}|\hspace{0.05cm}-1)$ and $f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.08cm}|\hspace{0.05cm}+1)$.
- According to subtask (4) , $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/channel\:use $ is therefore not possible.