Difference between revisions of "Aufgaben:Exercise 5.3: 1st order Digital Filter"
From LNTwww
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Digital_Filters |
}} | }} | ||
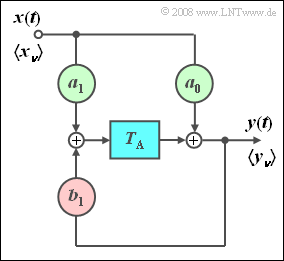
| − | [[File:P_ID607__Sto_A_5_3.png|right|frame| | + | [[File:P_ID607__Sto_A_5_3.png|right|frame|First order digital filter]] |
| − | + | We consider the filter arrangement shown on the right with coefficients $a_0$, $a_1$ and $b_1$, each of which can take values between $0$ and $1$. | |
| − | * | + | *Let the input signal $x(t)$ be a single Dirac delta impulse with unit weight "1" ⇒ $x(t) = \delta(t)$, which corresponds to the following discrete-time representation: |
:$$\left\langle {\hspace{0.05cm}x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}1,\;0,\;0,\;0,\;\text{...} \hspace{0.05cm}\right\rangle .$$ | :$$\left\langle {\hspace{0.05cm}x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}1,\;0,\;0,\;0,\;\text{...} \hspace{0.05cm}\right\rangle .$$ | ||
| − | * | + | *Due to this special input sequence, the sequence $\left\langle {\hspace{0.05cm}y_\nu \hspace{0.05cm}} \right\rangle$ at the filter output simultaneously describes the discrete-time impulse response $\left\langle {\hspace{0.05cm}h_\nu \hspace{0.05cm}} \right\rangle$ of the filter. The spacing of the samples here is $T_{\rm A} = 1 \hspace{0.05cm} \rm µ s$. |
| − | + | ||
| − | * | + | Note: |
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Digital_Filters|Digital Filters]]. | ||
| + | *The HTML5/JavaScript applet [[Applets:Digital_Filters|"Digital Filters"]] illustrates the subject matter of this chapter. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The special case $b_1 = 1$ leads to a non-recursive filter. |
| − | + | + | + With $a_0 = 1$, $a_1 = 0$ and $b_1 = 0$: $y(t) = x(t)$ is true. |
| − | + | + | + With $a_0 = 0$, $a_1 = 0.5$ and $b_1 = 0$: $y(t)$ is undistorted with respect to $x(t)$. |
| − | { | + | {Let now $a_0 = 1$, $a_1 = 0$ and $b_1 = 0.6$. Calculate the output sequence $\left\langle {y_\nu } \right\rangle$. What output value $y_3$ occurs at time $t = 3 \cdot T_{\rm A}$? |
|type="{}"} | |type="{}"} | ||
$y_3 \ = \ $ { 0.216 3% } | $y_3 \ = \ $ { 0.216 3% } | ||
| − | { | + | {Let $a_0 = 1$, $a_1 = 0$ and $b_1 = 0.6$. On which range $0$, ... , $M \cdot T_{\rm A}$ is the impulse response limited to if values smaller than $0.001$ are neglected? |
|type="{}"} | |type="{}"} | ||
$M \ = \ ${ 13 3% } | $M \ = \ ${ 13 3% } | ||
| − | { | + | {Let $a_0 = 1$ and $b_1 = 0.6$. Given the result from '''(2)''', calculate the output value $y_3$ for $a_1 = -0.5$. |
|type="{}"} | |type="{}"} | ||
$y_3 \ = \ $ { 0.036 3% } | $y_3 \ = \ $ { 0.036 3% } | ||
| Line 45: | Line 47: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solutions 2 and 3</u> are correct: |
| − | * | + | *The filter is non-recursive if the feedback is omitted: $b_1 = 0$. |
| − | * | + | *If additionally $a_0 = 1$ and $a_1 = 0$, the sequences $\left\langle {x_\nu } \right\rangle$ and $\left\langle {y_\nu } \right\rangle$ and thus of course the signals $x(t)$ and $y(t)$ are equal. |
| − | * | + | *With $a_0 = 0$ and $a_1 = 1$, $y(t) = x(t-T_{\rm A})$ is delayed by $T_{\rm A}$ with $a_1 = 0.5$ additionally attenuated. |
| − | * | + | *However, delay and damping do not result in distortion. |
| + | |||
| − | '''(2)''' | + | '''(2)''' At time $\nu = 0$: $y_{\nu} = x_{\nu} = 1$. |
| + | *For all further time points: $\nu$, $x_{\nu} = 0$ and thus: | ||
:$$y_\nu = b_1 \cdot y_{\nu - 1} = {b_1 }^\nu .$$ | :$$y_\nu = b_1 \cdot y_{\nu - 1} = {b_1 }^\nu .$$ | ||
| − | + | *In particular, $y_3 = b_1^3 = 0.6^3\hspace{0.15cm}\underline{= 0.216}$. | |
| + | |||
| − | '''(3)''' | + | '''(3)''' According to the problem definition must be valid: |
| + | :$$y_{M + 1} = {b_1} ^{M + 1} < 0.001.$$ | ||
| + | *This leads to the result: | ||
:$$M + 1 \ge \frac{{\lg \ \left( {0.001} \right)}}{{\lg \ \left( {0.6} \right)}} = \frac{ - 3}{ - 0.222} \approx 13.51\quad \Rightarrow \quad \hspace{0.15cm} \underline{M = 13}.$$ | :$$M + 1 \ge \frac{{\lg \ \left( {0.001} \right)}}{{\lg \ \left( {0.6} \right)}} = \frac{ - 3}{ - 0.222} \approx 13.51\quad \Rightarrow \quad \hspace{0.15cm} \underline{M = 13}.$$ | ||
| − | + | *Checking the values of $y_{13} \approx 0.0013$ and $y_{14} \approx 0.0008$ confirms this result. | |
| + | |||
| − | '''(4)''' | + | '''(4)''' Due to the linearity of the present filter, the same result is obtained |
| − | * | + | *if the filter is not changed compared to subtask '''(2)''' $(a_1 = 0)$ |
| − | * | + | *and the input sequence $\left\langle {x_\nu } \right\rangle = \left\langle {1,\; - 0.5,\;0,\;0,\;\text{...} } \right\rangle$ is considered. |
| − | + | One then obtains in general for $\nu \gt 0$: | |
:$$y_\nu = {b_1} ^\nu + a_1 \cdot {b_1} ^{\nu - 1} = \left( {b_1 + a_1 } \right) \cdot {b_1} ^{\nu - 1} .$$ | :$$y_\nu = {b_1} ^\nu + a_1 \cdot {b_1} ^{\nu - 1} = \left( {b_1 + a_1 } \right) \cdot {b_1} ^{\nu - 1} .$$ | ||
| − | + | *With $b_1 = 0.6$ and $a_1 = -0.5$, this gives $y_\nu = 0.1\cdot {0.6} ^{\nu - 1}$, and thus the sequence $\left\langle {y_\nu } \right\rangle = \left\langle {1,\;0.1,\;0.06,\;0.036,\;\text{...} } \right\rangle .$ | |
| − | |||
| − | + | *The value we are looking for is $y_3\hspace{0.15cm}\underline{= 0.036}$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^5.2 Digital Filters^]] |
Latest revision as of 19:00, 10 February 2022
We consider the filter arrangement shown on the right with coefficients $a_0$, $a_1$ and $b_1$, each of which can take values between $0$ and $1$.
- Let the input signal $x(t)$ be a single Dirac delta impulse with unit weight "1" ⇒ $x(t) = \delta(t)$, which corresponds to the following discrete-time representation:
- $$\left\langle {\hspace{0.05cm}x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}1,\;0,\;0,\;0,\;\text{...} \hspace{0.05cm}\right\rangle .$$
- Due to this special input sequence, the sequence $\left\langle {\hspace{0.05cm}y_\nu \hspace{0.05cm}} \right\rangle$ at the filter output simultaneously describes the discrete-time impulse response $\left\langle {\hspace{0.05cm}h_\nu \hspace{0.05cm}} \right\rangle$ of the filter. The spacing of the samples here is $T_{\rm A} = 1 \hspace{0.05cm} \rm µ s$.
Note:
- The exercise belongs to the chapter Digital Filters.
- The HTML5/JavaScript applet "Digital Filters" illustrates the subject matter of this chapter.
Questions
Solution
(1) Solutions 2 and 3 are correct:
- The filter is non-recursive if the feedback is omitted: $b_1 = 0$.
- If additionally $a_0 = 1$ and $a_1 = 0$, the sequences $\left\langle {x_\nu } \right\rangle$ and $\left\langle {y_\nu } \right\rangle$ and thus of course the signals $x(t)$ and $y(t)$ are equal.
- With $a_0 = 0$ and $a_1 = 1$, $y(t) = x(t-T_{\rm A})$ is delayed by $T_{\rm A}$ with $a_1 = 0.5$ additionally attenuated.
- However, delay and damping do not result in distortion.
(2) At time $\nu = 0$: $y_{\nu} = x_{\nu} = 1$.
- For all further time points: $\nu$, $x_{\nu} = 0$ and thus:
- $$y_\nu = b_1 \cdot y_{\nu - 1} = {b_1 }^\nu .$$
- In particular, $y_3 = b_1^3 = 0.6^3\hspace{0.15cm}\underline{= 0.216}$.
(3) According to the problem definition must be valid:
- $$y_{M + 1} = {b_1} ^{M + 1} < 0.001.$$
- This leads to the result:
- $$M + 1 \ge \frac{{\lg \ \left( {0.001} \right)}}{{\lg \ \left( {0.6} \right)}} = \frac{ - 3}{ - 0.222} \approx 13.51\quad \Rightarrow \quad \hspace{0.15cm} \underline{M = 13}.$$
- Checking the values of $y_{13} \approx 0.0013$ and $y_{14} \approx 0.0008$ confirms this result.
(4) Due to the linearity of the present filter, the same result is obtained
- if the filter is not changed compared to subtask (2) $(a_1 = 0)$
- and the input sequence $\left\langle {x_\nu } \right\rangle = \left\langle {1,\; - 0.5,\;0,\;0,\;\text{...} } \right\rangle$ is considered.
One then obtains in general for $\nu \gt 0$:
- $$y_\nu = {b_1} ^\nu + a_1 \cdot {b_1} ^{\nu - 1} = \left( {b_1 + a_1 } \right) \cdot {b_1} ^{\nu - 1} .$$
- With $b_1 = 0.6$ and $a_1 = -0.5$, this gives $y_\nu = 0.1\cdot {0.6} ^{\nu - 1}$, and thus the sequence $\left\langle {y_\nu } \right\rangle = \left\langle {1,\;0.1,\;0.06,\;0.036,\;\text{...} } \right\rangle .$
- The value we are looking for is $y_3\hspace{0.15cm}\underline{= 0.036}$.