Difference between revisions of "Aufgaben:Exercise 5.3Z: Zero-Padding"
m (Oezdemir moved page Aufgabe 5.3Z: Zero-Padding to Exercise 5.3Z: Zero-Padding) |
|||
| Line 4: | Line 4: | ||
[[File:P_ID1146__Sig_Z_5_3_neu.png|right|frame|$\rm MQF$–Werte als Funktion von $T_{\rm A} /T$ und $N$]] | [[File:P_ID1146__Sig_Z_5_3_neu.png|right|frame|$\rm MQF$–Werte als Funktion von $T_{\rm A} /T$ und $N$]] | ||
| − | + | We consider the DFT of a rectangular pulse $x(t)$ of height $A =1$ and duration $T$. Thus the spectral function $X(f)$ a $\sin(f)/f$–shaped course. | |
| − | + | For this special case the influence of the DFT parameter $N$ is to be analysed, whereby the interpolation point distance in the time domain should always be $T_{\rm A} = 0.01T$ bzw. $T_{\rm A} = 0.05T$ . | |
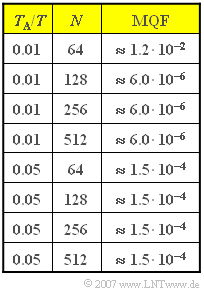
| − | + | The resulting values for the ''mean square error'' (MSE, here MQF) of the grid values in the frequency domain are given opposite for different values of $N$ : | |
:$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | :$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | ||
\left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | ||
| − | + | Thus, for $T_A/T = 0.01$ , $101$ of the DFT coefficients $d(ν)$ are always different from zero. | |
| − | :* | + | :* Of these, $99$ have the value $1$ and the two marginal coefficients are each equal to $0.5$. |
| − | :* | + | :* If $N$, is increased, the DFT coefficient field is filled with zeros. |
| − | :* | + | :*This is then referred to as ''„zero padding”''. |
| Line 27: | Line 27: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This task belongs to the chapter [[Signal_Representation/Possible_Errors_When_Using_DFT|Possible Errors when Using DFT]]. |
| − | * | + | *The theory of this chapter is summarised in the learning video [[Fehlermöglichkeiten_bei_Anwendung_der_DFT_(Lernvideo)|Possible Errors when Using DFT]] . |
| Line 36: | Line 36: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements can be derived from the given MQF values $($valid for $T_{\rm A}/T = 0.01$ and $N ≥ 128)$ abgeleitet werden? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The $\rm MQF$ value here is almost independent o $N$. |
| − | - | + | - The $\rm MQF$ value is determined by the termination error. |
| − | + | + | + The $\rm MQF$ value is determined by the aliasing error. |
| − | { | + | {Let $T_{\rm A}/T = 0.01$. What is the distance $f_{\rm A}$ of adjacent samples in the frequency domain for $N = 128$ and $N = 512$? |
|type="{}"} | |type="{}"} | ||
$N = 128$: $f_{\rm A} \cdot T \ = \ $ { 0.781 3% } | $N = 128$: $f_{\rm A} \cdot T \ = \ $ { 0.781 3% } | ||
| Line 52: | Line 52: | ||
| − | { | + | {What does the product $\text{MQF} \cdot f_{\rm A}$ indicate in terms of DFT quality? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The product $\text{MQF} \cdot f_{\rm A}$ considers the accuracy and density of the DFT values. |
| − | - | + | - The product $\text{MQF} \cdot f_{\rm A}$ should be as large as possible. |
| − | + | { $N = 128$ is now fixed. Which statements apply to the comparison of the DFT results with $T_{\rm A}/T = 0.01$ und $T_{\rm A}/T = 0.05$ ? | |
| − | { | ||
|type="[]"} | |type="[]"} | ||
| − | + Mit $T_{\rm A}/T = 0.05$ | + | + Mit $T_{\rm A}/T = 0.05$ you get a finer frequency resolution. |
| − | - Mit $T_{\rm A}/T = 0.05$ | + | - Mit $T_{\rm A}/T = 0.05$ the $\rm MQF$ value is smaller. |
| − | - Mit $T_{\rm A}/T = 0.05$ | + | - Mit $T_{\rm A}/T = 0.05$ the influence of the termination error decreases. |
| − | + Mit $T_{\rm A}/T = 0.05$ | + | + Mit $T_{\rm A}/T = 0.05$ the influence of the aliasing error increases. |
| − | { | + | {Now $N = 64$.Which statements are true for the comparison of the DFT results with $T_{\rm A}/T = 0.01$ und $T_{\rm A}/T = 0.05$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + With $T_{\rm A}/T = 0.05$ you get a finer frequency resolution. |
| − | + | + | + With $T_{\rm A}/T = 0.05$ the $\rm MQF$ value is smaller. |
| − | + | + | + With $T_{\rm A}/T = 0.05$ the influence of the termination error decreases. |
| − | + | + | + With $T_{\rm A}/T = 0.05$ the influence of the aliasing error increases. |
| Line 77: | Line 76: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
Revision as of 16:01, 22 March 2021
We consider the DFT of a rectangular pulse $x(t)$ of height $A =1$ and duration $T$. Thus the spectral function $X(f)$ a $\sin(f)/f$–shaped course.
For this special case the influence of the DFT parameter $N$ is to be analysed, whereby the interpolation point distance in the time domain should always be $T_{\rm A} = 0.01T$ bzw. $T_{\rm A} = 0.05T$ .
The resulting values for the mean square error (MSE, here MQF) of the grid values in the frequency domain are given opposite for different values of $N$ :
- $${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
Thus, for $T_A/T = 0.01$ , $101$ of the DFT coefficients $d(ν)$ are always different from zero.
- Of these, $99$ have the value $1$ and the two marginal coefficients are each equal to $0.5$.
- If $N$, is increased, the DFT coefficient field is filled with zeros.
- This is then referred to as „zero padding”.
Hints:
- This task belongs to the chapter Possible Errors when Using DFT.
- The theory of this chapter is summarised in the learning video Possible Errors when Using DFT .
Questions
Solution
- Bereits mit $N = 128$ ist $T_{\rm P} = 1.28 \cdot T$, also größer als die Breite des Rechtecks.
- Somit spielt hier der Abbruchfehler überhaupt keine Rolle.
- Der $\rm MQF$–Wert wird allein durch den Aliasingfehler bestimmt.
- Die Zahlenwerte bestätigen eindeutig, dass $\rm MQF$ (nahezu) unabhängig von $N$ ist.
(2) Aus $T_{\rm A}/T = 0.01$ folgt $f_{\rm P} \cdot T = 100$.
- Die Stützwerte von $X(f)$ liegen also im Bereich $–50 ≤ f \cdot T < +50$.
- Für den Abstand zweier Abtastwerte im Frequenzbereich gilt $f_{\rm A} = f_{\rm P}/N$. Daraus ergeben sich folgende Ergebnisse:
- $N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$,
- $N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$.
(3) Richtig ist die erste Aussage:
- Für $N = 128$ ergibt sich für das Produkt $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{-6}/T$. Für $N = 512$ ist das Produkt etwa um den Faktor $4$ kleiner.
- Das heißt: Durch „Zero–Padding” wird keine größere DFT-Genauigkeit erzielt, dafür aber eine feinere „Auflösung” des Frequenzbereichs.
- Das Produkt $\text{MQF} \cdot f_{\rm A}$ berücksichtigt diese Tatsache; es sollte stets möglichst klein sein.
(4) Richtig sind die Lösungsvorschläge 1 und 4:
- Wegen $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ ergibt sich bei konstantem $N$ immer dann ein kleinerer $f_{\rm A}$–Wert, wenn man $T_{\rm A}$ vergrößert.
- Aus der Tabelle auf der Angabenseite erkennt man, dass damit der mittlere quadratische Fehler $\rm (MQF)$ signifikant $($etwa um den Faktor $400)$ vergrößert wird.
- Der Effekt geht auf den Aliasingfehler zurück, da durch den Übergang von $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ die Frequenzperiode um den Faktor $5$ kleiner wird.
- Der Abbruchfehler spielt dagegen beim Rechteckimpuls weiterhin keine Rolle, solange $T_{\rm P} = N \cdot T_{\rm A}$ größer ist als die Impulsdauer $T$.
(5) Alle Aussagen treffen zu:
- Mit den Parameterwerten $N = 64$ und $T_{\rm A}/T = 0.01$ tritt ein extrem großer Abbruchfehler auf.
- Alle Zeitkoeffizienten sind hier $1$, so dass die DFT fälschlicherweise ein Gleichsignal anstelle der Rechteckfunktion interpretiert.