Difference between revisions of "Aufgaben:Exercise 5.5: ACF-equivalent Filters"
From LNTwww
| (15 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Creation_of_Predefined_ACF_Properties |
}} | }} | ||
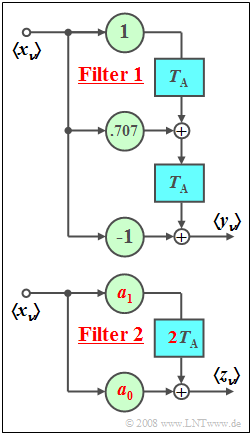
| − | [[File:P_ID558__Sto_A_5_5_neu.png|right|frame| | + | [[File:P_ID558__Sto_A_5_5_neu.png|right|frame|Two ACF–equivalent filters]] |
| − | + | We consider the two digital filters outlined: | |
| − | * | + | * The individual elements of the input sequence $\left\langle {x_\nu } \right\rangle$ are in both cases statistically independent of each other and equally distributed between $-1$ and $+1$. |
| − | * | + | * It follows directly for the mean and the variance: |
:$$m_x = 0,\quad \sigma _x^2 = {1}/{3}.$$ | :$$m_x = 0,\quad \sigma _x^2 = {1}/{3}.$$ | ||
| − | + | *The delay times of $\text{Filter 1}$ are equal to $T_{\rm A} = 1 \hspace{0.05cm} \rm µ s$ in each case. The delays of $\text{Filter 2}$ are twice as long. | |
| − | + | *The coefficients $a_0$ and $a_1$ of $\text{Filter 2}$ should be set so that the auto-correlation functions $\rm (ACFs)$ of $\left\langle {y_\nu } \right\rangle$ and of $\left\langle {z_\nu } \right\rangle$ match exactly. If there are multiple solutions, please choose the one with $|a_1| < |a_0|$. | |
| − | + | Notes: | |
| − | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Creation_of_Predefined_ACF_Properties|Creation of Predefined ACF Properties]]. | |
| − | + | *The coefficients of $\text{Filter 1}$ are denoted by $\alpha_0$, $\alpha_1$, $\alpha_2$ ("alphas") in the questions. | |
| − | * | ||
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true regarding $\text{Filter 1}$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It is a non-recursive filter. |
| − | + | + | + The order of the filter is $M = 2$. |
| − | - | + | - The upper filter coefficient is equal to $\alpha_0 =+1$. |
| − | { | + | {Calculate the standard deviation of the output sequence $\left\langle {y_\nu } \right\rangle$. |
|type="{}"} | |type="{}"} | ||
$\sigma_y \ = \ $ { 0.913 3% } | $\sigma_y \ = \ $ { 0.913 3% } | ||
| − | { | + | {Calculate the ACF values $\varphi_y(k \cdot T_{\rm A})$ for $k = 1$ and $k = 2$. |
|type="{}"} | |type="{}"} | ||
$\varphi_y(T_{\rm A}) \ = \ $ { 0. } | $\varphi_y(T_{\rm A}) \ = \ $ { 0. } | ||
| Line 46: | Line 44: | ||
| − | { | + | {Determine the coefficients of $\text{Filter 2}$ such that $\left\langle {z_\nu } \right\rangle$ and $\left\langle {y_\nu } \right\rangle$ have the same ACF. What is the quotient $a_1/a_0$ for $|a_1| < |a_0|$? |
|type="{}"} | |type="{}"} | ||
$a_1/a_0 \ = \ $ { -0.515--0.485 } | $a_1/a_0 \ = \ $ { -0.515--0.485 } | ||
| − | { | + | {Which statements are true for the probability density functions? |
|type="[]"} | |type="[]"} | ||
| − | - $f_y(y)$ | + | - $f_y(y)$ and $f_z(z)$ are identical. |
| − | + $f_y(y)$ | + | + $f_y(y)$ and $f_z(z)$ are different in general. |
| − | + | + | + With Gaussian input, $f_y(y)$ and $f_z(z)$ would be the same. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>The first two solutions</u> are correct: |
| − | * | + | *It is a second-order non-recursive filter with coefficients $\alpha_0 = -1$, $\alpha_1 = +0.707$ and $\alpha_2 = +1$. |
| − | * | + | *The coefficients of $\text{Filter 1}$ are denoted here as $\alpha_0$, $\alpha_1$, $\alpha_2$ ("alphas"). |
| − | '''(2)''' | + | |
| + | '''(2)''' The variance of the output values is equal to the ACF value for $k = 0$. For this one obtains: | ||
:$$\varphi _y (0) = \sigma _x ^2 \cdot \left( {\alpha _0 ^2 + \alpha _1 ^2 + \alpha _2 ^2 } \right) = {1}/{3} \cdot \left( {1 + {1}/{2} + 1} \right) = 0.833.$$ | :$$\varphi _y (0) = \sigma _x ^2 \cdot \left( {\alpha _0 ^2 + \alpha _1 ^2 + \alpha _2 ^2 } \right) = {1}/{3} \cdot \left( {1 + {1}/{2} + 1} \right) = 0.833.$$ | ||
| − | + | *This gives the standard deviation: | |
:$$\sigma _y = \sqrt {\varphi _y (0)} \hspace{0.15cm} \underline{= 0.913}.$$ | :$$\sigma _y = \sqrt {\varphi _y (0)} \hspace{0.15cm} \underline{= 0.913}.$$ | ||
| − | '''(3)''' | + | |
| + | |||
| + | '''(3)''' These two ACF values can be calculated as follows: | ||
:$$\varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _1 + \alpha _1 \cdot \alpha _2 } \right) = {1}/{3} \cdot \left( { - 1 \cdot 0.707 + 0.707 \cdot 1} \right) \hspace{0.15cm} \underline{= 0},$$ | :$$\varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _1 + \alpha _1 \cdot \alpha _2 } \right) = {1}/{3} \cdot \left( { - 1 \cdot 0.707 + 0.707 \cdot 1} \right) \hspace{0.15cm} \underline{= 0},$$ | ||
:$$\varphi _y ( {2T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _2 } \right) = -1/3\hspace{0.15cm} \underline{\approx - 0.333}.$$ | :$$\varphi _y ( {2T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _2 } \right) = -1/3\hspace{0.15cm} \underline{\approx - 0.333}.$$ | ||
| − | '''(4)''' | + | |
| + | |||
| + | '''(4)''' Because of $\varphi _y ( {T_{\rm A} } )= 0$, if $a_0$ and $a_1$ are chosen appropriately, it is possible that the ACF at the output of $\text{Filter 2}$ is identical to the ACF calculated in '''(3)'''. | ||
| + | *With $T_{\rm A}\hspace{0.05cm}' = 2 \cdot T_{\rm A}$ holds: | ||
:$$\varphi _z (0) = {1}/{3} \cdot \left( {a_0 ^2 + a_1 ^2 } \right) = 0.833\quad \Rightarrow \quad a_0 ^2 + a_1 ^2 = 2.5, $$ | :$$\varphi _z (0) = {1}/{3} \cdot \left( {a_0 ^2 + a_1 ^2 } \right) = 0.833\quad \Rightarrow \quad a_0 ^2 + a_1 ^2 = 2.5, $$ | ||
| − | :$$\varphi _z( { | + | :$$\varphi _z( {T_{\rm A} \hspace{0.05cm}'} ) = {1}/{3}\left( {a_0 \cdot a_1 } \right) = - {1}/{3}\quad \;\;\, \Rightarrow \quad a_0 \cdot a_1 = - 1.$$ |
| − | + | *With the auxiliary quantity $H = a_0^2$ this leads to the equation of determination: | |
:$$H + {1}/{H} = 2.5\quad \Rightarrow \quad H^2 - 2.5 \cdot H + 1 = 0$$ | :$$H + {1}/{H} = 2.5\quad \Rightarrow \quad H^2 - 2.5 \cdot H + 1 = 0$$ | ||
:$$\Rightarrow \hspace{0.3cm}H_{1/2} = {1}/{2} \cdot \left( {2.5 \pm \sqrt {2.5^2 - 4} } \right) = {1}/{2} \cdot \left( {2.5 \pm 1.5} \right).$$ | :$$\Rightarrow \hspace{0.3cm}H_{1/2} = {1}/{2} \cdot \left( {2.5 \pm \sqrt {2.5^2 - 4} } \right) = {1}/{2} \cdot \left( {2.5 \pm 1.5} \right).$$ | ||
| − | + | *The two solutions are $H_1 = 2$ and $H_2 = 1/2$. This gives four possible solutions: | |
:$$a_0 = \sqrt 2 ,\quad \;\;\, a_1 = - {1}/{\sqrt 2 }, | :$$a_0 = \sqrt 2 ,\quad \;\;\, a_1 = - {1}/{\sqrt 2 }, | ||
\hspace{2cm} a_0 = - \sqrt 2 ,\quad a_1 = {1}/{\sqrt 2 },$$ | \hspace{2cm} a_0 = - \sqrt 2 ,\quad a_1 = {1}/{\sqrt 2 },$$ | ||
| Line 90: | Line 94: | ||
\hspace{2cm} a_0 = - {1}/{\sqrt 2 },\quad a_1 = \sqrt 2 .$$ | \hspace{2cm} a_0 = - {1}/{\sqrt 2 },\quad a_1 = \sqrt 2 .$$ | ||
| − | + | *For the last two pairs of solutions, the condition $|a_1| < |a_0|$ is not satisfied. On the other hand, for the upper equations, in both cases: | |
:$$ \hspace{0.15cm} \underline{a_1 /a_0 = - 0.5}.$$ | :$$ \hspace{0.15cm} \underline{a_1 /a_0 = - 0.5}.$$ | ||
| − | '''(5)''' | + | |
| − | * | + | |
| − | *$f_z(z)$ | + | '''(5)''' <u>The solutions 2 and 3</u> are correct: |
| − | * | + | *In general $($even with equally distributed input variable $x)$ the probability density functions $f_y(y)$ and $f_z(z)$ are different. |
| + | *In this case, $f_z(z)$ results from the convolution of two rectangles of different width; thus, it is trapezoidal. | ||
| + | *To calculate $f_y(y)$, on the other hand, three rectangles would have to be folded together. | ||
| + | *With Gaussian input $x$: $y$ and $z$ are also Gaussian distributed, and because of $m_y = m_z$ and $\sigma_y = \sigma_z$, $f_z(z) = f_y(y)$ is also valid. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^5.3 Filter Matching to ACF^]] |
Latest revision as of 17:18, 17 February 2022
We consider the two digital filters outlined:
- The individual elements of the input sequence $\left\langle {x_\nu } \right\rangle$ are in both cases statistically independent of each other and equally distributed between $-1$ and $+1$.
- It follows directly for the mean and the variance:
- $$m_x = 0,\quad \sigma _x^2 = {1}/{3}.$$
- The delay times of $\text{Filter 1}$ are equal to $T_{\rm A} = 1 \hspace{0.05cm} \rm µ s$ in each case. The delays of $\text{Filter 2}$ are twice as long.
- The coefficients $a_0$ and $a_1$ of $\text{Filter 2}$ should be set so that the auto-correlation functions $\rm (ACFs)$ of $\left\langle {y_\nu } \right\rangle$ and of $\left\langle {z_\nu } \right\rangle$ match exactly. If there are multiple solutions, please choose the one with $|a_1| < |a_0|$.
Notes:
- The exercise belongs to the chapter Creation of Predefined ACF Properties.
- The coefficients of $\text{Filter 1}$ are denoted by $\alpha_0$, $\alpha_1$, $\alpha_2$ ("alphas") in the questions.
Questions
Solution
(1) The first two solutions are correct:
- It is a second-order non-recursive filter with coefficients $\alpha_0 = -1$, $\alpha_1 = +0.707$ and $\alpha_2 = +1$.
- The coefficients of $\text{Filter 1}$ are denoted here as $\alpha_0$, $\alpha_1$, $\alpha_2$ ("alphas").
(2) The variance of the output values is equal to the ACF value for $k = 0$. For this one obtains:
- $$\varphi _y (0) = \sigma _x ^2 \cdot \left( {\alpha _0 ^2 + \alpha _1 ^2 + \alpha _2 ^2 } \right) = {1}/{3} \cdot \left( {1 + {1}/{2} + 1} \right) = 0.833.$$
- This gives the standard deviation:
- $$\sigma _y = \sqrt {\varphi _y (0)} \hspace{0.15cm} \underline{= 0.913}.$$
(3) These two ACF values can be calculated as follows:
- $$\varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _1 + \alpha _1 \cdot \alpha _2 } \right) = {1}/{3} \cdot \left( { - 1 \cdot 0.707 + 0.707 \cdot 1} \right) \hspace{0.15cm} \underline{= 0},$$
- $$\varphi _y ( {2T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _2 } \right) = -1/3\hspace{0.15cm} \underline{\approx - 0.333}.$$
(4) Because of $\varphi _y ( {T_{\rm A} } )= 0$, if $a_0$ and $a_1$ are chosen appropriately, it is possible that the ACF at the output of $\text{Filter 2}$ is identical to the ACF calculated in (3).
- With $T_{\rm A}\hspace{0.05cm}' = 2 \cdot T_{\rm A}$ holds:
- $$\varphi _z (0) = {1}/{3} \cdot \left( {a_0 ^2 + a_1 ^2 } \right) = 0.833\quad \Rightarrow \quad a_0 ^2 + a_1 ^2 = 2.5, $$
- $$\varphi _z( {T_{\rm A} \hspace{0.05cm}'} ) = {1}/{3}\left( {a_0 \cdot a_1 } \right) = - {1}/{3}\quad \;\;\, \Rightarrow \quad a_0 \cdot a_1 = - 1.$$
- With the auxiliary quantity $H = a_0^2$ this leads to the equation of determination:
- $$H + {1}/{H} = 2.5\quad \Rightarrow \quad H^2 - 2.5 \cdot H + 1 = 0$$
- $$\Rightarrow \hspace{0.3cm}H_{1/2} = {1}/{2} \cdot \left( {2.5 \pm \sqrt {2.5^2 - 4} } \right) = {1}/{2} \cdot \left( {2.5 \pm 1.5} \right).$$
- The two solutions are $H_1 = 2$ and $H_2 = 1/2$. This gives four possible solutions:
- $$a_0 = \sqrt 2 ,\quad \;\;\, a_1 = - {1}/{\sqrt 2 }, \hspace{2cm} a_0 = - \sqrt 2 ,\quad a_1 = {1}/{\sqrt 2 },$$
- $$a_0 = {1}/{\sqrt 2 },\quad \;\,\, a_1 = - \sqrt 2 , \hspace{2cm} a_0 = - {1}/{\sqrt 2 },\quad a_1 = \sqrt 2 .$$
- For the last two pairs of solutions, the condition $|a_1| < |a_0|$ is not satisfied. On the other hand, for the upper equations, in both cases:
- $$ \hspace{0.15cm} \underline{a_1 /a_0 = - 0.5}.$$
(5) The solutions 2 and 3 are correct:
- In general $($even with equally distributed input variable $x)$ the probability density functions $f_y(y)$ and $f_z(z)$ are different.
- In this case, $f_z(z)$ results from the convolution of two rectangles of different width; thus, it is trapezoidal.
- To calculate $f_y(y)$, on the other hand, three rectangles would have to be folded together.
- With Gaussian input $x$: $y$ and $z$ are also Gaussian distributed, and because of $m_y = m_z$ and $\sigma_y = \sigma_z$, $f_z(z) = f_y(y)$ is also valid.