Difference between revisions of "Aufgaben:Exercise 5.6: Error Correlation Duration"
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Burst_Error_Channels}} |
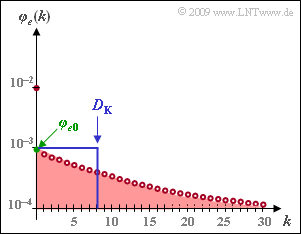
| − | [[File:P_ID1842__Dig_A_5_6.png|right|frame| | + | [[File:P_ID1842__Dig_A_5_6.png|right|frame|Error correlation function of the GE model]] |
| − | + | The graph shows the ''error correlation function'' (ECF) of the ''Gilbert–Elliott model'' with the parameters | |
:$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, | :$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, | ||
| − | \hspace{0.2cm}p_{\rm B} = 0.1, | + | \hspace{0.2cm}p_{\rm B} = 0.1,\hspace{0.2cm} |
| − | + | {\rm Pr}(\rm | |
G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ | G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ | ||
\hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm | \hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm | ||
B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}$$ | B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}$$ | ||
| − | in | + | in logarithmic representation. |
| − | + | This model is discussed in detail in [[Aufgaben:Exercise_5.6Z:_Gilbert-Elliott_Model|"Exercise 5.6Z"]]. In particular, the error correlation function (ECF) is also calculated in this exercise. With the auxiliary quantities | |
:$$A \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (p_{\rm B}- p_{\rm M}) | :$$A \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (p_{\rm B}- p_{\rm M}) | ||
\cdot (p_{\rm M}- p_{\rm | \cdot (p_{\rm M}- p_{\rm | ||
| Line 21: | Line 21: | ||
G\hspace{0.05cm}|\hspace{0.05cm} B)$$ | G\hspace{0.05cm}|\hspace{0.05cm} B)$$ | ||
| + | it can be written for: | ||
| + | :$$\varphi_{e}(k) = | ||
| + | \left\{ \begin{array}{c} p_{\rm M} \\ | ||
| + | p_{\rm M}^2 + A \cdot (1-B)^k \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, | ||
| + | \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}$$ | ||
| + | This is a burst error channel. To quantitatively describe the statistical bonds, one often uses the correlation term according to the following definition: | ||
| + | :$$D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 | ||
| + | }^{\infty}\hspace{0.1cm}\big [\varphi_{e}(k) - p_{\rm | ||
| + | M}^2 \big]\hspace{0.05cm}.$$ | ||
| − | === | + | The reference value $\varphi_{e0}$ is obtained by <i>extrapolation</i> of the error correlation function to the point $k = 0$. If, as here, the ECF curve is given analytically, $\varphi_{e0}$ can also be calculated by inserting the value $k = 0$ into the equation which is actually only valid for $k > 0$. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Notes:'' | ||
| + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Burst_Error_Channels| "Burst Error Channels"]]. | ||
| + | *Reference is made in particular to the section [[Digital_Signal_Transmission/Burst_Error_Channels#Error_correlation_function_of_the_Gilbert-Elliott_model|"Error correlation function of the Gilbert-Elliott model"]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which ECF value is exactly valid for $k = 0$? |
| − | |type=" | + | |type="{}"} |
| − | + | + | $\varphi_e(k = 0) \ = \ ${ 1 3% } $\ \cdot 10^{-2}$ |
| − | - | + | |
| + | {What is the value extrapolated from the given ECF for $k = 0$? | ||
| + | |type="{}"} | ||
| + | $\varphi_{e0} \ = \ ${ 0.091 3% } $\ \cdot 10^{-2}$ | ||
| + | |||
| + | {What result is obtained for the error correlation duration $D_{\rm K}$ with the quantities $A$ and $B$ defined in front? | ||
| + | |type="()"} | ||
| + | - $D_{\rm K} = A \cdot B$, | ||
| + | - $D_{\rm K} = 1/A \, - B$, | ||
| + | + $D_{\rm K} = 1/B \, -1$. | ||
| − | { | + | {What is the correlation duration for the GE model at hand? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $D_{\rm K} \ = \ ${ 8.091 3% } |
| + | |||
| + | {Which statements are valid regarding the correlation duration $D_{\rm K}$ of the GE model? Note the logarithmic ordinate for your answer. | ||
| + | |type="[]"} | ||
| + | + $D_{\rm K}$ remains the same if ${\rm Pr}({\rm B\hspace{0.05cm}|\hspace{0.05cm}G})$ and ${\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}B)}$ are interchanged. | ||
| + | - $D_{\rm K}$ depends only on the sum ${\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}B) + Pr(B\hspace{0.05cm}|\hspace{0.05cm}G)}$. | ||
| + | - The red area in the graph is equal to the blue rectangular area. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The ECF value $\varphi_e(k = 0)$ always indicates the mean error probability $p_{\rm M}$, while the ECF limit for $k → ∞$ is equal to $p_{\rm M}^2$. |
| − | '''(2)''' | + | *From the graph on the information section, one can read $p_{\rm M} \ \underline {= 0.01}$. |
| − | '''(3)''' | + | *In [[Aufgaben:Exercise_5.6Z:_Gilbert-Elliott_Model|"Exercise 5.6Z"]], this value is calculated in a different way. |
| − | '''(4)''' | + | |
| − | '''(5)''' | + | |
| + | |||
| + | '''(2)''' If we insert the parameter $k = 0$ into the lower ECF equation, which is actually only valid for $k > 0$, we obtain the extrapolation value we are looking for. | ||
| + | :$$\varphi_{e0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm M}^2 + | ||
| + | (p_{\rm B}- p_{\rm M}) \cdot (p_{\rm M}- p_{\rm | ||
| + | G})\hspace{0.05cm} = 10^{-4} + | ||
| + | (0.1- 0.01) \cdot (0.01- 0.001)=10^{-4} + 0.09 \cdot 0.009 | ||
| + | \hspace{0.15cm}\underline {\approx 0.091 \cdot 10^{-2}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' According to the general definition equation, the following holds for the error correlation period | ||
| + | :$$D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 | ||
| + | }^{\infty}\hspace{0.1cm} [\varphi_{e}(k) - p_{\rm | ||
| + | M}^2]\hspace{0.05cm}.$$ | ||
| + | |||
| + | *With the expressions | ||
| + | :$$A \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (p_{\rm B}- p_{\rm M}) | ||
| + | \cdot (p_{\rm M}- p_{\rm | ||
| + | G}) = \varphi_{e0} - p_{\rm M}^2\hspace{0.05cm},$$ | ||
| + | :$$B\hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G) + {\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B)$$ | ||
| + | |||
| + | :this equation can be written as follows: | ||
| + | :$$D_{\rm K} = {1}/{A} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm} | ||
| + | A \cdot (1 - B)^k = \sum_{k = 1 }^{\infty}\hspace{0.1cm} (1 - | ||
| + | B)^k\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Using the summation formula of a geometric series, this gives the final result: | ||
| + | :$$D_{\rm K} = {1}/{B} - 1 = \frac{1}{{\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G) + {\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B)} - 1\hspace{0.05cm}.$$ | ||
| + | |||
| + | *So <u>solution 3</u> is correct. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' With ${\rm Pr(B|G)} = 0.01$ and ${\rm Pr(G|B)} = 0.1$ we get | ||
| + | :$$D_{\rm K} = \frac{1}{0.01 + 0.1} - 1 \hspace{0.15cm}\underline {\approx 8.091}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Only <u>solution 1</u> is correct, as shown in the sample solutions to the last subtasks: | ||
| + | *Thus the correlation term is fixed, for example: | ||
| + | *With ${\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G)} = 0.1$ and $\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}B) = 0.01$ we get the same $D_{\rm K} = 8.091$ as with $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G) = 0.01$ and $\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}B) = 0.1$. | ||
| + | *But now the mean error probability $p_{\rm M} \approx 9.1\%$ instead of $1\%$, respectively for $p_{\rm G} = 0.001$ and $p_{\rm B} = 0.1$. | ||
| + | *The last statement is also false. This statement would only be true if $\varphi_e(k)$ was plotted linearly and not logarithmically as here. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^5.3 Burst Error Channels^]] |
Latest revision as of 14:22, 19 October 2022
The graph shows the error correlation function (ECF) of the Gilbert–Elliott model with the parameters
- $$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,\hspace{0.2cm} {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}$$
in logarithmic representation.
This model is discussed in detail in "Exercise 5.6Z". In particular, the error correlation function (ECF) is also calculated in this exercise. With the auxiliary quantities
- $$A \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (p_{\rm B}- p_{\rm M}) \cdot (p_{\rm M}- p_{\rm G})\hspace{0.05cm},$$
- $$B\hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)$$
it can be written for:
- $$\varphi_{e}(k) = \left\{ \begin{array}{c} p_{\rm M} \\ p_{\rm M}^2 + A \cdot (1-B)^k \end{array} \right.\quad \begin{array}{*{1}c} f{\rm or }\hspace{0.15cm}k = 0 \hspace{0.05cm}, \\ f{\rm or }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}$$
This is a burst error channel. To quantitatively describe the statistical bonds, one often uses the correlation term according to the following definition:
- $$D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm}\big [\varphi_{e}(k) - p_{\rm M}^2 \big]\hspace{0.05cm}.$$
The reference value $\varphi_{e0}$ is obtained by extrapolation of the error correlation function to the point $k = 0$. If, as here, the ECF curve is given analytically, $\varphi_{e0}$ can also be calculated by inserting the value $k = 0$ into the equation which is actually only valid for $k > 0$.
Notes:
- The exercise belongs to the chapter "Burst Error Channels".
- Reference is made in particular to the section "Error correlation function of the Gilbert-Elliott model".
Questions
Solution
- From the graph on the information section, one can read $p_{\rm M} \ \underline {= 0.01}$.
- In "Exercise 5.6Z", this value is calculated in a different way.
(2) If we insert the parameter $k = 0$ into the lower ECF equation, which is actually only valid for $k > 0$, we obtain the extrapolation value we are looking for.
- $$\varphi_{e0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm M}^2 + (p_{\rm B}- p_{\rm M}) \cdot (p_{\rm M}- p_{\rm G})\hspace{0.05cm} = 10^{-4} + (0.1- 0.01) \cdot (0.01- 0.001)=10^{-4} + 0.09 \cdot 0.009 \hspace{0.15cm}\underline {\approx 0.091 \cdot 10^{-2}}\hspace{0.05cm}.$$
(3) According to the general definition equation, the following holds for the error correlation period
- $$D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm} [\varphi_{e}(k) - p_{\rm M}^2]\hspace{0.05cm}.$$
- With the expressions
- $$A \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (p_{\rm B}- p_{\rm M}) \cdot (p_{\rm M}- p_{\rm G}) = \varphi_{e0} - p_{\rm M}^2\hspace{0.05cm},$$
- $$B\hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)$$
- this equation can be written as follows:
- $$D_{\rm K} = {1}/{A} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm} A \cdot (1 - B)^k = \sum_{k = 1 }^{\infty}\hspace{0.1cm} (1 - B)^k\hspace{0.05cm}.$$
- Using the summation formula of a geometric series, this gives the final result:
- $$D_{\rm K} = {1}/{B} - 1 = \frac{1}{{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)} - 1\hspace{0.05cm}.$$
- So solution 3 is correct.
(4) With ${\rm Pr(B|G)} = 0.01$ and ${\rm Pr(G|B)} = 0.1$ we get
- $$D_{\rm K} = \frac{1}{0.01 + 0.1} - 1 \hspace{0.15cm}\underline {\approx 8.091}\hspace{0.05cm}.$$
(5) Only solution 1 is correct, as shown in the sample solutions to the last subtasks:
- Thus the correlation term is fixed, for example:
- With ${\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G)} = 0.1$ and $\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}B) = 0.01$ we get the same $D_{\rm K} = 8.091$ as with $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G) = 0.01$ and $\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}B) = 0.1$.
- But now the mean error probability $p_{\rm M} \approx 9.1\%$ instead of $1\%$, respectively for $p_{\rm G} = 0.001$ and $p_{\rm B} = 0.1$.
- The last statement is also false. This statement would only be true if $\varphi_e(k)$ was plotted linearly and not logarithmically as here.