Difference between revisions of "Aufgaben:Exercise 5.7: McCullough and Gilbert-Elliott Parameters"
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Burst_Error_Channels}} |
| − | [[File: | + | [[File:EN Dig A 5 7.png|right|frame|Gilbert-Elliott and McCullough model]] |
| − | In [[Aufgaben: | + | In [[Aufgaben:Exercise_5.6:_Error_Correlation_Duration| "Exercise 5.6"]] and [[Aufgaben:Exercise_5.6Z:_Gilbert-Elliott_Model| "Exercise 5.6Z"]] the GE model with the parameter values |
:$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, | :$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, | ||
| − | \hspace{0.2cm}p_{\rm B} = 0.1, | + | \hspace{0.2cm}p_{\rm B} = 0.1,\hspace{0.2cm} |
| − | + | {\rm Pr}(\rm | |
G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ | G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ | ||
\hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm | \hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm | ||
B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$ | B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$ | ||
| − | + | are examined in more detail. Compared to these exercises, the transition probabilities are now renamed, for example $p(\rm B\hspace{0.05cm}|\hspace{0.05cm}G)$ is written instead of $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G)$. In the upper graph this renaming is already done. | |
| − | + | The lower graphic shows the MC model of McCullough. This has exactly the same structure as the GE model, but now all probabilities are denoted by $q$ instead of $p$. | |
| − | + | For example, in the MC model $q\rm (B\hspace{0.05cm}|\hspace{0.05cm}G)$ denotes the transition probability from state $\rm G$ to state $\rm B$ under the assumption that an error has just occurred in state $\rm G$. In contrast, the GE parameter $p \rm (B\hspace{0.05cm}|\hspace{0.05cm}G)$ denotes this transition probability without any additional condition. | |
| − | + | ||
| + | The parameters of the GE model ⇒ $p_{\rm G}, \hspace{0.1cm} p_{\rm B}, \hspace{0.1cm} p({\rm B\hspace{0.05cm}|\hspace{0.05cm}G}), \hspace{0.1cm} p({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})$ can be converted to the corresponding MC parameters $q_{\rm G}, \hspace{0.1cm} q_{\rm B},\hspace{0.1cm} q({\rm B\hspace{0.05cm}|\hspace{0.05cm}G})$ and $q({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})$ in such a way that an error sequence identical in its statistical properties to the GE model is produced, but not the identical sequence. | ||
| + | |||
| + | The conversion equations are: | ||
:$$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1-\beta_{\rm | :$$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1-\beta_{\rm | ||
G}\hspace{0.05cm}, \hspace{0.2cm}q_{\rm | G}\hspace{0.05cm}, \hspace{0.2cm}q_{\rm | ||
| − | B} = 1-\beta_{\rm B}\hspace{0.05cm}, | + | B} = 1-\beta_{\rm B}\hspace{0.05cm},\hspace{0.5cm} |
| − | + | q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \hspace{-0.1cm} \ = \ | |
| − | \hspace{-0.1cm}\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm | + | \hspace{-0.1cm}\frac{\alpha_{\rm B} \cdot \big [{\rm Pr}(\rm |
| − | B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}( | + | B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}( |
| − | G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot | + | G\hspace{0.05cm}|\hspace{0.05cm} B )\big ]}{\alpha_{\rm G} \cdot {\it q}_{\rm |
| − | B} + \alpha_{\rm B} \cdot | + | B} + \alpha_{\rm B} \cdot {\it q}_{\rm G}} \hspace{0.05cm},\hspace{0.5cm} |
| − | + | \hspace{0.2cm}{\it q}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )\hspace{-0.1cm} \ = \ | |
\hspace{-0.1cm} | \hspace{-0.1cm} | ||
| − | \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm | + | \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot {\it q}(\rm |
B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$ | B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$ | ||
| − | + | Here, the following auxiliary quantities are used: | |
:$$u_{\rm GG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm | :$$u_{\rm GG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm | ||
G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) | G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) | ||
| Line 59: | Line 62: | ||
\hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.$$ | \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.$$ | ||
| − | $w_{\rm G}$ | + | $w_{\rm G}$ and $w_{\rm B}$ are the state probabilities for "GOOD" and "BAD" of the GE model. In [[Aufgaben:Exercise_5.6Z:_Gilbert-Elliott_Model| "Exercise 5.6Z"]], these were calculated as follows: |
:$$w_{\rm G} = {10}/{11}\hspace{0.05cm}, \hspace{0.2cm}w_{\rm B} | :$$w_{\rm G} = {10}/{11}\hspace{0.05cm}, \hspace{0.2cm}w_{\rm B} | ||
= {1}/{11}\hspace{0.05cm}.$$ | = {1}/{11}\hspace{0.05cm}.$$ | ||
| − | + | The corresponding state probabilities of the MC model are $\alpha_{\rm G}$ and $\alpha_{\rm B}$. | |
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Notes:'' | |
| + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Burst_Error_Channels| "Burst Error Channels"]]. | ||
| + | * In the following [[Aufgaben:Exercise_5.7Z:_McCullough_Model_once_more|"Exercise 5.7Z"]] the most important descriptive quantities are calculated directly from the MC parameters: | ||
| + | ** Error correlation function, | ||
| + | ** correlation duration, | ||
| + | ** mean error probability and | ||
| + | ** error distance distribution | ||
| − | === | + | |
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the following auxiliary variables: |
| − | |type=" | + | |type="{}"} |
| − | + | $u_{\rm GG}\hspace{0.05cm} = \ $ { 0.98901 3% } | |
| − | + | $u_{\rm BG}\ = \ $ { 0.09 3% } | |
| + | $u_{\rm GB}\ = \ $ { 0.00999 3% } | ||
| + | $u_{\rm BB}\ = \ $ { 0.81 3% } | ||
| + | $\beta_{\rm G}\hspace{0.3cm} = \ $ { 0.9939 3% } | ||
| + | $\beta_{\rm B}\hspace{0.32cm} = \ $ { 0.8051 3% } | ||
| − | { | + | {What are the two error probabilities of the MC model? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $q_{\rm G} \hspace{0.08cm} = \ $ { 0.0061 3% } |
| + | $q_{\rm B} \ = \ $ { 0.1949 3% } | ||
| + | |||
| + | {Calculate the other auxiliary quantities: | ||
| + | |type="{}"} | ||
| + | $x_{\rm G} \ = \ $ { 0.5432 3% } | ||
| + | $x_{\rm B} \ = \ $ { -20.99964--19.77636 } | ||
| + | $\alpha_{\rm G} \hspace{0.05cm} = \ $ { 0.5975 3% } | ||
| + | $\alpha_{\rm B} \ = \ $ { 0.4025 3% } | ||
| + | |||
| + | {Calculate the transition probabilities of the MC model: | ||
| + | |type="{}"} | ||
| + | $q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)\ = \ $ { 0.3724 3% } | ||
| + | $q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\ = \ $ { 0.5528 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the $u$ auxiliary variables: |
| − | '''(2)''' | + | :$$u_{\rm GG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm |
| − | '''( | + | G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) = 0.99 |
| − | '''( | + | \cdot (1 -0.001) \hspace{0.15cm}\underline {\approx 0.98901} \hspace{0.05cm},$$ |
| − | '''( | + | :$$u_{\rm BG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm |
| + | G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\rm B})= 0.1 | ||
| + | \cdot (1 -0.1) \hspace{0.15cm}\underline {\approx 0.09} | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$u_{\rm GB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G})= 0.01 | ||
| + | \cdot (1 -0.001) \hspace{0.15cm}\underline {\approx 0.00999} \hspace{0.05cm},$$ | ||
| + | :$$u_{\rm BB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\rm B})= 0.9 | ||
| + | \cdot (1 -0.1) \hspace{0.15cm}\underline {\approx 0.81}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *It follows for the $\beta$ auxiliary quantities: | ||
| + | :$$\beta_{\rm G} =\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - | ||
| + | u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} | ||
| + | =\frac{0.98901 + 0.81 + | ||
| + | \sqrt{(0.98901 - 0.81)^2 + 4 \cdot 0.00999\cdot 0.09}}{2} | ||
| + | $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}\beta_{\rm G}= \frac{1.79901 + \sqrt{0.03204 | ||
| + | + 0.003596}}{2} = \frac{1.79901 + 0.18877}{2} \hspace{0.15cm}\underline {= 0.9939} | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$\beta_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm | ||
| + | GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot | ||
| + | u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}, = \ \hspace{-0.1cm}\text{...} = \frac{1.79901 - 0.18877}{2} | ||
| + | \hspace{0.15cm}\underline {= 0.8051} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Using the result of subtask '''(1)''', we obtain: | ||
| + | :$$q_{\rm G} = 1-\beta_{\rm G} = | ||
| + | 1 - 0.9939 \hspace{0.15cm}\underline {= 0.0061}\hspace{0.05cm}, \hspace{0.3cm}q_{\rm B} = 1-\beta_{\rm B}= 1 - 0.8051 \hspace{0.15cm}\underline {= | ||
| + | 0.1949}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' According to the data section, the following is to be applied here | ||
| + | :$$x_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm | ||
| + | BG}}{\beta_{\rm G}-u_{\rm BB}}= | ||
| + | \frac{0.0999}{0.9939-0.81}\hspace{0.15cm}\underline {= 0.5432}\hspace{0.05cm},$$ | ||
| + | :$$ x_{\rm B} \hspace{-0.1cm} \ = \ | ||
| + | \hspace{-0.1cm}\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}= | ||
| + | \frac{0.0999}{0.8051-0.81}\hspace{0.15cm}\underline {= -20.388}\hspace{0.05cm},$$ | ||
| + | :$$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{(w_{\rm | ||
| + | G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( | ||
| + | x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} = \frac{(0.9091 \cdot 0.001 + | ||
| + | 0.0909 \cdot 0.1\cdot 0.5432)( -20.388-1)}{0.01 \cdot( -20.388 | ||
| + | -0.5432)} \hspace{0.15cm}\underline {= 0.5975} \hspace{0.05cm},$$ | ||
| + | :$$\alpha_{\rm B} | ||
| + | \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1-\alpha_{\rm G} \hspace{0.15cm}\underline {= | ||
| + | 0.4025}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' According to the given equations: | ||
| + | :$$q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \hspace{-0.1cm} \ = \ | ||
| + | \hspace{-0.1cm}\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm | ||
| + | G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm | ||
| + | B} + \alpha_{\rm B} \cdot q_{\rm G}} =\frac{0.4025 \cdot[0.1 + | ||
| + | 0.01]}{0.5975 \cdot 0.1949 + 0.4025 \cdot 0.0061}\hspace{0.15cm}\underline {= 0.3724} | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \hspace{-0.1cm} \ = \ | ||
| + | \hspace{-0.1cm} \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm | ||
| + | B\hspace{0.05cm}|\hspace{0.05cm} G )= \frac{0.5975}{0.4025} \cdot | ||
| + | 0.3724 \hspace{0.15cm}\underline {= 0.5528}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^5.3 Burst Error Channels^]] |
Latest revision as of 14:25, 19 October 2022
In "Exercise 5.6" and "Exercise 5.6Z" the GE model with the parameter values
- $$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,\hspace{0.2cm} {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
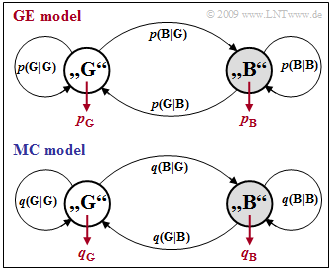
are examined in more detail. Compared to these exercises, the transition probabilities are now renamed, for example $p(\rm B\hspace{0.05cm}|\hspace{0.05cm}G)$ is written instead of $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G)$. In the upper graph this renaming is already done.
The lower graphic shows the MC model of McCullough. This has exactly the same structure as the GE model, but now all probabilities are denoted by $q$ instead of $p$.
For example, in the MC model $q\rm (B\hspace{0.05cm}|\hspace{0.05cm}G)$ denotes the transition probability from state $\rm G$ to state $\rm B$ under the assumption that an error has just occurred in state $\rm G$. In contrast, the GE parameter $p \rm (B\hspace{0.05cm}|\hspace{0.05cm}G)$ denotes this transition probability without any additional condition.
The parameters of the GE model ⇒ $p_{\rm G}, \hspace{0.1cm} p_{\rm B}, \hspace{0.1cm} p({\rm B\hspace{0.05cm}|\hspace{0.05cm}G}), \hspace{0.1cm} p({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})$ can be converted to the corresponding MC parameters $q_{\rm G}, \hspace{0.1cm} q_{\rm B},\hspace{0.1cm} q({\rm B\hspace{0.05cm}|\hspace{0.05cm}G})$ and $q({\rm G\hspace{0.05cm}|\hspace{0.05cm}B})$ in such a way that an error sequence identical in its statistical properties to the GE model is produced, but not the identical sequence.
The conversion equations are:
- $$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1-\beta_{\rm G}\hspace{0.05cm}, \hspace{0.2cm}q_{\rm B} = 1-\beta_{\rm B}\hspace{0.05cm},\hspace{0.5cm} q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{\alpha_{\rm B} \cdot \big [{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}( G\hspace{0.05cm}|\hspace{0.05cm} B )\big ]}{\alpha_{\rm G} \cdot {\it q}_{\rm B} + \alpha_{\rm B} \cdot {\it q}_{\rm G}} \hspace{0.05cm},\hspace{0.5cm} \hspace{0.2cm}{\it q}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot {\it q}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$
Here, the following auxiliary quantities are used:
- $$u_{\rm GG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},$$
- $$u_{\rm BB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} \beta_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm},$$
- $$\beta_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm},$$
- $$x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}$$
- $$\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.$$
$w_{\rm G}$ and $w_{\rm B}$ are the state probabilities for "GOOD" and "BAD" of the GE model. In "Exercise 5.6Z", these were calculated as follows:
- $$w_{\rm G} = {10}/{11}\hspace{0.05cm}, \hspace{0.2cm}w_{\rm B} = {1}/{11}\hspace{0.05cm}.$$
The corresponding state probabilities of the MC model are $\alpha_{\rm G}$ and $\alpha_{\rm B}$.
Notes:
- The exercise belongs to the chapter "Burst Error Channels".
- In the following "Exercise 5.7Z" the most important descriptive quantities are calculated directly from the MC parameters:
- Error correlation function,
- correlation duration,
- mean error probability and
- error distance distribution
Questions
Solution
- $$u_{\rm GG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) = 0.99 \cdot (1 -0.001) \hspace{0.15cm}\underline {\approx 0.98901} \hspace{0.05cm},$$
- $$u_{\rm BG} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\rm B})= 0.1 \cdot (1 -0.1) \hspace{0.15cm}\underline {\approx 0.09} \hspace{0.05cm},$$
- $$u_{\rm GB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G})= 0.01 \cdot (1 -0.001) \hspace{0.15cm}\underline {\approx 0.00999} \hspace{0.05cm},$$
- $$u_{\rm BB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\rm B})= 0.9 \cdot (1 -0.1) \hspace{0.15cm}\underline {\approx 0.81}\hspace{0.05cm}.$$
- It follows for the $\beta$ auxiliary quantities:
- $$\beta_{\rm G} =\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} =\frac{0.98901 + 0.81 + \sqrt{(0.98901 - 0.81)^2 + 4 \cdot 0.00999\cdot 0.09}}{2} $$
- $$\Rightarrow \hspace{0.3cm}\beta_{\rm G}= \frac{1.79901 + \sqrt{0.03204 + 0.003596}}{2} = \frac{1.79901 + 0.18877}{2} \hspace{0.15cm}\underline {= 0.9939} \hspace{0.05cm},$$
- $$\beta_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}, = \ \hspace{-0.1cm}\text{...} = \frac{1.79901 - 0.18877}{2} \hspace{0.15cm}\underline {= 0.8051} \hspace{0.05cm}.$$
(2) Using the result of subtask (1), we obtain:
- $$q_{\rm G} = 1-\beta_{\rm G} = 1 - 0.9939 \hspace{0.15cm}\underline {= 0.0061}\hspace{0.05cm}, \hspace{0.3cm}q_{\rm B} = 1-\beta_{\rm B}= 1 - 0.8051 \hspace{0.15cm}\underline {= 0.1949}\hspace{0.05cm}.$$
(3) According to the data section, the following is to be applied here
- $$x_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}}= \frac{0.0999}{0.9939-0.81}\hspace{0.15cm}\underline {= 0.5432}\hspace{0.05cm},$$
- $$ x_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}= \frac{0.0999}{0.8051-0.81}\hspace{0.15cm}\underline {= -20.388}\hspace{0.05cm},$$
- $$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} = \frac{(0.9091 \cdot 0.001 + 0.0909 \cdot 0.1\cdot 0.5432)( -20.388-1)}{0.01 \cdot( -20.388 -0.5432)} \hspace{0.15cm}\underline {= 0.5975} \hspace{0.05cm},$$
- $$\alpha_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1-\alpha_{\rm G} \hspace{0.15cm}\underline {= 0.4025}\hspace{0.05cm}.$$
(4) According to the given equations:
- $$q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} =\frac{0.4025 \cdot[0.1 + 0.01]}{0.5975 \cdot 0.1949 + 0.4025 \cdot 0.0061}\hspace{0.15cm}\underline {= 0.3724} \hspace{0.05cm},$$
- $$q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )= \frac{0.5975}{0.4025} \cdot 0.3724 \hspace{0.15cm}\underline {= 0.5528}\hspace{0.05cm}.$$