Difference between revisions of "Aufgaben:Exercise 5.7: Rectangular Matched Filter"
m (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| (13 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Matched_Filter |
}} | }} | ||
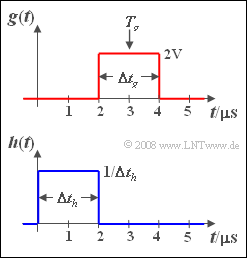
| − | [[File:P_ID574__Sto_A_5_7.png|right| | + | [[File:P_ID574__Sto_A_5_7.png|right|frame|Pulse $g(t)$ and Matched Filter impulse response $h(t)$]] |
| − | + | At the input of a lowpass filter with a rectangular impulse response $h(t)$ the reception signal $r(t)$ is present, which is additively composed of a pulse-shaped signal component $g(t)$ and a noise component $n(t)$. It holds: | |
| − | * | + | * The pulse $g(t)$ is rectangular. |
| − | * | + | * The pulse duration is $\Delta t_g = 2 \hspace{0.08cm}\rm µ s$. |
| − | * | + | * The pulse amplitude is $g_0 = 2 \hspace{0.08cm}\rm V$. |
| − | * | + | * The center of the pulse is at $T_g = 3 \hspace{0.08cm}\rm µ s$. |
| − | * | + | * The noise $n(t)$ is white and Gaussian distributed. |
| − | * | + | * The power density is $N_0 = 4 \cdot 10^{-6} \hspace{0.08cm}\rm V^2\hspace{-0.1cm}/Hz$ with respect to the $1 \hspace{0.08cm}\rm \Omega$ resistor. |
| − | + | The rectangular impulse response of the filter starts at $t = 0$. | |
| + | *The impulse response duration $\Delta t_h$ is freely selectable. | ||
| + | *The height $1/\Delta t_h$ of the impulse response is adjusted in each case so that $H(f = 0) = 1$. | ||
| − | + | ||
| − | * | + | |
| − | * | + | Notes: |
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Matched_Filter|Matched Filter]]. | ||
| + | *For the questions '''(1)''' to '''(6)''': $\Delta t_h =\Delta t_g = 2 \hspace{0.05cm}\rm µ s$ always applies. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the statements are true under the assumption $\Delta t_h =\Delta t_g$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The filter is matched to the input pulse $g(t)$. |
| − | - | + | - There is another filter with larger S/N ratio. |
| − | + | + | + The filter can be implemented as an integrator over time $\Delta t_h$. |
| − | { | + | {What is the optimal detection time? |
|type="{}"} | |type="{}"} | ||
| − | $T_\text{D, opt} \ = $ { 4 3% } $\ \rm | + | $T_\text{D, opt} \ = \ $ { 4 3% } $\ \rm µ s$ |
| − | { | + | {What is the value of the matched filter constant here? |
|type="{}"} | |type="{}"} | ||
| − | $K_\text{MF} \ = $ { 0.25 3% } $\cdot 10^6 \ \rm 1/Vs$ | + | $K_\text{MF} \ = \ $ { 0.25 3% } $\cdot 10^6 \ \rm 1/Vs$ |
| − | { | + | {What is the S/N ratio at the optimal detection time? |
|type="{}"} | |type="{}"} | ||
| − | $\rho_d(T_\text{D, opt}) \ = $ { 4 3% } | + | $\rho_d(T_\text{D, opt}) \ = \ $ { 4 3% } |
| − | { | + | {What is the value of the signal component $d_{\rm S}(t)$ at the optimal time $T_\text{D, opt}$ and the noise power $\sigma_d^2$ in front of the detector? |
|type="{}"} | |type="{}"} | ||
| − | $d_{\rm S}(T_\text{D, opt}) \ = $ { 2 3% } $\ \rm V$ | + | $d_{\rm S}(T_\text{D, opt}) \ = \ $ { 2 3% } $\ \rm V$ |
| − | $\sigma_d^2 \ = $ { 1 3% } $\ \rm V^2$ | + | $\sigma_d^2 \ = \ $ { 1 3% } $\ \rm V^2$ |
| − | { | + | {What is the S/N ratio at the detection time $T_{\rm D} = 3 \hspace{0.08cm}\rm µ s$? |
|type="{}"} | |type="{}"} | ||
| − | $\rho_d(T_{\rm D} = 3 \hspace{0. | + | $\rho_d(T_{\rm D} = 3 \hspace{0.08cm}\rm µ s) \ = \ $ { 1 3% } |
| − | { | + | {Which of the following statements are true if $\Delta t_h =1 \hspace{0.08cm}\rm µ s$ holds? Note: In the range from $0$ to $1 \hspace{0.05cm}\rm µ s$, the impulse response thus has the value $10^6 \ \rm 1/s$. |
| − | |||
|type="[]"} | |type="[]"} | ||
| − | + | + | + Each time point $T_{\rm D}$ in the range $3 \hspace{0.08cm}\rm µ s$ ... $4 \hspace{0.05cm}\rm µ s$ leads to the maximum SNR. |
| − | - | + | - The signal component $d_S(T_\text{D, opt})$ is smaller than calculated in subtask '''(5)'''. |
| − | + | + | + The noise power $\sigma_d^2$ is larger than calculated in subtask '''(5)'''. |
| − | + | + | + The S/N ratio is smaller than calculated in subtask '''(4)'''. |
| − | { | + | {Which of the following statements are true if $\Delta t_h =3 \hspace{0.08cm}\rm µ s$? Note: In the range from $0$ to $3 \hspace{0.05cm}\rm µ s$ the impulse response has the value $0.33 \cdot 10^6 \ \rm 1/s$. |
| − | |||
|type="[]"} | |type="[]"} | ||
| − | - | + | - Each time point $T_{\rm D}$ in the range $3 \hspace{0.08cm}\rm µ s$ ... $4 \hspace{0.05cm}\rm µ s$ leads to the maximum SNR. |
| − | + | + | + The signal component $d_S(T_\text{D, opt})$ is smaller than calculated in subtask '''(5)'''. |
| − | - | + | - The noise power $\sigma_d^2$ is larger than calculated in subtask '''(5)'''. |
| − | + | + | + The S/N ratio is smaller than calculated in subtask '''(4)'''. |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solutions 1 and 3</u> are correct: |
| − | * | + | *For the same pulse duration $(\Delta t_h =\Delta t_g)$, there is a matched filter, even if $g(t)$ and $h(t)$ differ in amplitude and temporal position. |
| − | * | + | *Thus, there is no other filter with better signal–to–noise power ratio. |
| − | * | + | *The filter with rectangular impulse response can also be interpreted as an integrator over the time duration $\Delta t_h$. |
| − | |||
| − | |||
| − | |||
| + | '''(2)''' The impulse response of the matched filter is: $h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$ | ||
| + | *The input impulse $g(t)$ is non-zero in the range from $2 \hspace{0.05cm}\rm µ s$ to $4 \hspace{0.08cm}\rm µ s$, and in the range from $-4 \hspace{0.08cm}\rm µ s$ to $-2 \hspace{0.08cm}\rm µ s$, when mirrored. | ||
| + | *After shifting by $4 \hspace{0.08cm}\rm µ s$, it is achieved that $g(T_{\rm D} - t)$ is, like the impulse response $h(t)$, between $0$ and $2 \hspace{0.08cm}\rm µ s$. | ||
| + | *From this follows: $T_\text{D, opt}\hspace{0.15cm}\underline{ =4 \hspace{0.08cm}\rm µ s}$. | ||
| − | |||
| − | '''( | + | '''(3)''' With $\Delta t_h =\Delta t_g = 2 \cdot 10^{-6}\hspace{0.05cm}\rm µ s$ and $g_0 = 2 \hspace{0.08cm}\rm V$, we obtain $K_{\rm MF} = 1/(\Delta t_g \cdot g_0)\hspace{0.15cm}\underline{ =0.25 \cdot 10^{6}\hspace{0.08cm}\rm (1/Vs)}$. |
| − | |||
| − | [[File:P_ID575__Sto_A_5_7_f.png|right| | + | |
| − | '''(5)''' | + | |
| + | '''(4)''' The energy of the pulse $g(t)$ is $E_g = g_0^2 \cdot \Delta t_g = 8 \cdot 10^{-6}\hspace{0.05cm}\rm V^2s$. | ||
| + | *From this it follows for the maximum S/N ratio: | ||
| + | :$$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{2 \cdot E_g }{N_0 } = \frac{{2 \cdot 8 \cdot 10^{ - 6} \;{\rm{V}}^2 {\rm{s}}}}{{4 \cdot 10^{ - 6} \;{\rm{V}}^2 /{\rm{Hz}}}}\hspace{0.15cm}\underline{ = 4}.$$ | ||
| + | |||
| + | |||
| + | |||
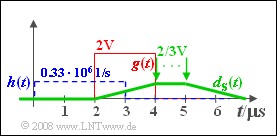
| + | [[File:P_ID575__Sto_A_5_7_f.png|right|frame|MF output $d_{\rm S}(t)$ for subtask '''(5)''']] | ||
| + | '''(5)''' The matched filter output pulse $d_{\rm S}(t)$ is triangular between $2 \hspace{0.05cm}\rm µ s$ and $6 \hspace{0.05cm}\rm µ s$. | ||
| + | *The maximum $g_0\hspace{0.15cm}\underline{= 2 \hspace{0.08cm}\rm V}$ is at $T_\text{D, opt} =4 \hspace{0.05cm}\rm µ s$. | ||
| + | *The noise power is given by: | ||
:$$\sigma _d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } \hspace{0.15 cm}\underline{= 1\;{\rm{V}}^2} .$$ | :$$\sigma _d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } \hspace{0.15 cm}\underline{= 1\;{\rm{V}}^2} .$$ | ||
| − | + | *Using these two quantities, we can calculate the maximum S/N ratio: | |
| − | :$$\rho _d (T_{{\rm{D, \hspace{0. | + | :$$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{{d_{\rm S} (T_{{\rm{D, \hspace{0.05cm}opt}}} )^2}}{\sigma _d ^2 } = \frac{({2\;{\rm{V}})^2 }}{{1\;{\rm{V}}^2 }} = 4.$$ |
| + | |||
| + | |||
| + | '''(6)''' From the above diagram, one can see that now $d_{\rm S}(T_\text{D})$ is only half as large, namely $1 \hspace{0.08cm}\rm V$. | ||
| + | *Thus for $T_\text{D} =3 \hspace{0.08cm}\rm µ s$ the S/N ratio is smaller by a factor of $4$, i.e. $\rho _d (T_{{\rm{D}}} )\hspace{0.15 cm}\underline{=1}$. | ||
| + | |||
| − | |||
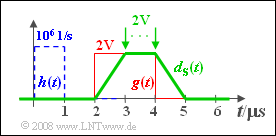
| − | [[File:P_ID576__Sto_A_5_7_g.png|right| | + | [[File:P_ID576__Sto_A_5_7_g.png|right|frame|MF output $d_{\rm S}(t)$ for subtask '''(7)''']] |
| − | '''(7)''' | + | '''(7)''' <u>Solutions 1, 3 and 4</u> are correct: |
| − | * | + | *The diagram shows that now the output pulse $d_{\rm S}(t)$ is trapezoidal. |
| − | * | + | *In the range from $3 \hspace{0.05cm}\rm µ s$ to $4 \hspace{0.05cm}\rm µ s$ the pulse $d_{\rm S}(t)$ is constantly equal to $g_0= 2 \hspace{0.08cm}\rm V$. |
| − | * | + | *Because of the only half as wide impulse response $h(t)$, the frequency response $H(f)$ is more broadband by a factor of $2$ and thus the noise power is larger: |
:$$\sigma_d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {h^2 (t)\,{\rm{d}}t} = \frac{N_0 }{2 \cdot \Delta t_h } = 2\;{\rm{V}}^2 .$$ | :$$\sigma_d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {h^2 (t)\,{\rm{d}}t} = \frac{N_0 }{2 \cdot \Delta t_h } = 2\;{\rm{V}}^2 .$$ | ||
| − | * | + | *Thus, the S/N ratio is now $\rho_d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) \hspace{0.15cm}\underline{= 2}.$ |
| + | |||
| + | |||
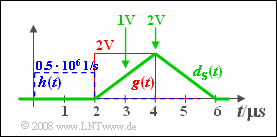
| − | [[File:P_ID577__Sto_A_5_7_h.png|right| | + | [[File:P_ID577__Sto_A_5_7_h.png|right|frame|MF output $d_{\rm S}(t)$ for subtask '''(8)''']] |
| − | '''(8)''' | + | '''(8)''' <u>Solutions 2 and 4</u> are correct: |
| − | * | + | *The matched filter output pulse $d_{\rm S}(t)$ for $\Delta t_h = 3 \hspace{0.05cm}\rm µ s$ is sketched on the right. This is also trapezoidal. |
| − | * | + | *The optimal detection time is now in the range between $4 \hspace{0.05cm}\rm µ s$ and $5 \hspace{0.05cm}\rm µ s$. |
| − | * | + | *However, the useful signal $d_{\rm S}(t)$ is now only one-third as large as when matched: $d_{\rm S}(T_\text{D, opt}) = 2/3 \hspace{0.08cm}\rm V$. |
| − | * | + | *For the noise power now applies: |
:$$\sigma_d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } = \frac{2}{3}\;{\rm{V}}^2 .$$ | :$$\sigma_d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } = \frac{2}{3}\;{\rm{V}}^2 .$$ | ||
| − | * | + | *Thus, the noise power is smaller (i.e. more favorable) than with adaptation according to subtask '''(5)'''. |
| − | * | + | *Nevertheless, the S/N ratio is still worse than in subtask '''(7)''' due to the smaller $d_{\rm S}(T_{\rm D})$: |
| − | :$$\rho _d (T_{{\rm{D\hspace{0. | + | :$$\rho _d (T_{{\rm{D\hspace{0.15cm},opt}}} ) = \frac{{(2/3\;{\rm{V}})^2 }}{{2/3\;{\rm{V}}^2 }} = {2}/{3}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 130: | Line 146: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^5.4 Matched Filter^]] |
Latest revision as of 15:21, 21 February 2022
At the input of a lowpass filter with a rectangular impulse response $h(t)$ the reception signal $r(t)$ is present, which is additively composed of a pulse-shaped signal component $g(t)$ and a noise component $n(t)$. It holds:
- The pulse $g(t)$ is rectangular.
- The pulse duration is $\Delta t_g = 2 \hspace{0.08cm}\rm µ s$.
- The pulse amplitude is $g_0 = 2 \hspace{0.08cm}\rm V$.
- The center of the pulse is at $T_g = 3 \hspace{0.08cm}\rm µ s$.
- The noise $n(t)$ is white and Gaussian distributed.
- The power density is $N_0 = 4 \cdot 10^{-6} \hspace{0.08cm}\rm V^2\hspace{-0.1cm}/Hz$ with respect to the $1 \hspace{0.08cm}\rm \Omega$ resistor.
The rectangular impulse response of the filter starts at $t = 0$.
- The impulse response duration $\Delta t_h$ is freely selectable.
- The height $1/\Delta t_h$ of the impulse response is adjusted in each case so that $H(f = 0) = 1$.
Notes:
- The exercise belongs to the chapter Matched Filter.
- For the questions (1) to (6): $\Delta t_h =\Delta t_g = 2 \hspace{0.05cm}\rm µ s$ always applies.
Questions
Solution
- For the same pulse duration $(\Delta t_h =\Delta t_g)$, there is a matched filter, even if $g(t)$ and $h(t)$ differ in amplitude and temporal position.
- Thus, there is no other filter with better signal–to–noise power ratio.
- The filter with rectangular impulse response can also be interpreted as an integrator over the time duration $\Delta t_h$.
(2) The impulse response of the matched filter is: $h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$
- The input impulse $g(t)$ is non-zero in the range from $2 \hspace{0.05cm}\rm µ s$ to $4 \hspace{0.08cm}\rm µ s$, and in the range from $-4 \hspace{0.08cm}\rm µ s$ to $-2 \hspace{0.08cm}\rm µ s$, when mirrored.
- After shifting by $4 \hspace{0.08cm}\rm µ s$, it is achieved that $g(T_{\rm D} - t)$ is, like the impulse response $h(t)$, between $0$ and $2 \hspace{0.08cm}\rm µ s$.
- From this follows: $T_\text{D, opt}\hspace{0.15cm}\underline{ =4 \hspace{0.08cm}\rm µ s}$.
(3) With $\Delta t_h =\Delta t_g = 2 \cdot 10^{-6}\hspace{0.05cm}\rm µ s$ and $g_0 = 2 \hspace{0.08cm}\rm V$, we obtain $K_{\rm MF} = 1/(\Delta t_g \cdot g_0)\hspace{0.15cm}\underline{ =0.25 \cdot 10^{6}\hspace{0.08cm}\rm (1/Vs)}$.
(4) The energy of the pulse $g(t)$ is $E_g = g_0^2 \cdot \Delta t_g = 8 \cdot 10^{-6}\hspace{0.05cm}\rm V^2s$.
- From this it follows for the maximum S/N ratio:
- $$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{2 \cdot E_g }{N_0 } = \frac{{2 \cdot 8 \cdot 10^{ - 6} \;{\rm{V}}^2 {\rm{s}}}}{{4 \cdot 10^{ - 6} \;{\rm{V}}^2 /{\rm{Hz}}}}\hspace{0.15cm}\underline{ = 4}.$$
(5) The matched filter output pulse $d_{\rm S}(t)$ is triangular between $2 \hspace{0.05cm}\rm µ s$ and $6 \hspace{0.05cm}\rm µ s$.
- The maximum $g_0\hspace{0.15cm}\underline{= 2 \hspace{0.08cm}\rm V}$ is at $T_\text{D, opt} =4 \hspace{0.05cm}\rm µ s$.
- The noise power is given by:
- $$\sigma _d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } \hspace{0.15 cm}\underline{= 1\;{\rm{V}}^2} .$$
- Using these two quantities, we can calculate the maximum S/N ratio:
- $$\rho _d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) = \frac{{d_{\rm S} (T_{{\rm{D, \hspace{0.05cm}opt}}} )^2}}{\sigma _d ^2 } = \frac{({2\;{\rm{V}})^2 }}{{1\;{\rm{V}}^2 }} = 4.$$
(6) From the above diagram, one can see that now $d_{\rm S}(T_\text{D})$ is only half as large, namely $1 \hspace{0.08cm}\rm V$.
- Thus for $T_\text{D} =3 \hspace{0.08cm}\rm µ s$ the S/N ratio is smaller by a factor of $4$, i.e. $\rho _d (T_{{\rm{D}}} )\hspace{0.15 cm}\underline{=1}$.
(7) Solutions 1, 3 and 4 are correct:
- The diagram shows that now the output pulse $d_{\rm S}(t)$ is trapezoidal.
- In the range from $3 \hspace{0.05cm}\rm µ s$ to $4 \hspace{0.05cm}\rm µ s$ the pulse $d_{\rm S}(t)$ is constantly equal to $g_0= 2 \hspace{0.08cm}\rm V$.
- Because of the only half as wide impulse response $h(t)$, the frequency response $H(f)$ is more broadband by a factor of $2$ and thus the noise power is larger:
- $$\sigma_d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {h^2 (t)\,{\rm{d}}t} = \frac{N_0 }{2 \cdot \Delta t_h } = 2\;{\rm{V}}^2 .$$
- Thus, the S/N ratio is now $\rho_d (T_{{\rm{D, \hspace{0.08cm}opt}}} ) \hspace{0.15cm}\underline{= 2}.$
(8) Solutions 2 and 4 are correct:
- The matched filter output pulse $d_{\rm S}(t)$ for $\Delta t_h = 3 \hspace{0.05cm}\rm µ s$ is sketched on the right. This is also trapezoidal.
- The optimal detection time is now in the range between $4 \hspace{0.05cm}\rm µ s$ and $5 \hspace{0.05cm}\rm µ s$.
- However, the useful signal $d_{\rm S}(t)$ is now only one-third as large as when matched: $d_{\rm S}(T_\text{D, opt}) = 2/3 \hspace{0.08cm}\rm V$.
- For the noise power now applies:
- $$\sigma_d ^2 = \frac{N_0 }{2 \cdot \Delta t_h } = \frac{2}{3}\;{\rm{V}}^2 .$$
- Thus, the noise power is smaller (i.e. more favorable) than with adaptation according to subtask (5).
- Nevertheless, the S/N ratio is still worse than in subtask (7) due to the smaller $d_{\rm S}(T_{\rm D})$:
- $$\rho _d (T_{{\rm{D\hspace{0.15cm},opt}}} ) = \frac{{(2/3\;{\rm{V}})^2 }}{{2/3\;{\rm{V}}^2 }} = {2}/{3}.$$