Difference between revisions of "Aufgaben:Exercise 5.8Z: Matched Filter for Rectangular PSD"
From LNTwww
m (Text replacement - "power spectral density" to "power-spectral density") |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
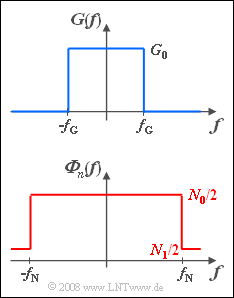
| − | [[File:P_ID647__Sto_Z_5_8.png|right|frame| | + | [[File:P_ID647__Sto_Z_5_8.png|right|frame|Spectrum $G(f)\ \bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \ g(t)$; <br>power-sprectral density ${\it \Phi}_n (f)$]] |
| − | The interference power density effective on a system can be assumed to be constant in range: | + | The interference power-spectral density effective on a system can be assumed to be constant in range: |
| − | :$$\it{\Phi} _n \left( f \right) = \left\{ \begin{array}{l} N_0 /2 \\ N_1 /2 \\ \end{array} \right.\quad \begin{array}{*{20}c} \rm{ | + | :$$\it{\Phi} _n \left( f \right) = \left\{ \begin{array}{l} N_0 /2 \\ N_1 /2 \\ \end{array} \right.\quad \begin{array}{*{20}c} \rm{for} \\ \rm{for} \\\end{array}\quad \begin{array}{*{20}c} {\left| f \right| \le f_{\rm N} ,} \\ {\left| f \right| > f_{\rm N} .} \\\end{array}$$ |
| − | *Here, let the | + | *Here, let the power-spectral density $N_1$ in the outer region $|f| > f_{\rm N}$ always be much smaller than $N_0$. |
| − | *For example, use the following values: | + | *For example, use the following values: |
:$$N_0 = 2 \cdot 10^{ - 6} \;{\rm{V}}^{\rm{2}} /{\rm{Hz}},\quad N_1 = 2 \cdot 10^{ - 8} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$ | :$$N_0 = 2 \cdot 10^{ - 6} \;{\rm{V}}^{\rm{2}} /{\rm{Hz}},\quad N_1 = 2 \cdot 10^{ - 8} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$ | ||
| − | Such an interference signal $n(t)$ occurs, for example, when the dominant interference source contains only components below the frequency limit $f_{\rm N}$. Due to the unavoidable thermal noise, also for $|f| > f_{\rm N}$ | + | Such an interference signal $n(t)$ occurs, for example, when the dominant interference source contains only components below the frequency limit $f_{\rm N}$. Due to the unavoidable thermal noise, also for $|f| > f_{\rm N}$ interference power-spectral density is ${\it \Phi}_n(f) \ne 0$. |
| − | Further, it holds: | + | Further, it holds: |
| − | *Let the spectrum $G(f)$ of the useful signal also be rectangular according to the above diagram. | + | *Let the spectrum $G(f)$ of the useful signal $g(t)$ also be rectangular according to the above diagram. |
| − | *Therefore, | + | *Therefore, $g(t)$ has the following curve with $\Delta f = 2 \cdot f_{\rm G}$: |
| − | :$$g(t) = G_0 \cdot \Delta f \cdot {\mathop{\rm | + | :$$g(t) = G_0 \cdot \Delta f \cdot {\mathop{\rm sinc}\nolimits} \left( { \Delta f \cdot t} \right).$$ |
| − | *Let the | + | *Let the frequency response $H_{\rm E}(f)$ of the receiver filter (German: "Empfangsfilter" ⇒ subscript "E") be optimally matched to the spectrum $G(f)$ and the interference power-spectral density ${\it \Phi}_n(f)$. |
| − | *That is, let $H_{\rm E}(f) = H_{\rm MF}(f)$. Let the detection time be simplified $T_{\rm D} = 0$ (acausal system description). | + | *That is, let $H_{\rm E}(f) = H_{\rm MF}(f)$ ⇒ "Matched Filter". |
| + | *Let the detection time be simplified $T_{\rm D} = 0$ (acausal system description). | ||
| Line 28: | Line 29: | ||
| − | + | Notes: | |
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Matched_Filter|Matched Filter]]. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Matched_Filter|Matched Filter]]. | ||
| Line 41: | Line 42: | ||
{Which of the following statements are valid under the condition $f_{\rm N} > f_{\rm G}$? | {Which of the following statements are valid under the condition $f_{\rm N} > f_{\rm G}$? | ||
|type="[]"} | |type="[]"} | ||
| − | + Applicable is the "matched filter | + | + Applicable is the "matched filter for white noise". |
| − | - The | + | - The matched filter output pulse is triangular. |
| − | + The | + | + The matched filter output pulse is $\rm sinc$–shaped. |
| − | - The | + | - The matched filter output pulse is $\rm sinc^2$–shaped. |
| − | {What is the S/N ratio ( | + | {What is the S/N ratio (SNR) of the detection signal $d(t)$ for $f_{\rm N} > f_{\rm G}$? |
|type="{}"} | |type="{}"} | ||
$10 \cdot \lg \; \rho_d \ = \ $ { 20 3% } $\ \rm dB$ | $10 \cdot \lg \; \rho_d \ = \ $ { 20 3% } $\ \rm dB$ | ||
| − | {What SNR | + | {What SNR results for $f_{\rm N} = f_{\rm G}/2$? Interpretation. |
|type="{}"} | |type="{}"} | ||
$10 \cdot \lg \; \rho_d \ = \ $ { 37.03 3% } $\ \rm dB$ | $10 \cdot \lg \; \rho_d \ = \ $ { 37.03 3% } $\ \rm dB$ | ||
| Line 62: | Line 63: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u>Solutions 1 and 3</u> are correct: | + | '''(1)''' <u>Solutions 1 and 3</u> are correct: |
| − | *For all frequencies $|f| > f_{\rm G}$ at which the useful signal has spectral components $(G_d(f) \ne 0)$, the interference power-spectral density is ${\it}\Phi_n(f) = N_0/2$. | + | *For all frequencies $|f| > f_{\rm G}$ at which the useful signal $d_{\rm S}(t)$ has spectral components $(G_d(f) \ne 0)$, <br>the interference power-spectral density is ${\it}\Phi_n(f) = N_0/2$. |
| − | *Thus, the frequency response of the matched filter, assuming $T_{\rm D} = 0$ | + | *Thus, the frequency response of the matched filter is, assuming $T_{\rm D} = 0$: |
:$$H_{\rm MF} (f) = K_{\rm MF} \cdot G(f).$$ | :$$H_{\rm MF} (f) = K_{\rm MF} \cdot G(f).$$ | ||
| − | *In this case, the optimal frequency response $H_{\rm MF}(f)$, just like $G(f)$, is rectangular with width $\Delta f$. | + | *In this case, the optimal frequency response $H_{\rm MF}(f)$, just like $G(f)$, is rectangular with width $\Delta f$. |
| − | *Thus, for the useful component of the | + | *Thus, for the useful component of the matched filter output signal $d(t)$ holds: |
:$$d_{\rm S}(t)\quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \quad G(f) \cdot H_{\rm MF} (f).$$ | :$$d_{\rm S}(t)\quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \quad G(f) \cdot H_{\rm MF} (f).$$ | ||
*The product of two rectangular functions of equal width again yields a rectangular function. | *The product of two rectangular functions of equal width again yields a rectangular function. | ||
| − | *It further follows that the output pulse of the matched filter is also $\rm | + | *It further follows that the output pulse of the matched filter is also $\rm sinc$–shaped. |
| Line 79: | Line 80: | ||
*The integral yields the value $G_0^2 \cdot \Delta f$. It follows that: | *The integral yields the value $G_0^2 \cdot \Delta f$. It follows that: | ||
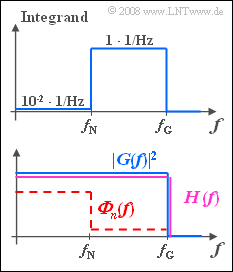
| + | [[File:P_ID648__Sto_Z_5_8_c.png|right|frame|Regarding subtask '''(3)''']] | ||
| + | |||
:$$\rho _d = \frac{G_0 ^2 \cdot \Delta f }{N_0 /2} = \frac{ 10^{ - 8}\,(\rm V/Hz)^2 \;\cdot10^4 \;{\rm{Hz}} }{10^{ - 6}\,\rm V^2/Hz} = 10^2 | :$$\rho _d = \frac{G_0 ^2 \cdot \Delta f }{N_0 /2} = \frac{ 10^{ - 8}\,(\rm V/Hz)^2 \;\cdot10^4 \;{\rm{Hz}} }{10^{ - 6}\,\rm V^2/Hz} = 10^2 | ||
\quad \Rightarrow \quad 10\lg \rho _d \hspace{0.15cm}\underline { = 20\;{\rm{dB}}}.$$ | \quad \Rightarrow \quad 10\lg \rho _d \hspace{0.15cm}\underline { = 20\;{\rm{dB}}}.$$ | ||
| − | + | '''(3)''' In general, the SNR for colored interference is: | |
| − | '''(3)''' In general, the SNR for colored interference is: | ||
:$$\rho _d = 2 \cdot \int_0^\infty \frac{\left| {G(f)} \right|^2 }{{\it \Phi}_n (f)} \, {\rm{d}}f.$$ | :$$\rho _d = 2 \cdot \int_0^\infty \frac{\left| {G(f)} \right|^2 }{{\it \Phi}_n (f)} \, {\rm{d}}f.$$ | ||
| − | *As can be seen from the accompanying qualitative diagram, the integrand is piecewise constant for the given frequency responses. | + | *As can be seen from the accompanying qualitative diagram, that the integrand is piecewise constant for the given frequency responses. |
| − | *Thus, with $f_{\rm G} = 5 \; \rm kHz$ and $f_{\rm N} = f_{\rm G}/2 = 2.5 \; \rm kHz$, we obtain: | + | *Thus, with $f_{\rm G} = 5 \; \rm kHz$ and $f_{\rm N} = f_{\rm G}/2 = 2.5 \; \rm kHz$, we obtain: |
:$$\rho _d = 2 \cdot 2.5\;{\rm{kHz}}\left( { \frac{10^{ - 2}}{\rm{Hz}} + \frac{1}{{{\rm{Hz}}}} } \right) = 5.05 \cdot 10^3 | :$$\rho _d = 2 \cdot 2.5\;{\rm{kHz}}\left( { \frac{10^{ - 2}}{\rm{Hz}} + \frac{1}{{{\rm{Hz}}}} } \right) = 5.05 \cdot 10^3 | ||
\quad \Rightarrow \quad 10\cdot\lg \rho _d \hspace{0.15cm}\underline {= 37.03\;{\rm{dB}}}.$$ | \quad \Rightarrow \quad 10\cdot\lg \rho _d \hspace{0.15cm}\underline {= 37.03\;{\rm{dB}}}.$$ | ||
| − | |||
'''Interpretation''': | '''Interpretation''': | ||
*The matched filter frequency response $H_{\rm MF}(f)$ has exactly the same shape as the integrand sketched above. | *The matched filter frequency response $H_{\rm MF}(f)$ has exactly the same shape as the integrand sketched above. | ||
| − | *If the constant $K_{\rm MF}$ is chosen (arbitrarily) so that in the range $f_{\rm N} \le |f| \le f_{\rm G} | + | *If the constant $K_{\rm MF}$ is chosen (arbitrarily) so that $H_{\rm MF}(f) = 1$ in the range $f_{\rm N} \le |f| \le f_{\rm G}$, then for low frequencies $(|f| < f_{\rm N})$: $H_{\rm MF}(f) = 0.01$. This means: The matched filter favors those frequencies that are only slightly affected by the interference ${\it \Phi}_n(f)$. |
| − | + | *If instead we would use a filter $H(f)$, which gives equal weight to all frequencies up to and including $f_{\rm G}$ (purple curve in the sketch below), <br>the following ratios would result: | |
| − | |||
::$$d_{\rm S}( {T_{\rm D} } ) = G_0 \cdot 2 \cdot f_{\rm G} = 1\;{\rm{V}}, \quad \sigma _d ^2 = 10^{ - 6} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot f_{\rm G} + 10^{ - 8} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot ( {f_{\rm G} - f_{\rm N} } ) = 2.5 \cdot 1.01 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}$$ | ::$$d_{\rm S}( {T_{\rm D} } ) = G_0 \cdot 2 \cdot f_{\rm G} = 1\;{\rm{V}}, \quad \sigma _d ^2 = 10^{ - 6} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot f_{\rm G} + 10^{ - 8} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot ( {f_{\rm G} - f_{\rm N} } ) = 2.5 \cdot 1.01 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}$$ | ||
:$$ \Rightarrow \hspace{0.3cm} \rho _d = \frac {d_{\rm S}( {T_{\rm D} } )^2}{\sigma _d ^2} = \frac{1 \;{\rm{V}}^{\rm{2}}}{2.525 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}} = 396 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \, \rho _d = 25.98 \, {\rm dB}.$$ | :$$ \Rightarrow \hspace{0.3cm} \rho _d = \frac {d_{\rm S}( {T_{\rm D} } )^2}{\sigma _d ^2} = \frac{1 \;{\rm{V}}^{\rm{2}}}{2.525 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}} = 396 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \, \rho _d = 25.98 \, {\rm dB}.$$ | ||
| − | + | *The signal–to–noise ratio is thus about $11\ \rm dB$ worse than when using the matched filter for colored interference. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:19, 23 February 2022
The interference power-spectral density effective on a system can be assumed to be constant in range:
- $$\it{\Phi} _n \left( f \right) = \left\{ \begin{array}{l} N_0 /2 \\ N_1 /2 \\ \end{array} \right.\quad \begin{array}{*{20}c} \rm{for} \\ \rm{for} \\\end{array}\quad \begin{array}{*{20}c} {\left| f \right| \le f_{\rm N} ,} \\ {\left| f \right| > f_{\rm N} .} \\\end{array}$$
- Here, let the power-spectral density $N_1$ in the outer region $|f| > f_{\rm N}$ always be much smaller than $N_0$.
- For example, use the following values:
- $$N_0 = 2 \cdot 10^{ - 6} \;{\rm{V}}^{\rm{2}} /{\rm{Hz}},\quad N_1 = 2 \cdot 10^{ - 8} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$
Such an interference signal $n(t)$ occurs, for example, when the dominant interference source contains only components below the frequency limit $f_{\rm N}$. Due to the unavoidable thermal noise, also for $|f| > f_{\rm N}$ interference power-spectral density is ${\it \Phi}_n(f) \ne 0$.
Further, it holds:
- Let the spectrum $G(f)$ of the useful signal $g(t)$ also be rectangular according to the above diagram.
- Therefore, $g(t)$ has the following curve with $\Delta f = 2 \cdot f_{\rm G}$:
- $$g(t) = G_0 \cdot \Delta f \cdot {\mathop{\rm sinc}\nolimits} \left( { \Delta f \cdot t} \right).$$
- Let the frequency response $H_{\rm E}(f)$ of the receiver filter (German: "Empfangsfilter" ⇒ subscript "E") be optimally matched to the spectrum $G(f)$ and the interference power-spectral density ${\it \Phi}_n(f)$.
- That is, let $H_{\rm E}(f) = H_{\rm MF}(f)$ ⇒ "Matched Filter".
- Let the detection time be simplified $T_{\rm D} = 0$ (acausal system description).
Notes:
- The exercise belongs to the chapter Matched Filter.
- For numerical calculations always use the numerical values
- $$G_0 = 10^{ - 4} \;{\rm{V/Hz}}{\rm{, }}\quad \Delta f = 10\;{\rm{kHz}}.$$
Questions
Solution
(1) Solutions 1 and 3 are correct:
- For all frequencies $|f| > f_{\rm G}$ at which the useful signal $d_{\rm S}(t)$ has spectral components $(G_d(f) \ne 0)$,
the interference power-spectral density is ${\it}\Phi_n(f) = N_0/2$. - Thus, the frequency response of the matched filter is, assuming $T_{\rm D} = 0$:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G(f).$$
- In this case, the optimal frequency response $H_{\rm MF}(f)$, just like $G(f)$, is rectangular with width $\Delta f$.
- Thus, for the useful component of the matched filter output signal $d(t)$ holds:
- $$d_{\rm S}(t)\quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \quad G(f) \cdot H_{\rm MF} (f).$$
- The product of two rectangular functions of equal width again yields a rectangular function.
- It further follows that the output pulse of the matched filter is also $\rm sinc$–shaped.
(2) With white noise one obtains:
- $$\rho _d = \frac{1}{N_0 /2}\int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^2 \, {\rm{d}}f.}$$
- The integral yields the value $G_0^2 \cdot \Delta f$. It follows that:
- $$\rho _d = \frac{G_0 ^2 \cdot \Delta f }{N_0 /2} = \frac{ 10^{ - 8}\,(\rm V/Hz)^2 \;\cdot10^4 \;{\rm{Hz}} }{10^{ - 6}\,\rm V^2/Hz} = 10^2 \quad \Rightarrow \quad 10\lg \rho _d \hspace{0.15cm}\underline { = 20\;{\rm{dB}}}.$$
(3) In general, the SNR for colored interference is:
- $$\rho _d = 2 \cdot \int_0^\infty \frac{\left| {G(f)} \right|^2 }{{\it \Phi}_n (f)} \, {\rm{d}}f.$$
- As can be seen from the accompanying qualitative diagram, that the integrand is piecewise constant for the given frequency responses.
- Thus, with $f_{\rm G} = 5 \; \rm kHz$ and $f_{\rm N} = f_{\rm G}/2 = 2.5 \; \rm kHz$, we obtain:
- $$\rho _d = 2 \cdot 2.5\;{\rm{kHz}}\left( { \frac{10^{ - 2}}{\rm{Hz}} + \frac{1}{{{\rm{Hz}}}} } \right) = 5.05 \cdot 10^3 \quad \Rightarrow \quad 10\cdot\lg \rho _d \hspace{0.15cm}\underline {= 37.03\;{\rm{dB}}}.$$
Interpretation:
- The matched filter frequency response $H_{\rm MF}(f)$ has exactly the same shape as the integrand sketched above.
- If the constant $K_{\rm MF}$ is chosen (arbitrarily) so that $H_{\rm MF}(f) = 1$ in the range $f_{\rm N} \le |f| \le f_{\rm G}$, then for low frequencies $(|f| < f_{\rm N})$: $H_{\rm MF}(f) = 0.01$. This means: The matched filter favors those frequencies that are only slightly affected by the interference ${\it \Phi}_n(f)$.
- If instead we would use a filter $H(f)$, which gives equal weight to all frequencies up to and including $f_{\rm G}$ (purple curve in the sketch below),
the following ratios would result:
- $$d_{\rm S}( {T_{\rm D} } ) = G_0 \cdot 2 \cdot f_{\rm G} = 1\;{\rm{V}}, \quad \sigma _d ^2 = 10^{ - 6} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot f_{\rm G} + 10^{ - 8} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot ( {f_{\rm G} - f_{\rm N} } ) = 2.5 \cdot 1.01 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}$$
- $$ \Rightarrow \hspace{0.3cm} \rho _d = \frac {d_{\rm S}( {T_{\rm D} } )^2}{\sigma _d ^2} = \frac{1 \;{\rm{V}}^{\rm{2}}}{2.525 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}} = 396 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \, \rho _d = 25.98 \, {\rm dB}.$$
- The signal–to–noise ratio is thus about $11\ \rm dB$ worse than when using the matched filter for colored interference.