Difference between revisions of "Channel Coding/Basics of Convolutional Coding"
| Line 55: | Line 55: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Definitions related to convolutional codes:}$ |
| − | * | + | *The <b>code rate</b> results as for the block codes to $R = k/n$.<br> |
| − | * | + | *Perceive $m$ as the <b>memory</b> of the code and the <i>convolutional code</i> itself with ${\rm CC} \ (n, k, m)$.<br> |
| − | * | + | *This gives the <b>constraint length</b> $\nu = m + 1$.<br> |
| − | * | + | *For $k > 1$ one often gives these parameters also in bits: $m_{\rm Bit} = m \cdot k$ resp. $\nu_{\rm Bit} = (m + 1) \cdot k$.<br>}} |
== Gemeinsamkeiten und Unterschiede gegenüber Blockcodes == | == Gemeinsamkeiten und Unterschiede gegenüber Blockcodes == | ||
Revision as of 21:08, 17 September 2022
Contents
# OVERVIEW OF THE THIRD MAIN CHAPTER #
This third main chapter discusses Convolutional codes, first described in 1955 by "Peter Elias" [Eli55][1]. While for linear block codes (see "First Main Chapter") and Reed-Solomon codes (see "Second main chapter") the codeword length is $n$ in each case, the theory of convolutional cdes is based on "semi-infinite" information and code sequences. Similarly, maximum likelihood decoding using the Viterbi algorithm per se yields the entire sequence.
Specifically, this chapter discusses:
- Important definitions for convolutional codes: code rate, memory, influence length, free distance.
- Similarities and differences to linear block codes,
- generator matrix and transfer function matrix of a convolutional code,
- Fractional-rational transfer functions for systematic convolutional codes,
- Description with state transition diagram and trellis diagram,
- termination and puncturing of convolutional codes,
- decoding of convolutional codes ⇒ Viterbi algorithm,
- weight enumerator functions and approximations for the bit error probability.
Requirements and definitions
We consider in this chapter an infinite binary information sequence $\underline{u}$ and divide it into information blocks $\underline{u}_i$ of $k$ bits each. One can formalize this fact as follows:
- \[\underline{\it u} = \left ( \underline{\it u}_1, \underline{\it u}_2, \hspace{0.05cm} \text{...} \hspace{0.05cm}, \underline{\it u}_i , \hspace{0.05cm} \text{...} \hspace{0.05cm}\right ) \hspace{0.3cm}{\rm mit}\hspace{0.3cm} \underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm} \text{...} \hspace{0.05cm}, u_i^{(k)}\right )\hspace{0.05cm},\]
- \[u_i^{(j)}\in {\rm GF(2)}\hspace{0.3cm}{\rm for} \hspace{0.3cm}1 \le j \le k \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \underline{\it u}_i \in {\rm GF}(2^k)\hspace{0.05cm}.\]
In English, such a sequence without negative indices is called semi–infinite .
$\text{Definition:}$ In a Binary Convolutional Code, a codeword $\underline{x}_i$ consisting of $n$ code bit is output at time $i$ :
- \[\underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm} \text{...} \hspace{0.05cm}, x_i^{(n)}\right )\in {\rm GF}(2^n)\hspace{0.05cm}.\]
This results according to
- the $k$ bit of the current information block $\underline{u}_i$, and
- the $m$ previous information blocks $\underline{u}_{i-1}$, ... , $\underline{u}_{i-m}$.
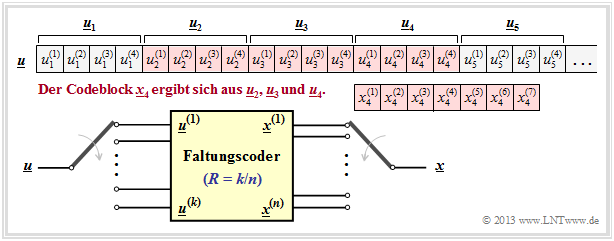
The diagram opposite illustrates this fact for the parameters $k = 4, \ n = 7, \ m = 2$ and $i = 4$.
The $n = 7$ code bits generated at time $i = 4$ $x_4^{(1)}$, ... , $x_4^{(7)}$ may depend (directly) on the $k \cdot (m+1) = 12$ information bits marked in red and are generated by modulo 2 additions.
Also drawn in yellow is a $(n, k)$ convolutional encoder. Note that the vector $\underline{u}_i$ and the sequence $\underline{u}^{(i)}$ are fundamentally different:
- While $\underline{u}_i = (u_i^{(1)}, u_i^{(2)}$, ... , $u_i^{(k)})$ summarizes $k$ at time $i$ parallel information bits,
- denotes $\underline{u}^i = (u_1^{(i)}$, $u_2^{(i)}, \ \text{...})$ the (horizontal) sequence at $i$–th input of the convolutional encoder.
$\text{Definitions related to convolutional codes:}$
- The code rate results as for the block codes to $R = k/n$.
- Perceive $m$ as the memory of the code and the convolutional code itself with ${\rm CC} \ (n, k, m)$.
- This gives the constraint length $\nu = m + 1$.
- For $k > 1$ one often gives these parameters also in bits: $m_{\rm Bit} = m \cdot k$ resp. $\nu_{\rm Bit} = (m + 1) \cdot k$.
Gemeinsamkeiten und Unterschiede gegenüber Blockcodes
Aus der Definition auf der vorherigen Seite ist ersichtlich, dass ein binärer Faltungscode mit $m = 0$ (also ohne Gedächtnis) identisch wäre mit einem binären Blockcode wie in ersten Hauptkapitel beschrieben. Wir schließen diesen Grenzfall aus und setzen deshalb für das Folgende stets voraus:
- Das Gedächtnis $m$ sei größer oder gleich $1$.
- Die Einflusslänge $\nu$ sei größer oder gleich $2$.
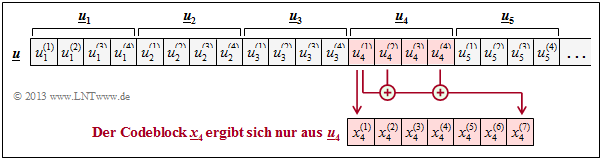
$\text{Beispiel 1:}$ Bei einem $(7, 4)$–Blockcode hängt das Codewort $\underline {x}_4$ nur vom Informationswort $\underline{u}_4$ ab, nicht jedoch von $\underline{u}_2$ und $\underline{u}_3$, wie bei dem beispielhaften Faltungscodes $($mit $m = 2)$ auf der letzten Seite.
Gilt beispielsweise
- $$x_4^{(1)} = u_4^{(1)}, \ x_4^{(2)} = u_4^{(2)},$$
- $$x_4^{(3)} = u_4^{(3)}, \ x_4^{(4)} = u_4^{(4)}$$
sowie
- $$x_4^{(5)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(3)}\hspace{0.05cm},$$
- $$x_4^{(6)} = u_4^{(2)}+ u_4^{(3)}+u_4^{(4)}\hspace{0.05cm},$$
- $$x_4^{(7)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(4)}\hspace{0.05cm},$$
so handelt es sich um einen so genannten systematischen Hamming–Code $\text{HS (7, 4, 3)}$. In der Grafik sind diese speziellen Abhängigkeiten für $x_4^{(1)}$ und $x_4^{(7)}$ rot eingezeichnet.
In gewisser Weise könnte man auch einen $(n, k)$–Faltungscode mit Gedächtnis $m ≥ 1$ als Blockcode interpretieren, dessen Codeparameter $n\hspace{0.05cm}' \gg n$ und $k\hspace{0.05cm}' \gg k$ allerdings sehr viel größere Werte annehmen müssten als die des vorliegenden Faltungscodes. Aufgrund der großen Unterschiede in der Beschreibung, in den Eigenschaften und insbesondere bei der Decodierung betrachten wir aber Faltungscodes in diesem Lerntutorial als etwas völlig Neues. Hierfür sprechen folgende Gründe:
- Ein Blockcodierer setzt Informationsworte der Länge $k$ Bit blockweise in Codeworte mit je $n$ Bit um. Der Blockcode ist dabei um so leistungsfähiger, je größer seine Codewortlänge $n$ ist. Bei gegebener Coderate $R = k/n$ erfordert dies auch eine große Informationswortlänge $k$.
- Dagegen wird die Korrekturfähigkeit eines Faltungscodes im wesentlichen durch sein Gedächtnis $m$ bestimmt. Die Codeparameter $k$ und $n$ werden hier meist sehr klein gewählt $(1, \ 2, \ 3, \ \text{...})$. Von praktischer Bedeutung sind somit nur ganz wenige und zudem sehr einfache Faltungscodes.
- Auch schon bei kleinen Werten für $k$ und $n$ überführt ein Faltungscoder eine ganze Sequenz von Informationsbits $(k\hspace{0.05cm}' → ∞)$ in eine sehr lange Sequenz von Codebits $(n\hspace{0.05cm}' = k\hspace{0.05cm}'/R)$. Ein solcher Code bietet somit oft ebenfalls eine große Korrekturfähigkeit.
- Es gibt effiziente Faltungsdecoder, zum Beispiel den Viterbi–Algorithmus und den BCJR–Algorithmus, die Zuverlässigkeitsinformationen über den Kanal ⇒ Soft–Decision–Input verarbeiten können und Zuverlässigkeitsinformation über das Decodierergebnis ⇒ Soft–Decision–Output liefern.
Rate–1/2–Faltungscodierer
Vorbemerkung: Die beiden Begriffe "Faltungscodierer" und "Faltungscoder" werden in unserem Lerntutorial synonym verwendet und können beliebig ausgetauscht werden.
- Beide Begriffe bezeichnen die konkrete Umsetzung einer Informationssequenz $\underline{u}$ in eine Codesequenz $\underline{x}$.
Die Begriffe "Faltungscodierer" und "Faltungscode" sollte man allerdings nicht verwechseln.
- Unter einem Faltungscode ${\rm CC} \ (n, \ k, \ m)$ ⇒ $R = k/n$ versteht man die Menge aller möglichen Codesequenzen $\underline{x}$, die mit diesem Code unter Berücksichtigung aller möglichen Informationssequenzen $\underline{u}$ (am Eingang) generiert werden kann.
- Es gibt verschiedene Faltungscodierer, die den gleichen Faltungscode realisieren.
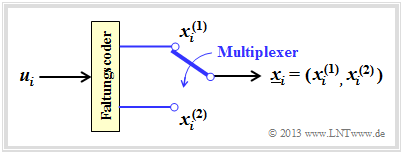
Die obere Grafik zeigt einen $(n = 2, \hspace{0.05cm} k = 1)$–Faltungscodierer.
- Zum Taktzeitpunkt $i$ liegt das Informationsbit $u_i$ am Codereingang an und es wird der 2–Bit–Codeblock $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ ausgegeben.
- Unter Berücksichtigung der (halb–unendlich) langen Informationssequenz $\underline{u}$ ergibt sich das Modell entsprechend der zweiten Grafik.
- Um aus einem einzigen Informationsbit $u_i$ zwei Codebit $x_i^{(1)}$ und $x_i^{(2)}$ generieren zu können, muss der Faltungscodierer mindestens ein Speicherelement beinhalten:
- $$k = 1\hspace{0.05cm}, \ n = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} m \ge 1 \hspace{0.05cm}.$$
$\text{Beispiel 2:}$ Nachfolgend ist ein Faltungscodierer für die Parameter $k = 1, \ n = 2$ und $m = 1$ dargestellt. Das gelb hinterlegte Quadrat kennzeichnet ein Speicherelement. Dessen Beschriftung $D$ ist von Delay abgeleitet.
- Es handelt sich hier um einen systematischen Faltungscodierer, gekennzeichnet durch $x_i^{(1)} = u_i$.
- Der zweite Ausgang liefert $x_i^{(2)} = u_i + u_{i-1}$.
- In der beispielhaften Ausgangssequenz $\underline{x}$ nach Multiplexing sind alle $x_i^{(1)}$ rot und alle $x_i^{(2)}$ blau beschriftet.
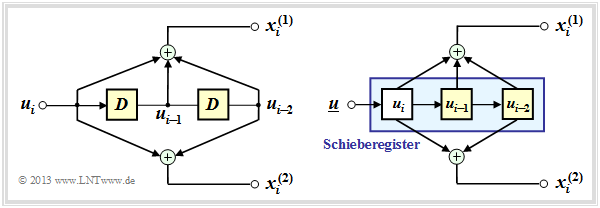
$\text{Beispiel 3:}$ Die Grafik zeigt einen $(n = 2, \ k = 1)$–Faltungscodierers mit $m = 2$ Speicherelementen:
- Links ist das Ersatzschaltbild dargestellt.
- Rechts ist eine Realisierungsform dieses Coders angegeben.
- Die beiden Informationsbits lauten:
- \[x_i^{(1)} = u_{i} + u_{i-1}+ u_{i-2} \hspace{0.05cm},\]
- \[x_i^{(2)} = u_{i} + u_{i-2} \hspace{0.05cm}.\]
- Wegen $x_i^{(1)} ≠ u_i$ handelt es sich hier nicht um einen systematischen Code.
Man erkennt:
- Die Informationssequenz $\underline{u}$ wird in einem Schieberegister der Länge $L = m + 1 = 3$ abgelegt.
- Zum Taktzeitpunkt $i$ beinhaltet das linke Speicherelement das aktuelle Informationsbit $u_i$, das zu den nächsten Taktzeitpunkten jeweils um eine Stelle nach rechts verschoben wird.
- Aus der Anzahl der gelben Quadrate ergibt sich wieder das Gedächtnis $m = 2$ des Coders.
Aus den beiden Darstellungen wird deutlich, dass $x_i^{(1)}$ und $x_i^{(2)}$ jeweils als der Ausgang eines Digitalen Filters über dem Galoisfeld ${\rm GF(2)}$ interpretiert werden kann, wobei beide Filter parallel mit der gleichen Eingangsfolge $\underline{u}$ arbeiten.
Da sich (ganz allgemein) das Ausgangssignal eines Filters aus der Faltung des Eingangssignals mit der Filterimpulsantwort ergibt, spricht man von Faltungscodierung.
Faltungscodierer mit zwei Eingängen
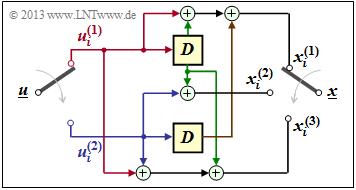
Nun betrachten wir einen Faltungscodierer, der aus $k = 2$ Informationsbits $n = 3$ Codebits generiert.
- Die Informationssequenz $\underline{u}$ wird in Blöcke zu je zwei Bit aufgeteilt.
- Zum Taktzeitpunkt $i$ liegt am oberen Eingang das Bit $u_i^{(1)}$ an und am unteren Eingang $u_i^{(2)}$.
- Für die $n = 3$ Codebits zum Zeitpunkt $i$ gilt dann:
- \[x_i^{(1)} = u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},\]
- \[x_i^{(2)} = u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},\]
- \[x_i^{(3)} = u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.\]
In der Grafik sind die Info–Bits $u_i^{(1)}$ und $u_i^{(2)}$ rot bzw. blau gekennzeichnet, und die vorherigen Info–Bits $u_{i-1}^{(1)}$ und $u_{i-1}^{(2)}$ grün bzw. braun.
Anzumerken ist:
- Das Gedächtnis $m$ ist gleich der maximalen Speicherzellenzahl in einem Zweig ⇒ hier $m = 1$.
- Die Einflusslänge $\nu$ ist gleich der Summe aller Speicherelemente ⇒ hier $\nu = 2$.
- Alle Speicherelemente seien zu Beginn der Codierung (Initialisierung ) auf Null gesetzt.
Der hiermit definierte Code ist die Menge aller möglichen Codesequenzen $\underline{x}$, die sich bei Eingabe aller möglichen Informationssequenzen $\underline{u}$ ergeben. Sowohl $\underline{u}$ als auch $\underline{x}$ seien dabei (zeitlich) unbegrenzt.
$\text{Beispiel 4:}$ Die Informationssequenz sei $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1, \ \text{ ...})$. Daraus ergeben sich die Teilsequenzen $\underline{u}^{(1)} = (0, 1, 0, 1, \ \text{ ...})$ und $\underline{u}^{(2)} = (1, 0, 0, 1, \ \text{ ...})$.
Mit der Festlegung $u_0^{(1)} = u_0^{(2)} = 0$ folgt aus den obigen Gleichungen für die $n = 3$ Codebits
- im ersten Codierschritt $(i = 1)$:
- \[x_1^{(1)} = u_{1}^{(1)} = 0 \hspace{0.05cm},\hspace{0.4cm} x_1^{(2)} = u_{1}^{(2)} = 1 \hspace{0.05cm},\hspace{0.4cm} x_1^{(3)} = u_{1}^{(1)} + u_{1}^{(2)} = 0+1 = 1 \hspace{0.05cm},\]
- im zweiten Codierschritt $(i = 2)$:
- \[x_2^{(1)} =u_{2}^{(1)} + u_{1}^{(1)}+ u_{1}^{(2)} = 1 + 0 + 1 = 0\hspace{0.05cm},\hspace{0.4cm} x_2^{(2)} = u_{2}^{(2)} + u_{1}^{(1)} = 0+0 = 0\hspace{0.05cm},\hspace{0.4cm} x_2^{(3)} = u_{2}^{(1)} + u_{2}^{(2)}+ u_{1}^{(1)} = 1 + 0+0 =1\hspace{0.05cm},\]
- im dritten Codierschritt $(i = 3)$:
- \[x_3^{(1)} =u_{3}^{(1)} + u_{2}^{(1)}+ u_{2}^{(2)} = 0+1+0 = 1\hspace{0.05cm},\hspace{0.4cm} x_3^{(2)} = u_{3}^{(2)} + u_{2}^{(1)} = 0+1=1\hspace{0.05cm},\hspace{0.4cm} x_3^{(3)} =u_{3}^{(1)} + u_{3}^{(2)}+ u_{2}^{(1)} = 0+0+1 =1\hspace{0.05cm},\]
- und schließlich im vierten Codierschritt $(i = 4)$:
- \[x_4^{(1)} = u_{4}^{(1)} + u_{3}^{(1)}+ u_{3}^{(2)} = 1+0+0 = 1\hspace{0.05cm},\hspace{0.4cm} x_4^{(2)} = u_{4}^{(2)} + u_{3}^{(1)} = 1+0=1\hspace{0.05cm},\hspace{0.4cm} x_4^{(3)}= u_{4}^{(1)} + u_{4}^{(2)}+ u_{3}^{(1)} = 1+1+0 =0\hspace{0.05cm}.\]
Damit lautet die Codesequenz nach dem Multiplexer: $\underline{x} = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, \ \text{...})$.
Aufgaben zum Kapitel
Aufgabe 3.1: Analyse eines Faltungscodierers
Aufgabe 3.1Z: Faltungscodes der Rate 1/2
Quellenverzeichnis
- ↑ Elias, P.: Coding for Noisy Channels. In: IRE Conv. Rec. Part 4,pp. 37-47, 1955.