Difference between revisions of "Channel Coding/Error Correction According to Reed-Solomon Coding"
| (63 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü=Reed–Solomon–Codes | + | |Untermenü=Reed–Solomon–Codes and Their Decoding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Reed-Solomon Decoding for the Erasure Channel |
| − | |Nächste Seite= | + | |Nächste Seite=Error Probability and Areas of Application |
}} | }} | ||
| − | == | + | == Block diagram and requirements for RS error correction == |
<br> | <br> | ||
| − | + | As in the chapter [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel#Block_diagram_and_requirements_for_Reed-Solomon_error_detection|"Decoding at the Erasure Channel"]] we consider a transmission system with Reed–Solomon coding characterized by the two code parameters $n=2^m-1$ and $k$. With the generator matrix $\boldsymbol{\rm G}$ the relation between the information word $\underline {u}$ and the code word $\underline {c}$ is: | |
| − | : | + | [[File:EN_KC_T_2_5_S1_neu.png|right|frame|Transmission system with Reed-Solomon coding/decoding and $m$– BSC|class=fit]] |
| − | |||
| − | |||
| − | |||
| − | + | :$$\underline {c} = {\rm enc}(\underline {u}) = \underline {u} \cdot { \boldsymbol{\rm G}} | |
| + | \hspace{0.3cm} {\rm with}$$ | ||
| + | ::$$ \underline {u} = (u_0, u_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_{k-1})\hspace{0.05cm},$$ | ||
| + | ::$$ \underline {c} = (c_0, c_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_{n-1}) | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | The symbols $u_i$ and $c_i$ originate from the field ${\rm GF}(q)$ with | |
| + | :$$q=n+1=2^m.$$ | ||
| + | They are representable by $m$ binary symbols ("bits").<br> | ||
| − | + | A comparison of the upper block diagram with the corresponding [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel#Block_diagram_and_requirements_for_Reed-Solomon_error_detection|$\text{block diagram for Reed-Solomon error detection}$]] shows: | |
| − | + | # The main difference is in the discrete channel model $($highlighted in green$)$. Instead of the erasure channel ("$m$–BEC") now the "$m$–BSC" is considered. For each bit of the code symbol $c_i$ the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{Binary Symmetric Channel}$]] $\rm (BSC)$ is applied. A bit error with respect to the $i$–th bit of the code word results in $y_i \ne c_i$.<br> | |
| + | # In the [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel|"last chapter"]] uncertain bits were already marked by erasures $\rm E$. The task of the "code word finder" $\rm (CWF)$ was to reconstruct the decoding result $\underline {y}$ from the garbled received words $\underline {z}$. | ||
| + | # If the number $e$ of erasures is smaller than the minimum distance $d_{\rm min}$, this succeeds and we get $\underline {z} = \underline {c}$. Otherwise, the code word finder reports that it cannot decode the current received word $\underline {y}$ . A wrong decision $(\underline {z} \ne \underline {c})$ was excluded at the BEC.<br> | ||
| + | # In this chapter, the first decoder block is now referred to as "code word estimator" $\rm (CWS)$. The naming is to make clear that due to the $m$–BSC model, wrong decisions $(\underline {z} \ne \underline {c})$ are inevitable, namely when multiple symbol errors distort the received word $\underline {y}$ to a valid code word.<br><br> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Conclusions:}$ | ||
| + | *The decoder's task is to determine its output vector $\underline {v}$ so that it matches the information word $\underline {u}$ "as well as possible". More precisely formulated: | ||
| − | + | ::<math>{ \rm Pr(block\hspace{0.15cm}error)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.</math> | |
| − | {{ | + | *Because of deterministic mapping $\underline{c} = {\rm enc}(\underline{u})$ and $\underline{v} = {\rm enc}^{-1}(\underline{z})$ holds in the same way: |
| − | |||
| − | ::<math>{ \rm Pr( | + | ::<math>{ \rm Pr(block\hspace{0.15cm}error)} = { \rm Pr}( \underline{z} \ne \underline{c}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.</math>}} |
| − | |||
| − | + | The two blocks highlighted in yellow are not considered further. The focus of the considerations is now the "code word estimator" $\rm (CWS)$ highlighted in red.<br> | |
| + | == Possible code word estimators for Reed-Solomon decoding == | ||
| + | <br> | ||
| + | [[File:EN_KC_T_2_5_S2.png|right|frame|Definition of the error vector $\underline{e}$|class=fit]] | ||
| + | The right sketch of this graphic illustrates the task of the $\rm CWS$ | ||
| + | *where here the channel model "$m$–BSC" is replaced | ||
| − | + | *by the additive »'''error vector'''« | |
| + | :$$\underline{e} = \underline{y} - \underline{c}.$$ | ||
| − | + | The sketch on the left illustrates the relationship between these vectors.<br> | |
| − | |||
| − | |||
| − | |||
| − | + | This task is to be clarified by an example.<br> | |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | Let all symbols be elements of $\rm GF(2^3) \in \{0,\ 1,\ \alpha^1,\ \alpha^2,\ \alpha^3,\ \alpha^4,\ \alpha^5,\ \alpha^6\}$. The adjacent table can be used for conversion | |
| + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representations]] | ||
| + | |||
| + | *between the coefficient representation $($with the order $k_2$, $k_1$, $k_0)$ | ||
| + | |||
| + | *and the exponent representation $($as powers of the primitive element $\alpha).$ | ||
| + | |||
| − | + | In this example, the code word and received word are in coefficient notation: | |
::<math>\underline{c} = \Big ( (010), (001), (100),(010),(100),(111),(111)\Big )\hspace{0.05cm},</math> | ::<math>\underline{c} = \Big ( (010), (001), (100),(010),(100),(111),(111)\Big )\hspace{0.05cm},</math> | ||
::<math>\underline{y} =\Big ( (011), (001), (000),(010),(100),(111),(111)\Big )\hspace{0.05cm}.</math> | ::<math>\underline{y} =\Big ( (011), (001), (000),(010),(100),(111),(111)\Big )\hspace{0.05cm}.</math> | ||
| − | + | ⇒ This results in the following error vector $\underline{e} = \underline{y} - \underline{c}$: | |
::<math>\underline{e} \hspace{0.05cm} = \hspace{0.05cm} \Big ( (001), (000), (100), (000),(000),(000),(000)\Big )\hspace{0.05cm}.</math> | ::<math>\underline{e} \hspace{0.05cm} = \hspace{0.05cm} \Big ( (001), (000), (100), (000),(000),(000),(000)\Big )\hspace{0.05cm}.</math> | ||
| − | + | ⇒ Converted to the exponential representation, we get: | |
::<math>\underline{c} = \Big ( \alpha^1, \hspace{0.09cm}1\hspace{0.09cm}, \alpha^2,\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big )\hspace{0.05cm},</math> | ::<math>\underline{c} = \Big ( \alpha^1, \hspace{0.09cm}1\hspace{0.09cm}, \alpha^2,\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big )\hspace{0.05cm},</math> | ||
| Line 66: | Line 80: | ||
::<math>\underline{e} = \Big ( \hspace{0.09cm}1\hspace{0.09cm}, \hspace{0.09cm}0\hspace{0.09cm}, \hspace{0.05cm}\alpha^2,\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm}\Big )\hspace{0.05cm}.</math>}}<br> | ::<math>\underline{e} = \Big ( \hspace{0.09cm}1\hspace{0.09cm}, \hspace{0.09cm}0\hspace{0.09cm}, \hspace{0.05cm}\alpha^2,\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm}\Big )\hspace{0.05cm}.</math>}}<br> | ||
| + | <u>Note</u> Task of the code word estimator $\rm (CWS)$ is to find the most probable code word to $\underline{y}$ and to pass its result $\underline{z} = \underline{c}_i$ to the following mapping. | ||
| − | + | There are several ways to do this: | |
| − | + | # Hard Decision Maximum Likelihood Decoding $\text{(HD–MLD)}$,<br> | |
| + | # Bounded Distance Decoding $\text{(BDD)}$,<br> | ||
| + | # Decoding "over half the minimum distance".<br><br> | ||
| − | |||
| − | + | <b>Hard Decision Maximum Likelihood Decoding $\text{(HD–MLD)}$:</b><br> | |
| − | + | One chooses from all possible Reed–Solomon code words $\underline{c}_i$ $($hierof there are in total $q^k)$ the one with the least [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|$\text{Hamming distance}$]] to the received word $\underline{y}$. Result: | |
| + | ::<math>\underline{z} = {\rm arg} \min_{\underline{c}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}_{\rm RS}} \hspace{0.1cm} | ||
| + | d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{c}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | ||
| − | + | *The decision here happens on the maximum inference probability ${\rm Pr}(\underline{c}_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y})$ and leads to the best possible result. For more details see [[Channel_Coding/Channel_Models_and_Decision_Structures#Maximum-likelihood_decision_at_the_BSC_channel|"Maximum-likelihood decision Decision at the BSC Channel"]]. | |
| − | + | *A decision is always made even if the number $r$ of symbol errors is larger than the correction capability $t$ of the code. However, in such a case the decoding result is very uncertain.<br> | |
| − | + | *It should be mentioned again that maximum likelihood decoding always decides. Decoding failure is impossible. But of course there are also wrong decisions.<br><br> | |
| − | |||
| − | |||
| − | + | <b>Bounded Distance Decoding $\text{(BDD)}$:</b><br> | |
| − | |||
| − | |||
| − | + | If the number $r$ of symbol errors in the received word $\underline{y}$ is not greater than the correction capability $t = ⌊(d_{\rm min}- 1)/2⌋$ of the code, one can correct the $r$ symbol errors completely. However, it is also true: | |
| + | *The case $r > t$ leads to an abort of the decoding process with no result. In other words: | ||
| + | |||
| + | :*Only those received words towards the center of the sphere are decoded, which lie in a sphere around it with radius $t$. | ||
| + | |||
| + | :*Other received words are marked as undecodable, for example as "erasure".<br><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <b> | + | <b>Decoding over half the minimum distance</b>:<br> |
| − | + | Here also in the case $r > t$ an attempt is made to decode the code word. However, in contrast to $\text{HD–MLD}$, which also decodes beyond half the minimum distance, a decoding failure is not per se excluded here.<br> | |
| − | + | :For the remainder of this chapter, we will deal exclusively with "Bounded Distance Decoding". The reason for this is the enormous complexity of "Maximum Likelihood Decoding" proportional to $q^{n-k}$.<br> | |
| − | == | + | == Bounded Distance Decoding Procedure == |
<br> | <br> | ||
| − | + | In the following, the individual steps of the "bounded distance decoding" $\rm (BDD)$ algorithm are described briefly and in a recipe-like manner. In the next sections, the individual points will be dealt with in more detail and the procedure will be illustrated using typical examples.<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | $\rm (A)$ $\text{Calculation and evaluation of syndrome}$ ⇒ [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD|$\text{Detailed description}$]] | |
| − | + | # Calculate from the received word $\underline{y}$ and the parity-check matrix $\boldsymbol{\rm H }$ of the code the syndrome $\underline {s} = \underline {y} \cdot \boldsymbol{\rm H }^{\rm T}$. | |
| + | # If $\underline {s} =\underline {0}$, set the BDD output $\underline {z} =\underline {y}$ and terminate the decoding process for that received word.<br> | ||
| + | # Otherwise, set the parameter $r = 1$ and continue with step $\rm (B)$ .<br><br> | ||
| − | |||
| − | + | $\rm (B)$ $\text{Determine the actual symbol error count }\ r$ ⇒ [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28B.29:_Set_up.2Fevaluate_the_ELP_coefficient_vector|$\text{Detailed description}$]] | |
| + | # Create and check the equations $\underline {\it \Lambda} _l \cdot\underline {s}^{\rm T} = 0$ for $l = 1,$ ... , $2 \cdot t -r$ assuming that the received word contains exactly $r$ symbol errors.<br> | ||
| + | # $\underline {\it \Lambda} _l $ denotes the generalized [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Error_Locator_Polynomial_-_Definition_and_Properties|$\text{error locator polynomial}$]] $\text{(ELP)}$ coefficient vectors. | ||
| + | # The parameter $t$ denotes the correctability of the code. For the Reed–Solomon codes, uniformly $t = ⌊(n-k)/2 ⌋$.<br> | ||
| + | # If there is a unique solution, then continue with step $\rm (C)$. <br>In the received vector $\underline{y}$ there are then indeed exactly $r$ symbols falsified and in the error vector $\underline{e}$ there are $r$ entries not equal to $0$.<br> | ||
| + | # Otherwise increase $r$ by $1$. If $r ≤ t$ ⇒ repeat step $\rm (B)$ from the beginning: <br>The previously assumed $r$ was obviously too small. Therefore now a new attempt with larger $r$.<br> | ||
| + | # If the new $r$ is greater than the correction capability $t$ of the code, the current word cannot be decoded. End the decoding attempt with an "error message".<br><br> | ||
| − | |||
| − | + | $\rm (C)$ $\text{Localization of the }\ r \text{ error locations}$ ⇒ [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28C.29:_Localization_of_the_error_positions|$\text{Detailed description}$]] | |
| + | # Create the error locator polynomial ${\it \Lambda}(x)$ and find its $r$ zeros in ${\rm GF}(q) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\}$.<br> | ||
| + | # An error at location $i$ is present whenever ${\it \Lambda}(\alpha^{i}) = 0$ .<br><br> | ||
| − | |||
| − | |||
| − | + | $\rm (D)$ $\text{Determination of }\ r \text{ error values and correction}$ ⇒ [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28D.29:_Final_error_correction|$\text{Detailed description}$]] | |
| + | # Now the $r$ error locations are known. Replacing in the received vector $\underline{y}$ the wrong symbols with erasures ⇒ $y_i = \rm E$, if $e_i ≠ 0$, <br>we find the result $\underline{y}$ corresponding to the chapter [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel|"Reed-Solomon Decoding at the Erasure Channel"]].<br> | ||
| + | # '''Or''': From the equation $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$ one arrives at a linear equation system for the faulty symbols $(e_i \ne 0)$ taking advantage of the error-free sites $(e_i = 0)$.<br><br> | ||
| − | + | == Step (A): Evaluation of the syndrome in BDD == | |
| − | + | <br> | |
| − | + | As shown in section [[Channel_Coding/Decoding_of_Linear_Block_Codes#Principle_of_syndrome_decoding|"Principle of Syndrome Decoding"]], the syndrome $\underline{s}$ can be used to decode a linear code. | |
| − | |||
| − | + | *With the received word $\underline{y}$ equal to code word $\underline{c}$ plus error vector $\underline{e}$ applies: | |
| − | |||
| − | |||
::<math>\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}= | ::<math>\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}= | ||
| Line 142: | Line 158: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *Since always $\underline {c} \cdot { \boldsymbol{\rm H }}^{\rm T} =\underline {0}$ holds, it follows from $\underline{s}= \underline{0}$ also $\underline {e} \cdot { \boldsymbol{\rm H }}^{\rm T} =\underline{0}$. That is: | |
| − | |||
| − | * | + | *With very high probability, from $\underline{s}= \underline{0}$ it is also possible to infer $\underline{e}= \underline{0}$ and thus also the correct decoding result $\underline{z}= \underline{y}$. The decoding process would be finished.<br> |
| + | |||
| + | *But there are also error patterns $\underline{e} \ne \underline{0}$ that lead to the syndrome $\underline{s}= \underline{0}$. Such patterns certainly contain more than $t$ symbol errors. | ||
| + | |||
| + | *So here it makes also sense to abort the decoding process. All subsequent calculations would also not lead to success.<br><br> | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | This and the following examples in the next sections are always based on the Reed–Solomon code $\text{RSC (7, 3, 5)}_8$ so that the conversions given in the graph in $\rm GF(2^3)$ can be used. The received words are: | |
| + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representations]] | ||
| − | ::<math>\underline{y}=\big (\alpha^3,\hspace{0. | + | ::<math>\underline{y}=\big (\alpha^3,\hspace{0.08cm} 1,\hspace{0.08cm} 0, \hspace{0.08cm}\alpha^1, \hspace{0.08cm} \alpha^2, \hspace{0.08cm} \alpha^5, \hspace{0.08cm} \alpha^5 \big).</math> |
| − | + | *With the [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes#Generator_matrix_and_parity-check_matrix|$\text{parity-check matrix}$]] $\boldsymbol{\rm H }$ results for the syndrome: | |
::<math>\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H } }^{\rm T}= | ::<math>\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H } }^{\rm T}= | ||
| Line 168: | Line 187: | ||
\alpha^5 & \alpha^3 & \alpha^1 & \alpha^6 \\ | \alpha^5 & \alpha^3 & \alpha^1 & \alpha^6 \\ | ||
\alpha^6 & \alpha^5 & \alpha^4 & \alpha^3 | \alpha^6 & \alpha^5 & \alpha^4 & \alpha^3 | ||
| − | \end{pmatrix} </math> | + | \end{pmatrix}. </math> |
| − | ::<math>\ | + | *These vector–matrix multiplications gives the result: |
| + | ::<math>\underline {s} \hspace{-0.05cm} = \hspace{-0.05cm} (\alpha^3 , \alpha^3 , \alpha^3 , \alpha^3) + (\alpha^1 , \alpha^2 , \alpha^3 , \alpha^4) + (0,0,0,0) \hspace{-0.05cm}+\hspace{-0.05cm} (\alpha^4,1,\alpha^3,\alpha^6)+(\alpha^6,\alpha^3,1,\alpha^4)\hspace{-0.05cm}+\hspace{-0.05cm}(\alpha^3,\alpha^1,\alpha^6,\alpha^4) \hspace{-0.05cm}+\hspace{-0.05cm} (\alpha^4,\alpha^3,\alpha^2,\alpha^1)</math> | ||
::<math>\Rightarrow \hspace{0.3cm} \underline {s} = \text{...} \hspace{0.05cm}= | ::<math>\Rightarrow \hspace{0.3cm} \underline {s} = \text{...} \hspace{0.05cm}= | ||
(\alpha^5,\alpha^2,\alpha^3,\alpha^1) \hspace{0.05cm}.</math> | (\alpha^5,\alpha^2,\alpha^3,\alpha^1) \hspace{0.05cm}.</math> | ||
| − | + | *So the received word was falsified. Otherwise it should have resulted in $\underline{e}= \underline{0} = (0, 0, 0, 0)$ .<br> | |
| − | |||
| − | == Error Locator | + | The description of the decoding process at $\text{RSC (7, 3, 5)}_8$ is continued in [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28B.29:_Set_up.2Fevaluate_the_ELP_coefficient_vector|$\text{Example 4}$]] }}<br> |
| + | |||
| + | == Error Locator Polynomial - Definition and Properties == | ||
<br> | <br> | ||
| − | + | After the syndrome calculation in step $\rm (A)$ with the result $\underline{s} \ne \underline{0}$ we know, | |
| − | * | + | *that the received word $\underline{y}$ does not match the code word $\underline{c}$, respectively<br> |
| − | * | + | *that the error vector $\underline{e} = (e_0, \hspace{0.05cm}e_1, \hspace{0.05cm}\text{ ...}\hspace{0.05cm} , e_{n-1})$ certainly includes elements not equal to "$0$". <br><br> |
| − | + | However, we do not know how many symbols were falsified $(0 < r ≤ n)$ nor we can name the positions of the error locations $(e_i ≠ 0)$ in the error vector $\underline{c}$. An approach to this task is provided by the so-called "error locator polynomial" introduced by [https://en.wikipedia.org/wiki/W._Wesley_Peterson $\text{William Wesley Peterson}$] ⇒ see [Pet60]<ref name ='Pet60'>Peterson, W.W: Encoding and Error-correction Procedures for the Bose-Chaudhuri codes. IRE Transactions on Information Theory, IT-6:459{470), 1960.</ref>. It is also known as "key equation".<br> | |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Let it be known that exactly $r$ elements of the error vector $\underline{e}$ are non-zero, recognizable by [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|$\text{Hamming weight}$]] $w_{\rm H}(\underline{e}) = r$. | ||
| + | *Also let the quantity ${I}_{\rm EP}$ of error positions be known: | ||
| − | {{ | + | ::<math>I_{\rm EP} = \{ i \hspace{0.1cm}\vert \hspace{0.1cm} e_i \ne 0,\hspace{0.1cm} 0 \le i < n \}\hspace{0.05cm}.</math> |
| − | |||
| − | + | *Then for the »'''Error Locator Polynomial'''« $\rm (ELP)$: | |
| − | + | ::<math>{\it \Lambda}(x)=x \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm FP} }(x-\alpha^i) =x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ].</math>}} | |
| − | |||
| − | + | ⇒ From the error locator polynomial we know: | |
| − | * | + | *Because of the factor $x$ in front of the product sign: ${\it \Lambda}(x= 0) = 0$.<br> |
| − | * | + | *Other $r$ zeros result for $x = \alpha^{i}$ with $i \in I_{\rm EP}$, that is, for all error positions.<br> |
| − | * | + | *In contrast, the error locator polynomial for $i ∉ I_{\rm EP}$ ⇒ $e_i = 0$ has no zero: ${\it \Lambda}(x= \alpha^{i}) \ne0$.<br><br> |
| − | + | ⇒ So we search for the $r$ non–trivial zeros of ${\it \Lambda}(x)$ with argument $x ∈ {\rm GF}(q) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\}$. If we succeed, | |
| + | :*we know the $r$ error positions, | ||
| + | :*but not yet the actual error values $e_i ∈ {\rm GF}(q)$.<br> | ||
| − | [[File: | + | {{GraueBox|TEXT= |
| − | + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representations]] | |
| − | $\text{ | + | $\text{Example 3:}$ |
| − | + | Let $n=7$ ⇒ $q=8$, $r=2$ and $I_{\rm FP} = \{2, \hspace{0.05cm}4\}$: [[File:P ID2551 KC T 2 5 S5a.png]]<br> | |
| − | + | *Thus for the "error locator poynomial" from ${\rm GF}(2^3)$ is obtained: | |
::<math>{\it \Lambda}(x)=x \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^4)= x \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^4) =x \cdot \big [x^2 \hspace{-0.05cm}+ \hspace{-0.05cm}(\alpha^2 + \alpha^4) \cdot x + \alpha^6\big ] </math> | ::<math>{\it \Lambda}(x)=x \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^4)= x \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^4) =x \cdot \big [x^2 \hspace{-0.05cm}+ \hspace{-0.05cm}(\alpha^2 + \alpha^4) \cdot x + \alpha^6\big ] </math> | ||
::<math>\Rightarrow \hspace{0.3cm} {\it \Lambda}(x)= x \cdot \big [\alpha^6 + \alpha \cdot x + x^2\big ]\hspace{0.05cm}.</math> | ::<math>\Rightarrow \hspace{0.3cm} {\it \Lambda}(x)= x \cdot \big [\alpha^6 + \alpha \cdot x + x^2\big ]\hspace{0.05cm}.</math> | ||
| − | + | *The other zeros $($except for $x = 0)$ arise naturally here for $x = \alpha^2$ and $x = \alpha^4$, as a calculation shows: | |
::<math>{\it \Lambda}(x = \alpha^2)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^2 + (\alpha^2)^2\big ] = x \cdot \big [\alpha^6 + \alpha^3 + \alpha^4 \big ]= 0\hspace{0.05cm},</math> | ::<math>{\it \Lambda}(x = \alpha^2)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^2 + (\alpha^2)^2\big ] = x \cdot \big [\alpha^6 + \alpha^3 + \alpha^4 \big ]= 0\hspace{0.05cm},</math> | ||
::<math> {\it \Lambda}(x = \alpha^4)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^4 + (\alpha^4)^2\big ] =x \cdot \big [\alpha^6 + \alpha^5 + \alpha \big ]= 0\hspace{0.05cm}.</math>}}<br> | ::<math> {\it \Lambda}(x = \alpha^4)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^4 + (\alpha^4)^2\big ] =x \cdot \big [\alpha^6 + \alpha^5 + \alpha \big ]= 0\hspace{0.05cm}.</math>}}<br> | ||
| − | + | For further derivation, we always assume the $\text{RSC (7, 3, 5)}_8$ with the following parameter values: | |
| − | |||
| − | :$$n=7, \hspace{0.3cm}k = 3, \hspace{0.3cm}d_{\rm min} = 5 \ \Rightarrow | + | :$$n=7, \hspace{0.3cm}k = 3, \hspace{0.3cm}d_{\rm min} = 5 \ \Rightarrow \ t = (d_{\rm min} -1/2) = 2.$$ |
| − | + | *Let the number of symbol errors be $r = t = 2$. Thus the system of equations to be solved with the auxiliary variables $L_i = {\it \Lambda}(\alpha^{i})$: | |
::<math>L_0 = {\it \Lambda }(\alpha^0) = \alpha^0 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^0)^1 + (\alpha^0)^2 \right ] = {\it \lambda}_0 \cdot 1 + {\it \lambda}_1 \cdot 1 + 1 \hspace{0.05cm},</math> | ::<math>L_0 = {\it \Lambda }(\alpha^0) = \alpha^0 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^0)^1 + (\alpha^0)^2 \right ] = {\it \lambda}_0 \cdot 1 + {\it \lambda}_1 \cdot 1 + 1 \hspace{0.05cm},</math> | ||
| Line 233: | Line 255: | ||
::<math> L_6 = {\it \Lambda }(\alpha^6) = \alpha^6 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^6)^1 + (\alpha^6)^2 \right ] = {\it \lambda}_0 \cdot \alpha^6 + {\it \lambda}_1 \cdot \alpha^{12} + \alpha^{18} \hspace{0.05cm}.</math> | ::<math> L_6 = {\it \Lambda }(\alpha^6) = \alpha^6 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^6)^1 + (\alpha^6)^2 \right ] = {\it \lambda}_0 \cdot \alpha^6 + {\it \lambda}_1 \cdot \alpha^{12} + \alpha^{18} \hspace{0.05cm}.</math> | ||
| − | In | + | *In vector form, this system of equations with the auxiliary vector is $\underline{L} = (L_0, \hspace{0.05cm}L_1, \hspace{0.05cm}L_2,\hspace{0.05cm}L_3,\hspace{0.05cm}L_4,\hspace{0.05cm}L_5,\hspace{0.05cm}L_6)$: |
::<math>\underline {L}^{\rm T}=\begin{pmatrix} | ::<math>\underline {L}^{\rm T}=\begin{pmatrix} | ||
| Line 261: | Line 283: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *We now expand the ELP coefficient vector $\underline {\it \Lambda }$ by appending zeros to the length $n-k$. Thus, in the considered example, we obtain ${\it \Lambda } = ( \lambda_0,\hspace{0.05cm}\lambda_1,\hspace{0.05cm}1, \hspace{0.05cm}0)$ and the following vector equation: | |
::<math>\underline {L}^{\rm T} | ::<math>\underline {L}^{\rm T} | ||
| Line 282: | Line 304: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *With this we have achieved: | |
| − | + | # The $7× 3$ matrix has now become a $7× 4$ matrix. | |
| − | + | # The fourth column can actually be filled arbitrarily, since all elements are multiplied by zeros. | |
| − | + | # The addition chosen here gives the transposed [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes#Generator_matrix_and_parity-check_matrix| $\text{parity-check matrix}$]] of $\text{RSC (7, 3, 5)}_8$. | |
| − | + | # Thus, one can write for the last vector equation: | |
| − | ::<math>\underline {L}^{\rm T} = { \boldsymbol{\rm H }}^{\rm T} \cdot \underline {\it \Lambda }^{\rm T} | + | :::<math>\underline {L}^{\rm T} = { \boldsymbol{\rm H }}^{\rm T} \cdot \underline {\it \Lambda }^{\rm T} |
\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline {L} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline {L} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *But since for the error locations $(e_i ≠ 0)$ always $L_i = {\it \Lambda}(\alpha^{i}) = 0$ holds, the product $L_i \cdot e_i \equiv 0$ and one obtains as determining equation for the zeros of the error locator polynomial: | |
| − | ::<math>\underline {L}^{\rm T} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | + | :::<math>\underline {L}^{\rm T} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |
\underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
\underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 | \underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 | ||
| Line 300: | Line 322: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Important intermediate result:}$ The non-trivial zeros $\lambda_0$, $\lambda_1$, ... $(=0)$ of the error locator polynomial ${\it \Lambda}(x)$ must always satisfy the vector equation $\underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 $ . |
| + | *Hereby denotes $\underline {\it \Lambda }$ the $\rm ELP$ coefficient vector. | ||
| − | + | * $\underline {s } = \underline {y }\cdot \boldsymbol{\rm H }^{\rm T} $ gives the [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD|$\text{syndrome}$]].}}<br> | |
| − | |||
| − | * $\underline {s } = \underline {y }\cdot \boldsymbol{\rm H }^{\rm T} $ | ||
| − | == | + | == Step (B): Set up/evaluate the ELP coefficient vector == |
<br> | <br> | ||
| − | + | Before we can consider this intermediate result for step $\rm (B)$ some generalizations need to be made. | |
| − | * | + | [[File:P ID2550 KC T 2 5 S3 v1.png|right|frame|Shifted ELP coefficient vectors|class=fit]] |
| + | The reason for this is: | ||
| + | *The relationship $\underline {\it \lambda } \cdot \underline {s}^{\rm T} = 0 $ yields only a single equation of determination. | ||
| + | |||
| + | *Thus the problem can be solved for $r = 1$ if one is sure that indeed only one symbol has been falsified.<br> | ||
| − | * | + | *If one is not sure of this, but nevertheless performs the calculation for $r = 1$, one still needs a second equation (or even several) to verify the assumption.<br><br> |
| − | + | The property of the [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Error_Locator_Polynomial_-_Definition_and_Properties|$\text{error locator polynomial}$]] that ${\it \Lambda}(\alpha^{i}) = 0$ only for $e_i ≠ 0$ $($that means: the $i$–th symbol is falsified$)$ is preserved when multiplying ${\it \Lambda}(x)$ by arbitrary powers of $x$. | |
| − | + | Each multiplication by $x$ implies a shift of one place to the right for the ELP coefficient vector.<br> | |
| + | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The $\text{generalized ELP coefficient vectors}$ $\underline {\it \Lambda }_l$ result from successive shifts with respect to $\underline {\it \Lambda }_l$: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ::<math>{\it \Lambda}_l(x)=x^l \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm EP} }(x-\alpha^i) =x^l \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ]\hspace{0.05cm}.</math> | |
| − | |||
| − | |||
| − | |||
| + | In this defining equation, $\underline {\it \Lambda }_1$ corresponds to the previous $\underline {\it \Lambda }$.}} | ||
| − | |||
| − | |||
| − | + | The upper graph shows the occupancy under the assumption of $r$ error locations in the error vector $\underline {e}$ for | |
| + | *$r=1$ in the left panel (with blue background), | ||
| + | *$r=2$ in the middle area (with red background), | ||
| + | *$r=3$ in the right area (with green background). | ||
| − | |||
| − | + | One recognizes: | |
| + | # The length of all $\underline {\it \lambda }_l$ is always $n-k$. Each vector contains respectively $r$ coefficients $\lambda_0$, $\lambda_1$, ... , $\lambda_{r-1}$ ⇒ $0 ≤ i < r$ and one "1". <br>The remainder of each vector is padded with zeros.<br> | ||
| + | # For each $r$ there are exactly $n-k-r$ coefficient vectors $\underline {\it \Lambda }_l$, where $\underline {\it \Lambda }_l$ results from $\underline {\it \Lambda }_{l-1} $ always by right shifting by one position. <br>The vector $\underline {\it \Lambda }_{n-k-r}$ always ends with a $1$.<br> | ||
| + | # The equation system $\underline {\it \Lambda }_l \cdot \underline {s}^{\rm T} = 0 $ therefore leads to $n-k-r$ equations. <br>The chosen approach for $r$ is only correct if all equations lead to the same results for $\lambda_0$, ... , $\lambda_{r-1}$ .<br> | ||
| + | # If this is not the case, one has to increase $r$ and thus work on a new equation system, and this until a unique solution results from all equations for the current $r$. If the finally $r$ is greater than the correctability $t$ of the code, the calculation can be terminated. The pending received word $\underline {y}$ is then not decodable.<br> | ||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representation]] | ||
| + | $\text{Example 4:}$ The conditions stated in the [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD| $\text{Example 2}$]] still apply: | ||
| + | # There, due to the syndrome $\underline {s} = (\alpha^5,\ \alpha^2,\ \alpha^3,\ \alpha^1) ≠ \underline {0}$ it was also demonstrated that the received vector $\underline {y}$ was falsified ⇒ error vector $\underline {e} \ne {0}$. | ||
| + | # Not known, however, is the actual symbol error count $r$.<br> | ||
| − | + | *Assuming a single falsified symbol $(r= 1)$ we obtain the following system of equations $($written here in matrix form$)$: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
::<math>\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= | ::<math>\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= | ||
| Line 372: | Line 392: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *This equation system gives three different solutions for $\lambda_0$, which is not purposeful:<br> | |
| − | ::<math>\text{ | + | ::<math>\text{line 1:}\hspace{0.5cm}\alpha^5 \cdot \lambda_0 + \alpha^2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |
\lambda_0 = \alpha^{2-5}= \alpha^{-3}= \alpha^{4}\hspace{0.05cm},</math> | \lambda_0 = \alpha^{2-5}= \alpha^{-3}= \alpha^{4}\hspace{0.05cm},</math> | ||
| − | ::<math>\text{ | + | ::<math>\text{line 2:}\hspace{0.5cm}\alpha^2 \cdot \lambda_0 + \alpha^3 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |
\lambda_0 = \alpha^{3-2}= \alpha\hspace{0.05cm},</math> | \lambda_0 = \alpha^{3-2}= \alpha\hspace{0.05cm},</math> | ||
| − | ::<math>\text{ | + | ::<math>\text{line 3:}\hspace{0.5cm}\alpha^3 \cdot \lambda_0 + \alpha^1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |
\lambda_0 = \alpha^{1-3}= \alpha^{-2} = \alpha^{5} \hspace{0.05cm}.</math> | \lambda_0 = \alpha^{1-3}= \alpha^{-2} = \alpha^{5} \hspace{0.05cm}.</math> | ||
| − | + | *Therefore, we now set up another equation system, assuming $r = 2$: | |
::<math>\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= | ::<math>\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= | ||
| Line 397: | Line 417: | ||
0\\ | 0\\ | ||
0 | 0 | ||
| − | \end{pmatrix} </math> | + | \end{pmatrix}\hspace{0.05cm}. </math> |
| − | + | *This leads to two equations for $\lambda_0$ and $\lambda_1$: | |
| − | ::<math>\alpha^5 \cdot \lambda_0 + \alpha^2 \cdot \lambda_1 + \alpha^3 = 0 \hspace{0.05cm},\hspace{0.5cm}\alpha^2 \cdot \lambda_0 + \alpha^3 \cdot \lambda_1 + \alpha^1 | + | ::<math>\alpha^5 \cdot \lambda_0 + \alpha^2 \cdot \lambda_1 + \alpha^3 = 0 \hspace{0.05cm},\hspace{0.5cm}\alpha^2 \cdot \lambda_0 + \alpha^3 \cdot \lambda_1 + \alpha^1 = 0 \hspace{0.05cm}.</math> |
| − | + | *This equation system is now clearly solvable. One gets $\lambda_0 = \alpha^2$ and $\lambda_1 = \alpha^6$. This means: | |
| − | + | # The assumption that indeed $r = 2$ positions of the received vector $\underline {y}$ have been distorted is correct.<br> | |
| − | + | # But it is not yet known which positions have been falsified. So much for now: | |
| − | + | # It is not symbol positions '''2''' and '''6''', but the positions '''0''' and '''2''', as shown in the following $\text{Example 5}$ (next section).}}<br> | |
| − | == | + | == Step (C): Localization of the error positions == |
<br> | <br> | ||
| − | + | After processing step $\rm(B)$ are known: | |
| − | + | # the number $r$ of error locations $e_i ≠ 0$ in the vector $\underline {e} = (e_0, \hspace{0.05cm}\text{... }\hspace{0.05cm}, e_i, \hspace{0.05cm}\text{... }\hspace{0.05cm}, e_{n-1})$,<br> | |
| + | # the coefficients $\lambda_0, \hspace{0.05cm}\text{... }\hspace{0.05cm} , \lambda_{r-1}$ of the error locator polynomial..<br><br> | ||
| + | |||
| + | Now the set of error positions has to be determined: $I_{\rm EP} = \{ i \hspace{0.1cm}| \hspace{0.1cm} e_i \ne 0,\hspace{0.3cm} 0 \le i < n \}\hspace{0.05cm}.$ | ||
| − | * | + | There are two ways to do this $($both methods are used in the following example$)$: |
| + | *the so-called "Chien search", in which one determines the searched zeros by inserting the possible code symbols except the zero symbol ⇒ $(\alpha^0, \text{... }, \alpha^i, \text{... },\alpha^{n-1})$ into the the error locator polynomial,<br> | ||
| − | + | *the evaluation of the equation $\underline {L} = (L_0, \text{... }, L_i, \text{... },L_{n-1} ) = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }}$ with the abbreviation $L_i = {\it \Lambda}(\alpha^i)$.<br> | |
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 5:}$ | ||
| + | In [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28B.29:_Set_up.2Fevaluate_the_ELP_coefficient_vector| $\text{Example 4}$]] it was determined according to the constraints specified in [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD| $\text{Example 2}$]] stated boundary conditions determined that | ||
| + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representations]] | ||
| − | + | # $r= 2$ symbol errors are present, and | |
| − | + | # the ELP coefficients are $\lambda_0 = \alpha^2$ and $\lambda_1 = \alpha^6$. | |
| − | + | ||
| − | + | ||
| − | + | This results in the following error locator polynomial: | |
::<math>{\it \Lambda}(x)=x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+x^2 \big ] | ::<math>{\it \Lambda}(x)=x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+x^2 \big ] | ||
=x \cdot \big [\alpha^2 + \alpha^6 \cdot x+x^2 \big ]\hspace{0.05cm}.</math> | =x \cdot \big [\alpha^2 + \alpha^6 \cdot x+x^2 \big ]\hspace{0.05cm}.</math> | ||
| − | + | ⇒ According to the Chien search one gets | |
| − | |||
| − | ::<math>{\it \Lambda}(\alpha^0)\hspace{0.15cm} = \hspace{0.15cm}\alpha^0 \cdot \big [ \alpha^2 + \alpha^6 \cdot 1 + 1 \big ] = \alpha^2 + (\alpha^2 + 1) + 1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm | + | ::<math>{\it \Lambda}(\alpha^0)\hspace{0.15cm} = \hspace{0.15cm}\alpha^0 \cdot \big [ \alpha^2 + \alpha^6 \cdot 1 + 1 \big ] = \alpha^2 + (\alpha^2 + 1) + 1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zero} }\hspace{0.05cm},</math> |
| − | ::<math>{\it \Lambda}(\alpha^1)\hspace{0.15cm} = \hspace{0.15cm}\alpha^1 \cdot \big [\alpha^2 + \alpha^6 \cdot \alpha^1 + \alpha^2\big ]= \alpha^1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm | + | ::<math>{\it \Lambda}(\alpha^1)\hspace{0.15cm} = \hspace{0.15cm}\alpha^1 \cdot \big [\alpha^2 + \alpha^6 \cdot \alpha^1 + \alpha^2\big ]= \alpha^1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm No\hspace{0.15cm} zero}\hspace{0.05cm},</math> |
::<math>{\it \Lambda}(\alpha^2)\hspace{0.15cm} = \hspace{0.15cm}\alpha^2 \cdot \big [ \alpha^2 + \alpha^6 \cdot \alpha^2 + \alpha^4 \big ] =\alpha^4 + \alpha^{10} + \alpha^6 = \text{...} | ::<math>{\it \Lambda}(\alpha^2)\hspace{0.15cm} = \hspace{0.15cm}\alpha^2 \cdot \big [ \alpha^2 + \alpha^6 \cdot \alpha^2 + \alpha^4 \big ] =\alpha^4 + \alpha^{10} + \alpha^6 = \text{...} | ||
= \hspace{0.15cm}0 | = \hspace{0.15cm}0 | ||
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm | + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zero} }\hspace{0.05cm}.</math> |
| − | + | Thus the two error positions with $i = 0$ and $i = 2$ are found ⇒ the error vector is: $\underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)$ .<br> | |
| − | + | ⇒ The vector equation $\underline {L} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H } }$ gives the same result in a more compact form: | |
::<math>\underline {L} = \underline{\it \Lambda} \cdot { \boldsymbol{\rm H } } = (\alpha^2, \alpha^6, 1, 0) \cdot | ::<math>\underline {L} = \underline{\it \Lambda} \cdot { \boldsymbol{\rm H } } = (\alpha^2, \alpha^6, 1, 0) \cdot | ||
| Line 458: | Line 482: | ||
\underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)\hspace{0.05cm}.</math> | \underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)\hspace{0.05cm}.</math> | ||
| − | + | The example continues with the $\text{Example 6}$ in the next section}}.<br> | |
| − | == | + | == Step (D): Final error correction == |
<br> | <br> | ||
| − | + | In the last step the $r$ symbol errors have to be corrected, whose positions are known after completion of step $\rm (C)$ : | |
| − | * | + | *Marking the error positions in the received word $\underline {y}$ as erasures $\rm E$, the corresponding code word $\underline {z}$ can be found according to the description in chapter [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel|"Reed-Solomon decoding at the erasure channel"]].<br> |
| − | * | + | *A second possibility offers the determination of the error vector $\underline {e}$ from the equation $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$ and correcting accordingly $\underline {z} = \underline {y} - \underline {e} $. This procedure is the basis of the following example.<br><br> |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6:}$ We consider again the $\text{RSC (7, 3, 5)}_8$. In [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD| $\text{Example 2}$]] was |
| − | * | + | *the received word given with $\underline{y}=\big (\alpha^3,\hspace{0.09cm} 1,\hspace{0.09cm} 0, \hspace{0.09cm}\alpha^1, \hspace{0.09cm} \alpha^2, \hspace{0.09cm} \alpha^5, \hspace{0.09cm} \alpha^5 \big),$ and |
| − | * | + | |
| + | *from this determined the syndrome $\underline{s}=\big (\alpha^5,\hspace{0.09cm}\alpha^2, \hspace{0.09cm} \alpha^3, \hspace{0.09cm} \alpha^1\big)$. | ||
| − | + | According to the calculations in [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28C.29:_Localization_of_the_error_positions| $\text{Example 5}$]] the error vector is $\underline {e} = (e_0,\ 0,\ e_2,\ 0,\ 0,\ 0,\ 0)$. <br> | |
| − | + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representations]] | |
| + | From $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$ we now obtain the following governing equations for the error values $e_0$ and $e_2$: | ||
::<math>\underline {e} \cdot \boldsymbol{\rm H }^{\rm T}= \begin{pmatrix} | ::<math>\underline {e} \cdot \boldsymbol{\rm H }^{\rm T}= \begin{pmatrix} | ||
| Line 493: | Line 518: | ||
\alpha^5 & \alpha^2 & \alpha^3 & \alpha^1 | \alpha^5 & \alpha^2 & \alpha^3 & \alpha^1 | ||
\end{pmatrix} </math> | \end{pmatrix} </math> | ||
| − | ::<math>\Rightarrow \hspace{0.3cm}e_0 \cdot (1, 1, 1, 1) + e_2 \cdot ( | + | ::<math>\Rightarrow \hspace{0.3cm}e_0 \cdot (1,\ 1,\ 1,\ 1) + e_2 \cdot (\alpha^2,\ \alpha^4,\ \alpha^6,\ \alpha^1)\stackrel{!}{=} |
| − | ( \alpha^5, \alpha^2, \alpha^3, \alpha^1)</math> | + | ( \alpha^5,\ \alpha^2,\ \alpha^3,\ \alpha^1)</math> |
::<math>\Rightarrow \hspace{0.3cm} | ::<math>\Rightarrow \hspace{0.3cm} | ||
e_0 + e_2 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.2cm} | e_0 + e_2 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.2cm} | ||
| Line 501: | Line 526: | ||
e_0 + e_2 \cdot \alpha^1 = \alpha^1\hspace{0.05cm}.</math> | e_0 + e_2 \cdot \alpha^1 = \alpha^1\hspace{0.05cm}.</math> | ||
| + | *All equations lead to the result $e_0 = 1$ and $e_2 =\alpha^2$. | ||
| − | + | *Thus the corrected code word with $\underline {y} = (\alpha^3,\hspace{0.09cm} 1,\hspace{0.09cm} 0,\hspace{0.09cm} \alpha^1,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} \alpha^5,\hspace{0.09cm} \alpha^5)$ and $\underline {e}= (1,\hspace{0.09cm} 0,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} 0,\hspace{0.09cm} 0,\hspace{0.09cm} 0,\hspace{0.09cm} 0)$: | |
::<math>\underline {z} = \underline {y} - \underline {e} = \underline {y} + \underline {e}= | ::<math>\underline {z} = \underline {y} - \underline {e} = \underline {y} + \underline {e}= | ||
| − | (\alpha^1,\hspace{0. | + | (\alpha^1,\hspace{0.09cm} 1,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} \alpha^1,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} \alpha^5,\hspace{0.09cm} \alpha^5)\hspace{0.05cm}. </math> |
| − | + | *This is a valid code word of the $\text{RSC (7, 3, 5)}_8$.}}<br> | |
| − | == | + | == Fast Reed-Solomon decoding == |
<br> | <br> | ||
| − | + | The class of Reed–Solomon codes was already introduced in 1960 by the publication [RS60]<ref name='RS60'>Reed, I.S.; Solomon, G.: Polynomial Codes over Certain Finite Fields. J. Siam, Vol. 8, pp. 300-304, 1960.</ref>. However, their efficient decoding was not possible until a decade or two later.<br> | |
| + | |||
| + | In the last sections we have demonstrated the so-called "Petersen algorithm" including the "Chien search" on the example of $\text{RSC (7, 3, 5)}_8$ which can correct up to $t = 2$ errors. | ||
| + | *The decoding process focused on setting up and solving the key equation where the zeros of a degree-2 polynomial in the field $\rm GF(7)$ had to be found. | ||
| − | + | *It was to be recognized that already this algebraic decoding is connected with large expenditure.<br> | |
| − | |||
| − | + | For codes used in practice with large code word length $n$ and high correctability $t$ the decoding effort would explode if faster decoding algorithms had not been found. | |
| − | + | :For example, in the Reed–Solomon code $\text{RSC (255, 223, 33)}_{256}$, mentioned early in the ESA/NASA standard for satellite transmission, up to $t = 16$ zeros must be found in the field $\rm GF(255)$ to decode a single code word. And this in real time!<br> | |
| − | + | Beginning in the late 1960s, many scientists sought faster decoding algorithms for Reed–Solomon codes: | |
| − | + | # In [https://en.wikipedia.org/wiki/Berlekamp%E2%80%93Massey_algorithm $\text{Berlekamp–Massey algorithm}$] $\rm (BMA)$ the key equation $\underline {\it \Lambda} \cdot \underline{s }^{\rm T} = 0$ represented as a feedback shift register, see for example [Mas69]<ref name ='Mas69'>Massey, J.L.: Shift Register Synthesis and BCH Decoding. IEEE Trans. on Information Theory, vol. IT-15, pp. 122–127, Jan. 1969.</ref>, [Fri96]<ref name ='Fri96'>Friedrichs, B.: Kanalcodierung – Grundlagen und Anwendungen in modernen Kommunikations- systemen. Berlin – Heidelberg: Springer, 1996.</ref>, [Bos99]<ref name ='Bos99'>Bossert, M.: Channel Coding for Telecommunications. Chichester: Wiley, 1999.</ref>. The problem is thus reduced to the synthesis of an autoregressive filter. The algorithm works much faster than the (more easily comprehensible) Petersen algorithm.<br> | |
| + | # Somewhat later, in [SK+75]<ref name='SK+75'>Sugiyama, Y.; Kashara, M.; Hirasawa, S.; Namekawa, T.: A Method for Solving Key Equation for Decoding Goppa Codes. Information and Control, Vol. 27, pp. 87-99, 1975.</ref> a decoding method based on the [https://en.wikipedia.org/wiki/Euclidean_algorithm $\text{Euclidean algorithm}$] has been proposed. This provides the greatest common divisor of two integers, which is used for decoding. The Euclidean algorithm is comparably fast as the $\rm BMA$. More detailed information can be found in [Bos99]<ref name ='Bos99'></ref> and [Fri96]<ref name ='Fri96'></ref>.<br> | ||
| + | # Other efficient decoding methods of Reed–Solomon codes operate in the frequency domain using the [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Arguments_for_the_discrete_implementation_of_the_Fourier_transform|$\text{Discrete Fourier Transform}$]] $\rm (DFT)$ in the field ${\rm GF}(n)$.<br><br> | ||
| − | + | The basic features of Reed–Solomon error correction were already developed in the 1960s. But up to the present time the $($as fast as possible$)$ algebraic decoding of these codes is a highly topical field of research. | |
| − | == | + | == Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.12:_Decoding_at_RSC_(7,_4,_4)_to_Base_8|Exercise 2.12: Decoding at RSC (7, 4, 4) to Base 8]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.12Z:_Reed-Solomon_Syndrome_Calculation|Exercise 2.12Z: Reed-Solomon Syndrome Calculation]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.13:_Decoding_at_RSC_(7,_3,_5)_to_Base_8|Exercise 2.13: Decoding at RSC (7, 3, 5) to Base 8]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.14:_Petersen_Algorithm|Exercise 2.14: Petersen Algorithm]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 13:43, 24 November 2022
Contents
- 1 Block diagram and requirements for RS error correction
- 2 Possible code word estimators for Reed-Solomon decoding
- 3 Bounded Distance Decoding Procedure
- 4 Step (A): Evaluation of the syndrome in BDD
- 5 Error Locator Polynomial - Definition and Properties
- 6 Step (B): Set up/evaluate the ELP coefficient vector
- 7 Step (C): Localization of the error positions
- 8 Step (D): Final error correction
- 9 Fast Reed-Solomon decoding
- 10 Exercises for the chapter
- 11 References
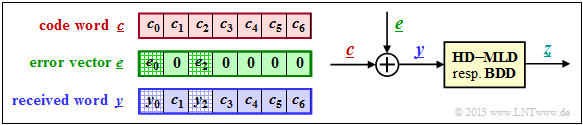
Block diagram and requirements for RS error correction
As in the chapter "Decoding at the Erasure Channel" we consider a transmission system with Reed–Solomon coding characterized by the two code parameters $n=2^m-1$ and $k$. With the generator matrix $\boldsymbol{\rm G}$ the relation between the information word $\underline {u}$ and the code word $\underline {c}$ is:
- $$\underline {c} = {\rm enc}(\underline {u}) = \underline {u} \cdot { \boldsymbol{\rm G}}
\hspace{0.3cm} {\rm with}$$
- $$ \underline {u} = (u_0, u_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_{k-1})\hspace{0.05cm},$$
- $$ \underline {c} = (c_0, c_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_{n-1}) \hspace{0.05cm}.$$
The symbols $u_i$ and $c_i$ originate from the field ${\rm GF}(q)$ with
- $$q=n+1=2^m.$$
They are representable by $m$ binary symbols ("bits").
A comparison of the upper block diagram with the corresponding $\text{block diagram for Reed-Solomon error detection}$ shows:
- The main difference is in the discrete channel model $($highlighted in green$)$. Instead of the erasure channel ("$m$–BEC") now the "$m$–BSC" is considered. For each bit of the code symbol $c_i$ the $\text{Binary Symmetric Channel}$ $\rm (BSC)$ is applied. A bit error with respect to the $i$–th bit of the code word results in $y_i \ne c_i$.
- In the "last chapter" uncertain bits were already marked by erasures $\rm E$. The task of the "code word finder" $\rm (CWF)$ was to reconstruct the decoding result $\underline {y}$ from the garbled received words $\underline {z}$.
- If the number $e$ of erasures is smaller than the minimum distance $d_{\rm min}$, this succeeds and we get $\underline {z} = \underline {c}$. Otherwise, the code word finder reports that it cannot decode the current received word $\underline {y}$ . A wrong decision $(\underline {z} \ne \underline {c})$ was excluded at the BEC.
- In this chapter, the first decoder block is now referred to as "code word estimator" $\rm (CWS)$. The naming is to make clear that due to the $m$–BSC model, wrong decisions $(\underline {z} \ne \underline {c})$ are inevitable, namely when multiple symbol errors distort the received word $\underline {y}$ to a valid code word.
$\text{Conclusions:}$
- The decoder's task is to determine its output vector $\underline {v}$ so that it matches the information word $\underline {u}$ "as well as possible". More precisely formulated:
- \[{ \rm Pr(block\hspace{0.15cm}error)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
- Because of deterministic mapping $\underline{c} = {\rm enc}(\underline{u})$ and $\underline{v} = {\rm enc}^{-1}(\underline{z})$ holds in the same way:
- \[{ \rm Pr(block\hspace{0.15cm}error)} = { \rm Pr}( \underline{z} \ne \underline{c}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
The two blocks highlighted in yellow are not considered further. The focus of the considerations is now the "code word estimator" $\rm (CWS)$ highlighted in red.
Possible code word estimators for Reed-Solomon decoding
The right sketch of this graphic illustrates the task of the $\rm CWS$
- where here the channel model "$m$–BSC" is replaced
- by the additive »error vector«
- $$\underline{e} = \underline{y} - \underline{c}.$$
The sketch on the left illustrates the relationship between these vectors.
This task is to be clarified by an example.
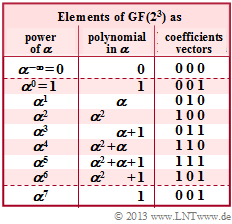
$\text{Example 1:}$ Let all symbols be elements of $\rm GF(2^3) \in \{0,\ 1,\ \alpha^1,\ \alpha^2,\ \alpha^3,\ \alpha^4,\ \alpha^5,\ \alpha^6\}$. The adjacent table can be used for conversion
- between the coefficient representation $($with the order $k_2$, $k_1$, $k_0)$
- and the exponent representation $($as powers of the primitive element $\alpha).$
In this example, the code word and received word are in coefficient notation:
- \[\underline{c} = \Big ( (010), (001), (100),(010),(100),(111),(111)\Big )\hspace{0.05cm},\]
- \[\underline{y} =\Big ( (011), (001), (000),(010),(100),(111),(111)\Big )\hspace{0.05cm}.\]
⇒ This results in the following error vector $\underline{e} = \underline{y} - \underline{c}$:
- \[\underline{e} \hspace{0.05cm} = \hspace{0.05cm} \Big ( (001), (000), (100), (000),(000),(000),(000)\Big )\hspace{0.05cm}.\]
⇒ Converted to the exponential representation, we get:
- \[\underline{c} = \Big ( \alpha^1, \hspace{0.09cm}1\hspace{0.09cm}, \alpha^2,\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big )\hspace{0.05cm},\]
- \[\underline{y} =\Big ( \alpha^3, \hspace{0.09cm}1\hspace{0.09cm}, \hspace{0.09cm}0\hspace{0.09cm},\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big )\hspace{0.05cm},\]
- \[\underline{e} = \Big ( \hspace{0.09cm}1\hspace{0.09cm}, \hspace{0.09cm}0\hspace{0.09cm}, \hspace{0.05cm}\alpha^2,\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm}\Big )\hspace{0.05cm}.\]
Note Task of the code word estimator $\rm (CWS)$ is to find the most probable code word to $\underline{y}$ and to pass its result $\underline{z} = \underline{c}_i$ to the following mapping.
There are several ways to do this:
- Hard Decision Maximum Likelihood Decoding $\text{(HD–MLD)}$,
- Bounded Distance Decoding $\text{(BDD)}$,
- Decoding "over half the minimum distance".
Hard Decision Maximum Likelihood Decoding $\text{(HD–MLD)}$:
One chooses from all possible Reed–Solomon code words $\underline{c}_i$ $($hierof there are in total $q^k)$ the one with the least $\text{Hamming distance}$ to the received word $\underline{y}$. Result:
- \[\underline{z} = {\rm arg} \min_{\underline{c}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}_{\rm RS}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{c}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
- The decision here happens on the maximum inference probability ${\rm Pr}(\underline{c}_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y})$ and leads to the best possible result. For more details see "Maximum-likelihood decision Decision at the BSC Channel".
- A decision is always made even if the number $r$ of symbol errors is larger than the correction capability $t$ of the code. However, in such a case the decoding result is very uncertain.
- It should be mentioned again that maximum likelihood decoding always decides. Decoding failure is impossible. But of course there are also wrong decisions.
Bounded Distance Decoding $\text{(BDD)}$:
If the number $r$ of symbol errors in the received word $\underline{y}$ is not greater than the correction capability $t = ⌊(d_{\rm min}- 1)/2⌋$ of the code, one can correct the $r$ symbol errors completely. However, it is also true:
- The case $r > t$ leads to an abort of the decoding process with no result. In other words:
- Only those received words towards the center of the sphere are decoded, which lie in a sphere around it with radius $t$.
- Other received words are marked as undecodable, for example as "erasure".
- Other received words are marked as undecodable, for example as "erasure".
Decoding over half the minimum distance:
Here also in the case $r > t$ an attempt is made to decode the code word. However, in contrast to $\text{HD–MLD}$, which also decodes beyond half the minimum distance, a decoding failure is not per se excluded here.
- For the remainder of this chapter, we will deal exclusively with "Bounded Distance Decoding". The reason for this is the enormous complexity of "Maximum Likelihood Decoding" proportional to $q^{n-k}$.
Bounded Distance Decoding Procedure
In the following, the individual steps of the "bounded distance decoding" $\rm (BDD)$ algorithm are described briefly and in a recipe-like manner. In the next sections, the individual points will be dealt with in more detail and the procedure will be illustrated using typical examples.
$\rm (A)$ $\text{Calculation and evaluation of syndrome}$ ⇒ $\text{Detailed description}$
- Calculate from the received word $\underline{y}$ and the parity-check matrix $\boldsymbol{\rm H }$ of the code the syndrome $\underline {s} = \underline {y} \cdot \boldsymbol{\rm H }^{\rm T}$.
- If $\underline {s} =\underline {0}$, set the BDD output $\underline {z} =\underline {y}$ and terminate the decoding process for that received word.
- Otherwise, set the parameter $r = 1$ and continue with step $\rm (B)$ .
$\rm (B)$ $\text{Determine the actual symbol error count }\ r$ ⇒ $\text{Detailed description}$
- Create and check the equations $\underline {\it \Lambda} _l \cdot\underline {s}^{\rm T} = 0$ for $l = 1,$ ... , $2 \cdot t -r$ assuming that the received word contains exactly $r$ symbol errors.
- $\underline {\it \Lambda} _l $ denotes the generalized $\text{error locator polynomial}$ $\text{(ELP)}$ coefficient vectors.
- The parameter $t$ denotes the correctability of the code. For the Reed–Solomon codes, uniformly $t = ⌊(n-k)/2 ⌋$.
- If there is a unique solution, then continue with step $\rm (C)$.
In the received vector $\underline{y}$ there are then indeed exactly $r$ symbols falsified and in the error vector $\underline{e}$ there are $r$ entries not equal to $0$. - Otherwise increase $r$ by $1$. If $r ≤ t$ ⇒ repeat step $\rm (B)$ from the beginning:
The previously assumed $r$ was obviously too small. Therefore now a new attempt with larger $r$. - If the new $r$ is greater than the correction capability $t$ of the code, the current word cannot be decoded. End the decoding attempt with an "error message".
$\rm (C)$ $\text{Localization of the }\ r \text{ error locations}$ ⇒ $\text{Detailed description}$
- Create the error locator polynomial ${\it \Lambda}(x)$ and find its $r$ zeros in ${\rm GF}(q) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\}$.
- An error at location $i$ is present whenever ${\it \Lambda}(\alpha^{i}) = 0$ .
$\rm (D)$ $\text{Determination of }\ r \text{ error values and correction}$ ⇒ $\text{Detailed description}$
- Now the $r$ error locations are known. Replacing in the received vector $\underline{y}$ the wrong symbols with erasures ⇒ $y_i = \rm E$, if $e_i ≠ 0$,
we find the result $\underline{y}$ corresponding to the chapter "Reed-Solomon Decoding at the Erasure Channel". - Or: From the equation $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$ one arrives at a linear equation system for the faulty symbols $(e_i \ne 0)$ taking advantage of the error-free sites $(e_i = 0)$.
Step (A): Evaluation of the syndrome in BDD
As shown in section "Principle of Syndrome Decoding", the syndrome $\underline{s}$ can be used to decode a linear code.
- With the received word $\underline{y}$ equal to code word $\underline{c}$ plus error vector $\underline{e}$ applies:
- \[\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}= \underline {c} \cdot { \boldsymbol{\rm H }}^{\rm T}+ \underline {e} \cdot { \boldsymbol{\rm H }}^{\rm T} \hspace{0.05cm}.\]
- Since always $\underline {c} \cdot { \boldsymbol{\rm H }}^{\rm T} =\underline {0}$ holds, it follows from $\underline{s}= \underline{0}$ also $\underline {e} \cdot { \boldsymbol{\rm H }}^{\rm T} =\underline{0}$. That is:
- With very high probability, from $\underline{s}= \underline{0}$ it is also possible to infer $\underline{e}= \underline{0}$ and thus also the correct decoding result $\underline{z}= \underline{y}$. The decoding process would be finished.
- But there are also error patterns $\underline{e} \ne \underline{0}$ that lead to the syndrome $\underline{s}= \underline{0}$. Such patterns certainly contain more than $t$ symbol errors.
- So here it makes also sense to abort the decoding process. All subsequent calculations would also not lead to success.
$\text{Example 2:}$ This and the following examples in the next sections are always based on the Reed–Solomon code $\text{RSC (7, 3, 5)}_8$ so that the conversions given in the graph in $\rm GF(2^3)$ can be used. The received words are:
- \[\underline{y}=\big (\alpha^3,\hspace{0.08cm} 1,\hspace{0.08cm} 0, \hspace{0.08cm}\alpha^1, \hspace{0.08cm} \alpha^2, \hspace{0.08cm} \alpha^5, \hspace{0.08cm} \alpha^5 \big).\]
- With the $\text{parity-check matrix}$ $\boldsymbol{\rm H }$ results for the syndrome:
- \[\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H } }^{\rm T}= \begin{pmatrix} \alpha^3, \hspace{0.05cm}1, \hspace{0.05cm}0, \hspace{0.05cm}\alpha^1, \hspace{0.05cm}\alpha^2, \hspace{0.05cm}\alpha^5, \hspace{0.05cm}\alpha^5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 \\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 \\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^5 \\ \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 \\ \alpha^5 & \alpha^3 & \alpha^1 & \alpha^6 \\ \alpha^6 & \alpha^5 & \alpha^4 & \alpha^3 \end{pmatrix}. \]
- These vector–matrix multiplications gives the result:
- \[\underline {s} \hspace{-0.05cm} = \hspace{-0.05cm} (\alpha^3 , \alpha^3 , \alpha^3 , \alpha^3) + (\alpha^1 , \alpha^2 , \alpha^3 , \alpha^4) + (0,0,0,0) \hspace{-0.05cm}+\hspace{-0.05cm} (\alpha^4,1,\alpha^3,\alpha^6)+(\alpha^6,\alpha^3,1,\alpha^4)\hspace{-0.05cm}+\hspace{-0.05cm}(\alpha^3,\alpha^1,\alpha^6,\alpha^4) \hspace{-0.05cm}+\hspace{-0.05cm} (\alpha^4,\alpha^3,\alpha^2,\alpha^1)\]
- \[\Rightarrow \hspace{0.3cm} \underline {s} = \text{...} \hspace{0.05cm}= (\alpha^5,\alpha^2,\alpha^3,\alpha^1) \hspace{0.05cm}.\]
- So the received word was falsified. Otherwise it should have resulted in $\underline{e}= \underline{0} = (0, 0, 0, 0)$ .
The description of the decoding process at $\text{RSC (7, 3, 5)}_8$ is continued in $\text{Example 4}$
Error Locator Polynomial - Definition and Properties
After the syndrome calculation in step $\rm (A)$ with the result $\underline{s} \ne \underline{0}$ we know,
- that the received word $\underline{y}$ does not match the code word $\underline{c}$, respectively
- that the error vector $\underline{e} = (e_0, \hspace{0.05cm}e_1, \hspace{0.05cm}\text{ ...}\hspace{0.05cm} , e_{n-1})$ certainly includes elements not equal to "$0$".
However, we do not know how many symbols were falsified $(0 < r ≤ n)$ nor we can name the positions of the error locations $(e_i ≠ 0)$ in the error vector $\underline{c}$. An approach to this task is provided by the so-called "error locator polynomial" introduced by $\text{William Wesley Peterson}$ ⇒ see [Pet60][1]. It is also known as "key equation".
$\text{Definition:}$ Let it be known that exactly $r$ elements of the error vector $\underline{e}$ are non-zero, recognizable by $\text{Hamming weight}$ $w_{\rm H}(\underline{e}) = r$.
- Also let the quantity ${I}_{\rm EP}$ of error positions be known:
- \[I_{\rm EP} = \{ i \hspace{0.1cm}\vert \hspace{0.1cm} e_i \ne 0,\hspace{0.1cm} 0 \le i < n \}\hspace{0.05cm}.\]
- Then for the »Error Locator Polynomial« $\rm (ELP)$:
- \[{\it \Lambda}(x)=x \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm FP} }(x-\alpha^i) =x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ].\]
⇒ From the error locator polynomial we know:
- Because of the factor $x$ in front of the product sign: ${\it \Lambda}(x= 0) = 0$.
- Other $r$ zeros result for $x = \alpha^{i}$ with $i \in I_{\rm EP}$, that is, for all error positions.
- In contrast, the error locator polynomial for $i ∉ I_{\rm EP}$ ⇒ $e_i = 0$ has no zero: ${\it \Lambda}(x= \alpha^{i}) \ne0$.
⇒ So we search for the $r$ non–trivial zeros of ${\it \Lambda}(x)$ with argument $x ∈ {\rm GF}(q) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\}$. If we succeed,
- we know the $r$ error positions,
- but not yet the actual error values $e_i ∈ {\rm GF}(q)$.
$\text{Example 3:}$
Let $n=7$ ⇒ $q=8$, $r=2$ and $I_{\rm FP} = \{2, \hspace{0.05cm}4\}$: ![]()
- Thus for the "error locator poynomial" from ${\rm GF}(2^3)$ is obtained:
- \[{\it \Lambda}(x)=x \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^4)= x \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^4) =x \cdot \big [x^2 \hspace{-0.05cm}+ \hspace{-0.05cm}(\alpha^2 + \alpha^4) \cdot x + \alpha^6\big ] \]
- \[\Rightarrow \hspace{0.3cm} {\it \Lambda}(x)= x \cdot \big [\alpha^6 + \alpha \cdot x + x^2\big ]\hspace{0.05cm}.\]
- The other zeros $($except for $x = 0)$ arise naturally here for $x = \alpha^2$ and $x = \alpha^4$, as a calculation shows:
- \[{\it \Lambda}(x = \alpha^2)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^2 + (\alpha^2)^2\big ] = x \cdot \big [\alpha^6 + \alpha^3 + \alpha^4 \big ]= 0\hspace{0.05cm},\]
- \[ {\it \Lambda}(x = \alpha^4)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^4 + (\alpha^4)^2\big ] =x \cdot \big [\alpha^6 + \alpha^5 + \alpha \big ]= 0\hspace{0.05cm}.\]
For further derivation, we always assume the $\text{RSC (7, 3, 5)}_8$ with the following parameter values:
- $$n=7, \hspace{0.3cm}k = 3, \hspace{0.3cm}d_{\rm min} = 5 \ \Rightarrow \ t = (d_{\rm min} -1/2) = 2.$$
- Let the number of symbol errors be $r = t = 2$. Thus the system of equations to be solved with the auxiliary variables $L_i = {\it \Lambda}(\alpha^{i})$:
- \[L_0 = {\it \Lambda }(\alpha^0) = \alpha^0 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^0)^1 + (\alpha^0)^2 \right ] = {\it \lambda}_0 \cdot 1 + {\it \lambda}_1 \cdot 1 + 1 \hspace{0.05cm},\]
- \[L_1 = {\it \Lambda }(\alpha^1) =\alpha^1 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^1)^1 + (\alpha^1)^2 \right ] = {\it \lambda}_0 \cdot \alpha^1+ {\it \lambda}_1 \cdot \alpha^2 + \alpha^3 \hspace{0.05cm},\]
- \[...\]
- \[ L_6 = {\it \Lambda }(\alpha^6) = \alpha^6 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^6)^1 + (\alpha^6)^2 \right ] = {\it \lambda}_0 \cdot \alpha^6 + {\it \lambda}_1 \cdot \alpha^{12} + \alpha^{18} \hspace{0.05cm}.\]
- In vector form, this system of equations with the auxiliary vector is $\underline{L} = (L_0, \hspace{0.05cm}L_1, \hspace{0.05cm}L_2,\hspace{0.05cm}L_3,\hspace{0.05cm}L_4,\hspace{0.05cm}L_5,\hspace{0.05cm}L_6)$:
- \[\underline {L}^{\rm T}=\begin{pmatrix} L_0\\ L_1\\ L_2\\ L_3\\ L_4\\ L_5\\ L_6 \end{pmatrix} \hspace{0.15cm} = \hspace{0.15cm} \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^9 \\ \alpha^4 & \alpha^8 & \alpha^{12}\\ \alpha^5 & \alpha^{10} & \alpha^{15}\\ \alpha^6 & \alpha^{12} & \alpha^{18} \end{pmatrix} \hspace{0.15cm}\cdot \hspace{0.15cm} \begin{pmatrix} {\lambda}_0\\ {\lambda}_1\\ 1 \end{pmatrix} \hspace{0.05cm}.\]
- We now expand the ELP coefficient vector $\underline {\it \Lambda }$ by appending zeros to the length $n-k$. Thus, in the considered example, we obtain ${\it \Lambda } = ( \lambda_0,\hspace{0.05cm}\lambda_1,\hspace{0.05cm}1, \hspace{0.05cm}0)$ and the following vector equation:
- \[\underline {L}^{\rm T} \hspace{0.15cm} = \hspace{0.15cm} \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^8\\ \alpha^3 & \alpha^6 & \alpha^9 & \alpha^{12}\\ \alpha^4 & \alpha^8 & \alpha^{12} & \alpha^{16}\\ \alpha^5 & \alpha^{10} & \alpha^{15} & \alpha^{20}\\ \alpha^6 & \alpha^{12} & \alpha^{18} & \alpha^{24} \end{pmatrix} \hspace{0.15cm}\cdot \hspace{0.15cm} \begin{pmatrix} {\lambda}_0\\ {\lambda}_1\\ 1\\ 0 \end{pmatrix} \hspace{0.05cm}.\]
- With this we have achieved:
- The $7× 3$ matrix has now become a $7× 4$ matrix.
- The fourth column can actually be filled arbitrarily, since all elements are multiplied by zeros.
- The addition chosen here gives the transposed $\text{parity-check matrix}$ of $\text{RSC (7, 3, 5)}_8$.
- Thus, one can write for the last vector equation:
- \[\underline {L}^{\rm T} = { \boldsymbol{\rm H }}^{\rm T} \cdot \underline {\it \Lambda }^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline {L} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \hspace{0.05cm}.\]
- But since for the error locations $(e_i ≠ 0)$ always $L_i = {\it \Lambda}(\alpha^{i}) = 0$ holds, the product $L_i \cdot e_i \equiv 0$ and one obtains as determining equation for the zeros of the error locator polynomial:
- \[\underline {L}^{\rm T} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 \hspace{0.05cm}.\]
$\text{Important intermediate result:}$ The non-trivial zeros $\lambda_0$, $\lambda_1$, ... $(=0)$ of the error locator polynomial ${\it \Lambda}(x)$ must always satisfy the vector equation $\underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 $ .
- Hereby denotes $\underline {\it \Lambda }$ the $\rm ELP$ coefficient vector.
- $\underline {s } = \underline {y }\cdot \boldsymbol{\rm H }^{\rm T} $ gives the $\text{syndrome}$.
Step (B): Set up/evaluate the ELP coefficient vector
Before we can consider this intermediate result for step $\rm (B)$ some generalizations need to be made.
The reason for this is:
- The relationship $\underline {\it \lambda } \cdot \underline {s}^{\rm T} = 0 $ yields only a single equation of determination.
- Thus the problem can be solved for $r = 1$ if one is sure that indeed only one symbol has been falsified.
- If one is not sure of this, but nevertheless performs the calculation for $r = 1$, one still needs a second equation (or even several) to verify the assumption.
The property of the $\text{error locator polynomial}$ that ${\it \Lambda}(\alpha^{i}) = 0$ only for $e_i ≠ 0$ $($that means: the $i$–th symbol is falsified$)$ is preserved when multiplying ${\it \Lambda}(x)$ by arbitrary powers of $x$.
Each multiplication by $x$ implies a shift of one place to the right for the ELP coefficient vector.
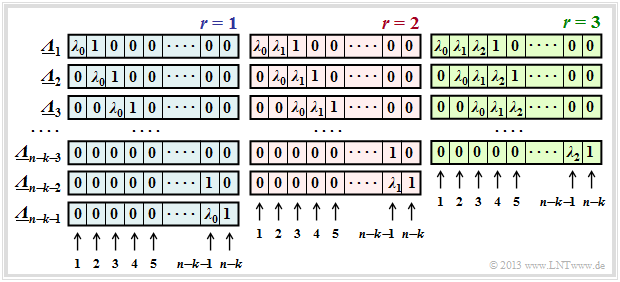
$\text{Definition:}$ The $\text{generalized ELP coefficient vectors}$ $\underline {\it \Lambda }_l$ result from successive shifts with respect to $\underline {\it \Lambda }_l$:
- \[{\it \Lambda}_l(x)=x^l \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm EP} }(x-\alpha^i) =x^l \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ]\hspace{0.05cm}.\]
In this defining equation, $\underline {\it \Lambda }_1$ corresponds to the previous $\underline {\it \Lambda }$.
The upper graph shows the occupancy under the assumption of $r$ error locations in the error vector $\underline {e}$ for
- $r=1$ in the left panel (with blue background),
- $r=2$ in the middle area (with red background),
- $r=3$ in the right area (with green background).
One recognizes:
- The length of all $\underline {\it \lambda }_l$ is always $n-k$. Each vector contains respectively $r$ coefficients $\lambda_0$, $\lambda_1$, ... , $\lambda_{r-1}$ ⇒ $0 ≤ i < r$ and one "1".
The remainder of each vector is padded with zeros. - For each $r$ there are exactly $n-k-r$ coefficient vectors $\underline {\it \Lambda }_l$, where $\underline {\it \Lambda }_l$ results from $\underline {\it \Lambda }_{l-1} $ always by right shifting by one position.
The vector $\underline {\it \Lambda }_{n-k-r}$ always ends with a $1$. - The equation system $\underline {\it \Lambda }_l \cdot \underline {s}^{\rm T} = 0 $ therefore leads to $n-k-r$ equations.
The chosen approach for $r$ is only correct if all equations lead to the same results for $\lambda_0$, ... , $\lambda_{r-1}$ . - If this is not the case, one has to increase $r$ and thus work on a new equation system, and this until a unique solution results from all equations for the current $r$. If the finally $r$ is greater than the correctability $t$ of the code, the calculation can be terminated. The pending received word $\underline {y}$ is then not decodable.
$\text{Example 4:}$ The conditions stated in the $\text{Example 2}$ still apply:
- There, due to the syndrome $\underline {s} = (\alpha^5,\ \alpha^2,\ \alpha^3,\ \alpha^1) ≠ \underline {0}$ it was also demonstrated that the received vector $\underline {y}$ was falsified ⇒ error vector $\underline {e} \ne {0}$.
- Not known, however, is the actual symbol error count $r$.
- Assuming a single falsified symbol $(r= 1)$ we obtain the following system of equations $($written here in matrix form$)$:
- \[\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= \begin{pmatrix} \lambda_0 & 1 & 0 & 0 \\ 0 & \lambda_0 & 1 & 0 \\ 0 & 0 & \lambda_0 & 1 \end{pmatrix} \cdot \begin{pmatrix} \alpha^5\\ \alpha^2\\ \alpha^3\\ \alpha \end{pmatrix} \stackrel{!}{=} \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \hspace{0.05cm}.\]
- This equation system gives three different solutions for $\lambda_0$, which is not purposeful:
- \[\text{line 1:}\hspace{0.5cm}\alpha^5 \cdot \lambda_0 + \alpha^2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{2-5}= \alpha^{-3}= \alpha^{4}\hspace{0.05cm},\]
- \[\text{line 2:}\hspace{0.5cm}\alpha^2 \cdot \lambda_0 + \alpha^3 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{3-2}= \alpha\hspace{0.05cm},\]
- \[\text{line 3:}\hspace{0.5cm}\alpha^3 \cdot \lambda_0 + \alpha^1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{1-3}= \alpha^{-2} = \alpha^{5} \hspace{0.05cm}.\]
- Therefore, we now set up another equation system, assuming $r = 2$:
- \[\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= \begin{pmatrix} \lambda_0 & \lambda_1 & 1 & 0 \\ 0 & \lambda_0 & \lambda_1 & 1 \end{pmatrix} \cdot \begin{pmatrix} \alpha^5\\ \alpha^2\\ \alpha^3\\ \alpha \end{pmatrix} \stackrel{!}{=} \begin{pmatrix} 0\\ 0 \end{pmatrix}\hspace{0.05cm}. \]
- This leads to two equations for $\lambda_0$ and $\lambda_1$:
- \[\alpha^5 \cdot \lambda_0 + \alpha^2 \cdot \lambda_1 + \alpha^3 = 0 \hspace{0.05cm},\hspace{0.5cm}\alpha^2 \cdot \lambda_0 + \alpha^3 \cdot \lambda_1 + \alpha^1 = 0 \hspace{0.05cm}.\]
- This equation system is now clearly solvable. One gets $\lambda_0 = \alpha^2$ and $\lambda_1 = \alpha^6$. This means:
- The assumption that indeed $r = 2$ positions of the received vector $\underline {y}$ have been distorted is correct.
- But it is not yet known which positions have been falsified. So much for now:
- It is not symbol positions 2 and 6, but the positions 0 and 2, as shown in the following $\text{Example 5}$ (next section).
Step (C): Localization of the error positions
After processing step $\rm(B)$ are known:
- the number $r$ of error locations $e_i ≠ 0$ in the vector $\underline {e} = (e_0, \hspace{0.05cm}\text{... }\hspace{0.05cm}, e_i, \hspace{0.05cm}\text{... }\hspace{0.05cm}, e_{n-1})$,
- the coefficients $\lambda_0, \hspace{0.05cm}\text{... }\hspace{0.05cm} , \lambda_{r-1}$ of the error locator polynomial..
Now the set of error positions has to be determined: $I_{\rm EP} = \{ i \hspace{0.1cm}| \hspace{0.1cm} e_i \ne 0,\hspace{0.3cm} 0 \le i < n \}\hspace{0.05cm}.$
There are two ways to do this $($both methods are used in the following example$)$:
- the so-called "Chien search", in which one determines the searched zeros by inserting the possible code symbols except the zero symbol ⇒ $(\alpha^0, \text{... }, \alpha^i, \text{... },\alpha^{n-1})$ into the the error locator polynomial,
- the evaluation of the equation $\underline {L} = (L_0, \text{... }, L_i, \text{... },L_{n-1} ) = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }}$ with the abbreviation $L_i = {\it \Lambda}(\alpha^i)$.
$\text{Example 5:}$ In $\text{Example 4}$ it was determined according to the constraints specified in $\text{Example 2}$ stated boundary conditions determined that
- $r= 2$ symbol errors are present, and
- the ELP coefficients are $\lambda_0 = \alpha^2$ and $\lambda_1 = \alpha^6$.
This results in the following error locator polynomial:
- \[{\it \Lambda}(x)=x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+x^2 \big ] =x \cdot \big [\alpha^2 + \alpha^6 \cdot x+x^2 \big ]\hspace{0.05cm}.\]
⇒ According to the Chien search one gets
- \[{\it \Lambda}(\alpha^0)\hspace{0.15cm} = \hspace{0.15cm}\alpha^0 \cdot \big [ \alpha^2 + \alpha^6 \cdot 1 + 1 \big ] = \alpha^2 + (\alpha^2 + 1) + 1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zero} }\hspace{0.05cm},\]
- \[{\it \Lambda}(\alpha^1)\hspace{0.15cm} = \hspace{0.15cm}\alpha^1 \cdot \big [\alpha^2 + \alpha^6 \cdot \alpha^1 + \alpha^2\big ]= \alpha^1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm No\hspace{0.15cm} zero}\hspace{0.05cm},\]
- \[{\it \Lambda}(\alpha^2)\hspace{0.15cm} = \hspace{0.15cm}\alpha^2 \cdot \big [ \alpha^2 + \alpha^6 \cdot \alpha^2 + \alpha^4 \big ] =\alpha^4 + \alpha^{10} + \alpha^6 = \text{...} = \hspace{0.15cm}0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zero} }\hspace{0.05cm}.\]
Thus the two error positions with $i = 0$ and $i = 2$ are found ⇒ the error vector is: $\underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)$ .
⇒ The vector equation $\underline {L} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H } }$ gives the same result in a more compact form:
- \[\underline {L} = \underline{\it \Lambda} \cdot { \boldsymbol{\rm H } } = (\alpha^2, \alpha^6, 1, 0) \cdot \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6 \\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^3 & \alpha^5 \\ 1 & \alpha^3 & \alpha^6 & \alpha^3 & \alpha^5 & \alpha^1 & \alpha^4 \\ 1 & \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 & \alpha^6 & \alpha^3 \end{pmatrix} \]
- \[ \Rightarrow \hspace{0.3cm} \underline {L} = (\alpha^2,\alpha^3,\alpha^4,\alpha^5,\alpha^6,1 ,\alpha^1) + (\alpha^6,\alpha^1,\alpha^3,\alpha^5,1 ,\alpha^2,\alpha^4)+(1, \alpha^3,\alpha^6,\alpha^3,\alpha^5,\alpha^1,\alpha^4) \]
- \[ \Rightarrow \hspace{0.3cm} \underline {L} = (0,\alpha^1,0,\alpha^3,\alpha^3,\alpha^5,\alpha^1)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} L_0 = L_2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)\hspace{0.05cm}.\]
The example continues with the $\text{Example 6}$ in the next section
.
Step (D): Final error correction
In the last step the $r$ symbol errors have to be corrected, whose positions are known after completion of step $\rm (C)$ :
- Marking the error positions in the received word $\underline {y}$ as erasures $\rm E$, the corresponding code word $\underline {z}$ can be found according to the description in chapter "Reed-Solomon decoding at the erasure channel".
- A second possibility offers the determination of the error vector $\underline {e}$ from the equation $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$ and correcting accordingly $\underline {z} = \underline {y} - \underline {e} $. This procedure is the basis of the following example.
$\text{Example 6:}$ We consider again the $\text{RSC (7, 3, 5)}_8$. In $\text{Example 2}$ was
- the received word given with $\underline{y}=\big (\alpha^3,\hspace{0.09cm} 1,\hspace{0.09cm} 0, \hspace{0.09cm}\alpha^1, \hspace{0.09cm} \alpha^2, \hspace{0.09cm} \alpha^5, \hspace{0.09cm} \alpha^5 \big),$ and
- from this determined the syndrome $\underline{s}=\big (\alpha^5,\hspace{0.09cm}\alpha^2, \hspace{0.09cm} \alpha^3, \hspace{0.09cm} \alpha^1\big)$.
According to the calculations in $\text{Example 5}$ the error vector is $\underline {e} = (e_0,\ 0,\ e_2,\ 0,\ 0,\ 0,\ 0)$.
From $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$ we now obtain the following governing equations for the error values $e_0$ and $e_2$:
- \[\underline {e} \cdot \boldsymbol{\rm H }^{\rm T}= \begin{pmatrix} e_0 & 0 & e_2 & 0 & 0 & 0 & 0 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5}\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2}\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^{6}\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^{3} \end{pmatrix} \stackrel{!}{=} \underline {s} = \begin{pmatrix} \alpha^5 & \alpha^2 & \alpha^3 & \alpha^1 \end{pmatrix} \]
- \[\Rightarrow \hspace{0.3cm}e_0 \cdot (1,\ 1,\ 1,\ 1) + e_2 \cdot (\alpha^2,\ \alpha^4,\ \alpha^6,\ \alpha^1)\stackrel{!}{=} ( \alpha^5,\ \alpha^2,\ \alpha^3,\ \alpha^1)\]
- \[\Rightarrow \hspace{0.3cm} e_0 + e_2 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^4 = \alpha^2\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^6 = \alpha^3\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^1 = \alpha^1\hspace{0.05cm}.\]
- All equations lead to the result $e_0 = 1$ and $e_2 =\alpha^2$.
- Thus the corrected code word with $\underline {y} = (\alpha^3,\hspace{0.09cm} 1,\hspace{0.09cm} 0,\hspace{0.09cm} \alpha^1,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} \alpha^5,\hspace{0.09cm} \alpha^5)$ and $\underline {e}= (1,\hspace{0.09cm} 0,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} 0,\hspace{0.09cm} 0,\hspace{0.09cm} 0,\hspace{0.09cm} 0)$:
- \[\underline {z} = \underline {y} - \underline {e} = \underline {y} + \underline {e}= (\alpha^1,\hspace{0.09cm} 1,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} \alpha^1,\hspace{0.09cm} \alpha^2,\hspace{0.09cm} \alpha^5,\hspace{0.09cm} \alpha^5)\hspace{0.05cm}. \]
- This is a valid code word of the $\text{RSC (7, 3, 5)}_8$.
Fast Reed-Solomon decoding
The class of Reed–Solomon codes was already introduced in 1960 by the publication [RS60][2]. However, their efficient decoding was not possible until a decade or two later.
In the last sections we have demonstrated the so-called "Petersen algorithm" including the "Chien search" on the example of $\text{RSC (7, 3, 5)}_8$ which can correct up to $t = 2$ errors.
- The decoding process focused on setting up and solving the key equation where the zeros of a degree-2 polynomial in the field $\rm GF(7)$ had to be found.
- It was to be recognized that already this algebraic decoding is connected with large expenditure.
For codes used in practice with large code word length $n$ and high correctability $t$ the decoding effort would explode if faster decoding algorithms had not been found.
- For example, in the Reed–Solomon code $\text{RSC (255, 223, 33)}_{256}$, mentioned early in the ESA/NASA standard for satellite transmission, up to $t = 16$ zeros must be found in the field $\rm GF(255)$ to decode a single code word. And this in real time!
Beginning in the late 1960s, many scientists sought faster decoding algorithms for Reed–Solomon codes:
- In $\text{Berlekamp–Massey algorithm}$ $\rm (BMA)$ the key equation $\underline {\it \Lambda} \cdot \underline{s }^{\rm T} = 0$ represented as a feedback shift register, see for example [Mas69][3], [Fri96][4], [Bos99][5]. The problem is thus reduced to the synthesis of an autoregressive filter. The algorithm works much faster than the (more easily comprehensible) Petersen algorithm.
- Somewhat later, in [SK+75][6] a decoding method based on the $\text{Euclidean algorithm}$ has been proposed. This provides the greatest common divisor of two integers, which is used for decoding. The Euclidean algorithm is comparably fast as the $\rm BMA$. More detailed information can be found in [Bos99][5] and [Fri96][4].
- Other efficient decoding methods of Reed–Solomon codes operate in the frequency domain using the $\text{Discrete Fourier Transform}$ $\rm (DFT)$ in the field ${\rm GF}(n)$.
The basic features of Reed–Solomon error correction were already developed in the 1960s. But up to the present time the $($as fast as possible$)$ algebraic decoding of these codes is a highly topical field of research.
Exercises for the chapter
Exercise 2.12: Decoding at RSC (7, 4, 4) to Base 8
Exercise 2.12Z: Reed-Solomon Syndrome Calculation
Exercise 2.13: Decoding at RSC (7, 3, 5) to Base 8
Exercise 2.14: Petersen Algorithm
References
- ↑ Peterson, W.W: Encoding and Error-correction Procedures for the Bose-Chaudhuri codes. IRE Transactions on Information Theory, IT-6:459{470), 1960.
- ↑ Reed, I.S.; Solomon, G.: Polynomial Codes over Certain Finite Fields. J. Siam, Vol. 8, pp. 300-304, 1960.
- ↑ Massey, J.L.: Shift Register Synthesis and BCH Decoding. IEEE Trans. on Information Theory, vol. IT-15, pp. 122–127, Jan. 1969.
- ↑ 4.0 4.1 Friedrichs, B.: Kanalcodierung – Grundlagen und Anwendungen in modernen Kommunikations- systemen. Berlin – Heidelberg: Springer, 1996.
- ↑ 5.0 5.1 Bossert, M.: Channel Coding for Telecommunications. Chichester: Wiley, 1999.
- ↑ Sugiyama, Y.; Kashara, M.; Hirasawa, S.; Namekawa, T.: A Method for Solving Key Equation for Decoding Goppa Codes. Information and Control, Vol. 27, pp. 87-99, 1975.