Difference between revisions of "Channel Coding/Error Probability and Application Areas"
m (Text replacement - "„" to """) |
|||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü=Reed–Solomon–Codes | + | |Untermenü=Reed–Solomon–Codes and Their Decoding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Error Correction According to Reed-Solomon Coding |
| − | |Nächste Seite= | + | |Nächste Seite=Basics of Convolutional Coding |
}} | }} | ||
| − | == | + | == Block error probability for RSC and BDD == |
<br> | <br> | ||
| − | + | For error probability calculation we start from the same block diagram as in chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding| "Error correction according to Reed-Solomon coding"]] , but here we choose the codeword estimator $(\underline {y} → \underline {z})$ to [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Possible_code_word_estimators_for_RS_decoding| "Bounded Distance Decoding"]] $\rm (BDD)$ . For <i>Maximum Likelihood Decoding</i> the results are slightly better.<br> | |
| − | [[File:P ID2564 KC T 2 6 S1 v2.png|center|frame| | + | [[File:P ID2564 KC T 2 6 S1 v2.png|center|frame|System model with Reed–Solomon coding, $m$ BSC and ''Bounded Distance Decoding''|class=fit]] |
| − | + | Let the block error probability be defined as follows: | |
| − | ::<math>{ \rm Pr( | + | ::<math>{ \rm Pr(Block\:error)} = { \rm Pr}( \underline{v} \ne \underline{u})= { \rm Pr}( \underline{z} \ne \underline{c}) = { \rm Pr}( f >t) \hspace{0.05cm}.</math> |
| − | + | Due to the BDD assumption, the same simple result is obtained as for the binary block codes, namely the probability that the number $f$ of errors in the block (received word) is greater than the correctability $t$ of the code. | |
| − | + | Since for the random variable $f$ (number of errors) there is a [[Theory_of_Stochastic_Signals/Binomial_Distribution#Probabilities_of_the_binomial_distribution| "Binomial distribution"]] in the range $0 ≤ f ≤ n$ we obtain: | |
| − | ::<math>{\rm Pr( | + | ::<math>{\rm Pr(Block\:error)} = |
\sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.</math> | \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.</math> | ||
| − | + | But while in the first main chapter always $c_i ∈ \rm GF(2)$ has applied and thus the $f$ transmission errors were in each case bit errors, in Reed– Solomon coding under a transmission error $(y_i \ne c_i)$ because of $c_i ∈ {\rm GF}(2^m)$ and $y_i ∈ {\rm GF}(2^m)$ a <i>symbol error</i>. | |
| − | + | This results in the following differences: | |
| − | * | + | *The discrete channel model used to describe the binary block codes is the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC| "Binary Symmetric Channel"]] (BSC). Each bit $c_i$ of a codeword is corrupted with probability $\varepsilon$ and correctly transmitted with probability $1-\varepsilon$ $(y_i = c_i)$.<br> |
| − | * | + | *For Reed–Solomon–coding, one must replace the BSC model with the $m$ BSC channel model. A symbol $c_i$ is corrupted with probability $\varepsilon_{\rm S}$ into another symbol $y_i$ (no matter which one) and arrives with probability $1-\varepsilon_{\rm S}$ uncorrupted at the receiver.<br><br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | We start from the BSC parameter $\varepsilon = 0.1$ and consider Reed–Solomon code symbols $c_i ∈ {\rm GF}(2^8)$ ⇒ $m = 8$, $q = 256$, $n = 255$. | |
| − | + | For a symbol corruption $(y_i \ne c_i)$ already one wrong bit is sufficient. Or expressed differently: If $y_i = c_i$ is to be valid, then all $m = 8$ bits of the code symbol must be transmitted correctly: | |
::<math>1 - \varepsilon_{\rm S} = (1 - \varepsilon)^m = 0.9^8 \approx 0.43 | ::<math>1 - \varepsilon_{\rm S} = (1 - \varepsilon)^m = 0.9^8 \approx 0.43 | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *Thus, for the 8 BSC model, the falsification probability $\varepsilon_{\rm S} ≈ 0.57$. |
| − | * | + | *With the further assumption that the falsification of $c_i = \beta$ into any other symbol $y_i = \gamma \ne \beta$ is equally likely, we obtain: |
:$${\rm Pr}(y_i = \gamma\hspace{0.05cm}\vert \hspace{0.05cm}c_i = \beta = 0.57/255 ≈ 0.223\%.$$}}<br> | :$${\rm Pr}(y_i = \gamma\hspace{0.05cm}\vert \hspace{0.05cm}c_i = \beta = 0.57/255 ≈ 0.223\%.$$}}<br> | ||
| − | == | + | == Application of Reed–Solomon coding for binary channels == |
<br> | <br> | ||
| − | + | The prerequisites for the following calculation of the block error probability of a system with Reed–Solomon coding and conversion to binary symbols are summarized in the diagram: | |
| − | * | + | *Assume a $(n, k)$ Reed–Solomon coding with symbols of $c_i ∈ {\rm GF}(2^m)$. The smaller the code rate $R=k/m$ is, the less information can be transmitted at a fixed data rate.<br> |
| − | * | + | *Each symbol is represented by $m$ bits in binary ⇒ <i>binary mapping</i>. A block $($code word $\underline {c} )$ thus consists of $n$ symbols or of $n \cdot m$ binary characters (bits) combined in $\underline {c}_{\rm bin} $ .<br> |
| − | * | + | *In addition, the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_Binary_Input |"AWGN Channel"]], identified by the parameter $E_{\rm B}/N_0 $ is assumed. According to this channel model the transmission happens bipolar: "0" ↔ $+1$ and "1" ↔ $-1$. |
| − | * | + | *The receiver makes hard decisions on bit level. Before decoding including error correction, the binary symbols are converted back to ${\rm GF}(2^m)$ symbols.<br> |
| − | [[File:P ID2565 KC T 2 6 S2a v2.png|right|frame| | + | [[File:P ID2565 KC T 2 6 S2a v2.png|right|frame|Application of Reed-Solomon coding for binary channels|class=fit]] |
| − | + | The equation given on the last page (valid for <i>Bounded Distance Decoding</i>), | |
| − | ::<math>{\rm Pr( | + | ::<math>{\rm Pr(Block\:error)} = |
\sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm},</math> | \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm},</math> | ||
| − | + | is based on the $m$ BSC channel. Starting from the AWGN–channel (''Additive White Gaussian Noise ''), the [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Exceedance_probability|"complementary Gaussian error integral"]] ${\rm Q}(x)$ to the BSC parameter | |
| − | |||
::<math>\varepsilon = {\rm Q} \big (\sqrt{2 \cdot E_{\rm S}/N_0} \big ) | ::<math>\varepsilon = {\rm Q} \big (\sqrt{2 \cdot E_{\rm S}/N_0} \big ) | ||
| Line 67: | Line 66: | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | + | comes from this to the symbol-level corruption probability $\varepsilon_{\rm S}$: | |
::<math>\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m | ::<math>\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m | ||
| Line 73: | Line 72: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ One gets with |
* $R=k/n = 239/255 = 0.9373$, | * $R=k/n = 239/255 = 0.9373$, | ||
* $10 \cdot \lg \ E_{\rm B}/N_0 = 7 \, \rm dB$ ⇒ $E_{\rm B}/N_0 ≈ 5$, und | * $10 \cdot \lg \ E_{\rm B}/N_0 = 7 \, \rm dB$ ⇒ $E_{\rm B}/N_0 ≈ 5$, und | ||
| Line 79: | Line 78: | ||
| − | + | for the parameters $\varepsilon$ of the BSC model and $\varepsilon_{\rm S}$ of the 8 BSC model the following numerical values: | |
:$$\varepsilon = {\rm Q} \big (\sqrt{2 \cdot 0.9373 \cdot 5} \big ) = {\rm Q} \big (3.06\big ) \approx 1.1 \cdot 10^{-3}=0.11 \cdot \%$$ | :$$\varepsilon = {\rm Q} \big (\sqrt{2 \cdot 0.9373 \cdot 5} \big ) = {\rm Q} \big (3.06\big ) \approx 1.1 \cdot 10^{-3}=0.11 \cdot \%$$ | ||
| Line 86: | Line 85: | ||
\hspace{0.2cm}(\approx 8 \cdot \varepsilon)\hspace{0.05cm}.$$ | \hspace{0.2cm}(\approx 8 \cdot \varepsilon)\hspace{0.05cm}.$$ | ||
| − | + | So every single symbol is transmitted with more than $99$ percent probability without errors.}}<br> | |
| − | == BER | + | == BER of Reed–Solomon coding for binary channels == |
<br> | <br> | ||
| − | + | The following graph shows the block error probabilities given in [Liv10]<ref name='Liv10'>Liva, G.: ''Channel Coding.'' Lecture Notes, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2010.</ref> given block error probabilities as a function of the AWGN quotient $10 \cdot \lg \ E_{\rm B}/N_0$. | |
| − | [[File:P ID2566 KC T 2 6 S2b v1.png|righr|frame| | + | [[File:P ID2566 KC T 2 6 S2b v1.png|righr|frame|Block error probability of two Reed-Solomon codes of length $n = 255$|class=fit]] |
| − | + | Shown are the calculated curves ${ \rm Pr}( \underline{v} \ne \underline{u})$ for two different Reed–Solomon–codes corresponding to the <i>Deep Space Standards</i> according to CCSDS (<i>Consultative Committee for Space Data Systems</i>), namely | |
| − | * | + | *the $\text{RSC (255, 239, 17)}_{256}$ with $R=0.9373$, which can correct up to $t = 8$ errors, and<br> |
| − | * | + | *the $\text{RSC (255, 223, 33)}_{256}$ with higher correction capability $(t = 16)$ due to smaller code rate. |
| − | + | Hint: Die nachfolgend nur angedeutete Berechnung sollen Sie in der [[Aufgaben:Aufgabe_2.15:_RS-Blockfehlerwahrscheinlichkeit_bei_AWGN|Aufgabe 2.15]] für den $\text{RSC (7, 3, 5)}_{8}$ – also für etwas übersichtlichere Parameter – vollständig durchführen. | |
<br clear=all> | <br clear=all> | ||
Wir analysieren den in der Grafik gelb hinterlegten Punkt, gültig für den $\text{RSC (255, 239, 17)}_{256}$ und $10 \cdot \lg \ E_{\rm B}/N_0 = 7.1 \,\rm dB$ ⇒ $\varepsilon = 0.007$. Die dazugehörige Blockfehlerwahrscheinlichkeit ergibt sich entsprechend der Grafik zu | Wir analysieren den in der Grafik gelb hinterlegten Punkt, gültig für den $\text{RSC (255, 239, 17)}_{256}$ und $10 \cdot \lg \ E_{\rm B}/N_0 = 7.1 \,\rm dB$ ⇒ $\varepsilon = 0.007$. Die dazugehörige Blockfehlerwahrscheinlichkeit ergibt sich entsprechend der Grafik zu | ||
Revision as of 20:50, 12 September 2022
Contents
Block error probability for RSC and BDD
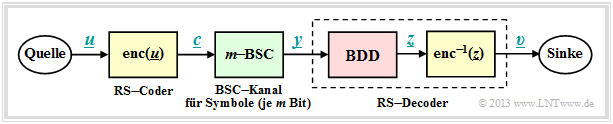
For error probability calculation we start from the same block diagram as in chapter "Error correction according to Reed-Solomon coding" , but here we choose the codeword estimator $(\underline {y} → \underline {z})$ to "Bounded Distance Decoding" $\rm (BDD)$ . For Maximum Likelihood Decoding the results are slightly better.
Let the block error probability be defined as follows:
- \[{ \rm Pr(Block\:error)} = { \rm Pr}( \underline{v} \ne \underline{u})= { \rm Pr}( \underline{z} \ne \underline{c}) = { \rm Pr}( f >t) \hspace{0.05cm}.\]
Due to the BDD assumption, the same simple result is obtained as for the binary block codes, namely the probability that the number $f$ of errors in the block (received word) is greater than the correctability $t$ of the code.
Since for the random variable $f$ (number of errors) there is a "Binomial distribution" in the range $0 ≤ f ≤ n$ we obtain:
- \[{\rm Pr(Block\:error)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.\]
But while in the first main chapter always $c_i ∈ \rm GF(2)$ has applied and thus the $f$ transmission errors were in each case bit errors, in Reed– Solomon coding under a transmission error $(y_i \ne c_i)$ because of $c_i ∈ {\rm GF}(2^m)$ and $y_i ∈ {\rm GF}(2^m)$ a symbol error.
This results in the following differences:
- The discrete channel model used to describe the binary block codes is the "Binary Symmetric Channel" (BSC). Each bit $c_i$ of a codeword is corrupted with probability $\varepsilon$ and correctly transmitted with probability $1-\varepsilon$ $(y_i = c_i)$.
- For Reed–Solomon–coding, one must replace the BSC model with the $m$ BSC channel model. A symbol $c_i$ is corrupted with probability $\varepsilon_{\rm S}$ into another symbol $y_i$ (no matter which one) and arrives with probability $1-\varepsilon_{\rm S}$ uncorrupted at the receiver.
$\text{Example 1:}$ We start from the BSC parameter $\varepsilon = 0.1$ and consider Reed–Solomon code symbols $c_i ∈ {\rm GF}(2^8)$ ⇒ $m = 8$, $q = 256$, $n = 255$.
For a symbol corruption $(y_i \ne c_i)$ already one wrong bit is sufficient. Or expressed differently: If $y_i = c_i$ is to be valid, then all $m = 8$ bits of the code symbol must be transmitted correctly:
- \[1 - \varepsilon_{\rm S} = (1 - \varepsilon)^m = 0.9^8 \approx 0.43 \hspace{0.05cm}.\]
- Thus, for the 8 BSC model, the falsification probability $\varepsilon_{\rm S} ≈ 0.57$.
- With the further assumption that the falsification of $c_i = \beta$ into any other symbol $y_i = \gamma \ne \beta$ is equally likely, we obtain:
- $${\rm Pr}(y_i = \gamma\hspace{0.05cm}\vert \hspace{0.05cm}c_i = \beta = 0.57/255 ≈ 0.223\%.$$
Application of Reed–Solomon coding for binary channels
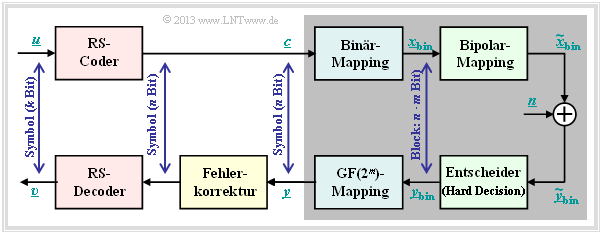
The prerequisites for the following calculation of the block error probability of a system with Reed–Solomon coding and conversion to binary symbols are summarized in the diagram:
- Assume a $(n, k)$ Reed–Solomon coding with symbols of $c_i ∈ {\rm GF}(2^m)$. The smaller the code rate $R=k/m$ is, the less information can be transmitted at a fixed data rate.
- Each symbol is represented by $m$ bits in binary ⇒ binary mapping. A block $($code word $\underline {c} )$ thus consists of $n$ symbols or of $n \cdot m$ binary characters (bits) combined in $\underline {c}_{\rm bin} $ .
- In addition, the "AWGN Channel", identified by the parameter $E_{\rm B}/N_0 $ is assumed. According to this channel model the transmission happens bipolar: "0" ↔ $+1$ and "1" ↔ $-1$.
- The receiver makes hard decisions on bit level. Before decoding including error correction, the binary symbols are converted back to ${\rm GF}(2^m)$ symbols.
The equation given on the last page (valid for Bounded Distance Decoding),
- \[{\rm Pr(Block\:error)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm},\]
is based on the $m$ BSC channel. Starting from the AWGN–channel (Additive White Gaussian Noise ), the "complementary Gaussian error integral" ${\rm Q}(x)$ to the BSC parameter
- \[\varepsilon = {\rm Q} \big (\sqrt{2 \cdot E_{\rm S}/N_0} \big ) = {\rm Q} \big (\sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \big ) \hspace{0.05cm},\]
comes from this to the symbol-level corruption probability $\varepsilon_{\rm S}$:
- \[\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m \hspace{0.05cm}.\]
$\text{Example 2:}$ One gets with
- $R=k/n = 239/255 = 0.9373$,
- $10 \cdot \lg \ E_{\rm B}/N_0 = 7 \, \rm dB$ ⇒ $E_{\rm B}/N_0 ≈ 5$, und
- $n = 2^8-1$ ⇒ $m = 8$
for the parameters $\varepsilon$ of the BSC model and $\varepsilon_{\rm S}$ of the 8 BSC model the following numerical values:
- $$\varepsilon = {\rm Q} \big (\sqrt{2 \cdot 0.9373 \cdot 5} \big ) = {\rm Q} \big (3.06\big ) \approx 1.1 \cdot 10^{-3}=0.11 \cdot \%$$
- $$\Rightarrow\hspace{0.3cm} \varepsilon_{\rm S} = 1 - (1 - 1.1 \cdot 10^{-3})^8 = 1 - 0.9989^8 = 1 - 0.9912 \approx 0.88 \cdot \% \hspace{0.2cm}(\approx 8 \cdot \varepsilon)\hspace{0.05cm}.$$
So every single symbol is transmitted with more than $99$ percent probability without errors.
BER of Reed–Solomon coding for binary channels
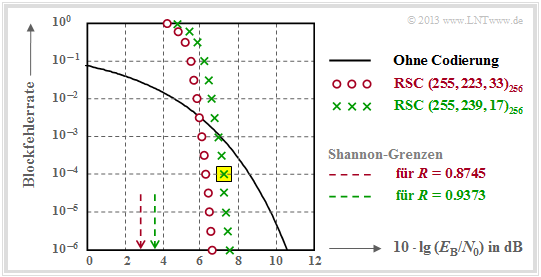
The following graph shows the block error probabilities given in [Liv10][1] given block error probabilities as a function of the AWGN quotient $10 \cdot \lg \ E_{\rm B}/N_0$.
Shown are the calculated curves ${ \rm Pr}( \underline{v} \ne \underline{u})$ for two different Reed–Solomon–codes corresponding to the Deep Space Standards according to CCSDS (Consultative Committee for Space Data Systems), namely
- the $\text{RSC (255, 239, 17)}_{256}$ with $R=0.9373$, which can correct up to $t = 8$ errors, and
- the $\text{RSC (255, 223, 33)}_{256}$ with higher correction capability $(t = 16)$ due to smaller code rate.
Hint: Die nachfolgend nur angedeutete Berechnung sollen Sie in der Aufgabe 2.15 für den $\text{RSC (7, 3, 5)}_{8}$ – also für etwas übersichtlichere Parameter – vollständig durchführen.
Wir analysieren den in der Grafik gelb hinterlegten Punkt, gültig für den $\text{RSC (255, 239, 17)}_{256}$ und $10 \cdot \lg \ E_{\rm B}/N_0 = 7.1 \,\rm dB$ ⇒ $\varepsilon = 0.007$. Die dazugehörige Blockfehlerwahrscheinlichkeit ergibt sich entsprechend der Grafik zu
- \[{\rm Pr(Blockfehler)} = \sum_{f =9}^{255} {255 \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{255-f}\approx 10^{-4} \hspace{0.05cm}.\]
Dominant ist hierbei der erste Term $($für $f=9)$, der bereits etwa $80\%$ ausmacht:
- \[{255 \choose 9} \approx 1.1 \cdot 10^{16}\hspace{0.05cm},\hspace{0.15cm} \varepsilon_{\rm S}^9 \approx 4 \cdot 10^{-20}\hspace{0.05cm},\hspace{0.15cm} (1 -\varepsilon_{\rm S})^{246} \approx 0.18 \hspace{0.15cm} \Rightarrow \hspace{0.15cm} {\rm Pr}(f = 9) \approx 8 \cdot 10^{-5} \hspace{0.05cm}.\]
Dies soll als Beleg dafür gelten, dass man die Summation schon nach wenigen Termen abbrechen darf.
Die in der Grafik dargestellten Ergebnisse kann man wie folgt zusammenfassen:
- Für kleines $E_{\rm B}/N_0$ (des AWGN–Kanals) sind die Reed–Solomon–Codes völlig ungeeignet. Beide Codes liegen für $10 \cdot \lg \ E_{\rm B}/N_0 < 6 \,\rm dB$ über der (schwarzen) Vergleichskurve für uncodierte Übertragung.
- Die Berechung für den $\text{RSC (255, 223, 33)}_{256}$ unterscheidet sich von obiger Rechnung nur in der unteren Summationsgrenze $(f_{\rm min} = 17)$ und durch ein etwas größeres $\varepsilon_{\rm S}$ $($wegen $R = 0.8745)$.
- Dieser "rote" Code $($mit $t = 16)$ ist für $\rm BER = 10^{-6}$ auch nur um etwa $1 \, \rm dB$ besser als der durch grüne Kreuze gekennzeichnete Code mit $t = 8$. Die Ergebnisse beider Codes sind also eher enttäuschend.
$\text{Fazit:}$
- Reed–Solomon–Codes sind beim gedächtnislosen Binärkanal (AWGN–Kanal) nicht sehr gut. Beide Codes liegen mehr als $4 \, \rm dB$ von der informationstheoretischen Shannon–Grenze entfernt.
- Reed–Solomon–Codes sind dagegen sehr wirkungsvoll bei so genannten Bündelfehlerkanälen. Sie werden deshalb vorwiegend bei Fadingkanälen, Speichersysteme, usw. eingesetzt.
- Die Reed–Solomon–Codes sind nicht perfekt. Welche Konsequenzen sich daraus ergeben, wird in der Aufgabe 2.16 behandelt.
Typische Anwendungen mit Reed–Solomon–Codierung
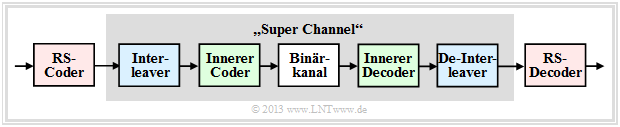
Reed–Solomon–Codierung wird häufig entsprechend der Grafik zusammen mit einem inneren Code in kaskadierter Form angewandt.
- Der innere Code ist fast immer ein Binärcode und in der Satelliten– und Mobilkommunikation oft ein Faltungscode.
- Will man nur die Reed–Solomon–Codierung/Decodierung untersuchen, so ersetzt man in einer Simulation die grau hinterlegten Komponenten durch einen einzigen Block, den man "Super Channel" nennt.
Besonders effizient ist ein solches verkettetes (englisch: concatenated) Codiersystem, wenn zwischen den beiden Codierern ein Interleaver geschaltet ist, um Bündelfehler weiter zu entspreizen.
$\text{Beispiel 3:}$ Die Grafik zeigt beispielhaft einen solchen Interleaver, wobei wir uns auf eine $20 × 4$–Matrix beschränken. In der Praxis sind diese Matrizen deutlich größer.
Der Interleaver wird zeilenweise beschrieben und spaltenweise ausgelesen (blaue Beschriftung). Beim De–Interleaver (grüne Beschriftung) ist die Reihenfolge genau umgekehrt.
- Die Reed–Solomon–Symbole werden also nicht fortlaufend an den inneren Coder weitergeleitet, sondern entsprechend der angegebenen Reihenfolge als Symbol 1, 21, 41, 61, 2, 22, usw. .
- Auf dem Kanal wird ein zusammenhängender Bereich (hier die Symbole 42, 62, 3, 23, 43, 63, 4, 24 ⇒ um das unten rot umrandete Rechteck) zerstört, zum Beispiel durch einen Kratzer auf dem Kanal "Speichermedium".
- Nach dem De–Interleaving ist die Symbolreihenfolge wieder 1, 2, 3, ... Man erkennt an den rot umrandeten Kreisen, dass nun dieses Fehlerbündel weitgehend "aufgebrochen" wurde.
$\text{Beispiel 4:}$ Eine sehr weit verbreitete Anwendung von Reed–Solomon–Codierung – und zudem die kommerziell erfolgreichste – ist die Compact Disc $\rm (CD)$, deren Fehlerkorrekturmechanismus bereits im Einführungkapitel dieses Buches beschrieben wurde. Hier ist der innere Code ebenfalls ein Reed–Solomon–Code, und das verkette Codiersystem lässt sich wie folgt beschreiben:
- Beide Kanäle des Stereo–Audiosignals werden mit je $\text{44.1 kHz}$ abgetastet und jeder einzelne Abtastwert wird mit $32$ Bit (vier Byte) digital dargestellt.
- Die Gruppierung von sechs Samples ergibt einen Rahmen $(192$ Bit$)$ und damit $24$ Codesymbole aus dem Galoisfeld $\rm GF(2^8)$. Jedes Codesymbol entspricht somit genau einem Byte.
- Der erste Reed–Solomon–Code mit der Rate $R_1 = 24/28$ liefert $28$ Byte, die einem Interleaver der Größe $28 × 109$ Byte zugeführt werden. Das Auslesen erfolgt (kompliziert) diagonal.
- Der Interleaver verteilt zusammenhängende Bytes großräumig über die gesamte Disk. Dadurch werden so genannte Bursts "aufgelöst", die zum Beispiel durch Kratzer auf der $\rm CD$ herrühren.
- Zusammen mit dem zweiten Reed–Solomon–Code $($Rate $R_2 = 28/32)$ ergibt sich eine Gesamtrate von $R = (24/28) · (28/32) = 3/4$. Beide Codes können jeweils $t = 2$ Symbolfehler korrigieren.
- Die beiden Komponentencodes $\text{RSC (28, 24, 5)}$ und $\text{RSC (32, 28, 5)}$ basieren jeweils auf dem Galoisfeld $\rm GF(2^8)$, was eigentlich die Codelänge $n = 255$ bedeuten würde.
- Die hier benötigten kürzeren Komponentencodes ergeben sich aus aus dem $\text{RSC (255, 251, 5)}_{256}$ durch Shortening ⇒ siehe Aufgabe 1.9Z. Durch diese Maßnahme wird aber die minimale Distanz $d_{\rm min}= 5$ nicht verändert.
- Mit der anschließenden Eight–to–Fourteen–Modulation und weiterer Kontrollsymbole kommt man schließlich zur endgültigen Coderate $ R = 192/588 ≈ 0.326$ der CD–Datenkomprimierung.
Auf der Seite Geschlitzte CD kann man sich anhand eines Audio–Beispiels von der Korrekturfähigkeit dieser cross–interleaved Reed–Solomon–Codierung überzeugen, aber auch deren Grenzen erkennen.
Aufgaben zum Kapitel
Aufgabe 2.15: RS-Blockfehlerwahrscheinlichkeit bei AWGN
Aufgabe 2.15Z: Nochmals RS-Blockfehlerwahrscheinlichkeit
Aufgabe 2.16: Entscheidungskriterien bei BDD
Quellenverzeichnis
- ↑ Liva, G.: Channel Coding. Lecture Notes, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2010.