Difference between revisions of "Channel Coding/Klassifizierung von Signalen"
| Line 94: | Line 94: | ||
*[[Komplementäre Gaußsche Fehlerfunktion Please add link and do not upload flash files.]]<br> | *[[Komplementäre Gaußsche Fehlerfunktion Please add link and do not upload flash files.]]<br> | ||
| + | == Binary Symmetric Error & Erasure Channel – BSEC == | ||
| + | <br> | ||
| + | Das BEC–Modell ist aufgrund der Fehlerwahrscheinlichkeit 0 eher unrealistisch und nur eine Näherung für ein extrem großes Signal–zu–Rausch–Leistungsverhältnis (kurz SNR) <i>ρ</i>. Stärkere Störungen ⇒ ein kleineres <i>ρ</i> sollten besser durch den <i>Binary Symmetric Error & Erasure Channel</i> (BSEC) mit den zwei Parametern | ||
| + | *Verfälschungswahrscheinlichkeit <i>ε</i> = Pr (<i>y</i> = 1 | <i>x</i> = 0) = Pr (<i>y</i> = 0 | <i>x</i> = 1),<br> | ||
| + | *Erasure–Wahrscheinlichkeit <i>λ</i> = Pr(<i>y</i> = E | <i>x</i> = 0) = Pr(<i>y</i> = E | <i>x</i> = 1)<br><br> | ||
| + | modelliert werden. Es gilt auch hier <i>x</i> ∈ {0, 1} und <i>y</i> ∈ {0, 1, E}.<br> | ||
| + | [[File:P ID2344 KC T 1 2 S4 v2.png|Binary Error & Erasure Channel (BEEC) und Zusammenhang mit dem AWGN–Modell|class=fit]]<br> | ||
| + | {{Beispiel}}''':''' Wir betrachten das BSEC–Modell mit den beiden Entscheidungsgeraden <i>G</i><sub>0</sub> = <i>G</i> = 0.5 und <i>G</i><sub>1</sub> = –<i>G</i>, dessen Parameter <i>ε</i> und <i>λ</i> durch das SNR <i>ρ</i> = 1/<i>σ</i><sup>2</sup> des vergleichbaren AWGN–Kanals festgelegt sind. Dann gilt | ||
| + | *für <i>σ</i> = 0.5 ⇒ <i>ρ</i> = 4: | ||
| + | ::<math>\varepsilon \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Q}[\sqrt{\rho} \cdot (1 + G)] = {\rm Q}(3) \approx 0.14\%\hspace{0.05cm},</math> | ||
| + | ::<math>{\it \lambda} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Q}[\sqrt{\rho} \cdot (1 - G)] - \varepsilon = {\rm Q}(1) - {\rm Q}(3) \approx 15.87\% - 0.14\% = 15.73\%\hspace{0.05cm},</math> | ||
| + | *für <i>σ</i> = 0.25 ⇒ <i>ρ</i> = 16: | ||
| + | ::<math>\varepsilon = {\rm Q}(6) \approx 10^{-10}\hspace{0.05cm},\hspace{0.2cm} | ||
| + | {\it \lambda} = {\rm Q}(2) \approx 2.27\%\hspace{0.05cm}.</math> | ||
| + | Für die rechts dargestellte WDF wurde <i>ρ</i> = 4 vorausgesetzt. Für <i>ρ</i> = 16 könnte das BSEC–Modell durch die BEC–Variante ersetzt werden, ohne dass es zu einer gravierenden Verfälschung kommt.{{end}}<br> | ||
Revision as of 21:14, 8 January 2017
Contents
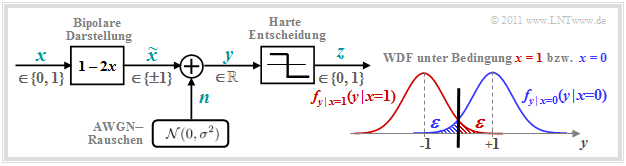
AWGN–Kanal bei binärem Eingang
Wir betrachten das bekannte zeitdiskrete AWGN–Kanalmodell gemäß der unteren Grafik (links):
- Das binäre und zeitdiskrete Nachrichtensignal x nimmt mit gleicher Wahrscheinlichkeit die Werte 0 und 1 an, das heißt, es ist Pr(x = 0) = Pr(x̃ = +1) = 1/2 sowie Pr(x = 1) = Pr(x̃ = –1) = 1/2.
- Die Übertragung wird durch additives weißes gaußverteiltes Rauschen (AWGN) n mit der (normierten) Rauschleistung σ2 = N0/(2ES) beeinträchtigt. Die Streuung der Gauß–WDF ist σ.
- Aufgrund der Gaußschen WDF kann das Ausgangssignal y = x̃ + n alle reellen Werte annehmen. Der Signalwert y ist zwar wie x̃ zeitdiskret, im Gegensatz zu diesem aber wertkontinuierlich.
Die rechte Grafik zeigt die bedingten Wahrscheinlichkeitsdichtefunktionen (in blau bzw. rot):
\[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=0 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=0 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot \exp \left [ - \frac {(y-1)^2}{2\sigma^2} \right ]\hspace{0.05cm},\] \[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot \exp \left [ - \frac {(y+1)^2}{2\sigma^2} \right ]\hspace{0.05cm}.\]
Nicht dargestellt ist die gesamte (unbedingte) WDF, für die bei gleichwahrscheinlichen Symbolen gilt:
\[f_y(y) = {1}/{2} \cdot \left [ f_{y \hspace{0.03cm}| \hspace{0.03cm}x=0 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=0 ) + f_{y \hspace{0.03cm}| \hspace{0.03cm}x=1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=1 )\right ]\hspace{0.05cm}.\]
Die beiden schraffierten Flächen (jeweils ε) markieren Entscheidungsfehler unter der Voraussetzung <nobr>x = 0</nobr> ⇒ x̃ = +1 (blau) bzw. x = 1 ⇒ x̃ = –1 (rot), wenn harte Entscheidungen getroffen werden:
\[z = \left\{ \begin{array}{c} 0\\ 1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls} \hspace{0.15cm} y > 0\hspace{0.05cm},\\ {\rm falls} \hspace{0.15cm}y < 0\hspace{0.05cm}.\\ \end{array}\]
Bei gleichwahrscheinlichen Eingangssymbolen ist dann die mittlere Bitfehlerwahrscheinlichkeit Pr(z ≠ x) ebenfalls gleich ε. Mit dem Komplementären Gaußschen Fehlerintergral Please add link and do not upload flash videos. Q(x) gilt dabei:
\[\varepsilon = {\rm Q}(1/\sigma) = {\rm Q}(\sqrt{\rho}) = \frac {1}{\sqrt{2\pi} } \cdot \int_{\sqrt{\rho}}^{\infty}{\rm e}^{- \alpha^2/2} \hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.\]
Hierbei bezeichnet ρ = 1/σ2 = 2 · ES/N0 das Signal–zu–Rauschverhältnis (SNR) vor dem Entscheider, wobei folgende Systemgrößen verwendet werden:
- ES ist die Signalenergie pro Symbol (ohne Codierung gleich EB, also der Signalenergie pro Bit),
- N0 bezeichnet die konstante (einseitige) Rauschleistungsdichte des AWGN–Kanals.
Wir verweisen hier auf das interaktive Flash–Modul Fehlerwahrscheinlichkeit von Digitalsystemen Please add link and do not upload flash videos.
Binary Symmetric Channel – BSC
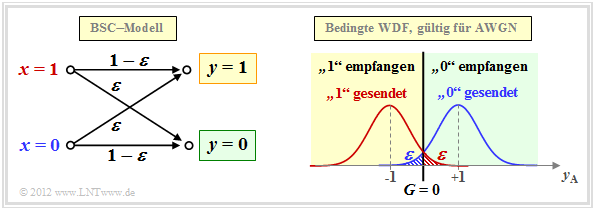
Das AWGN–Kanalmodell ist kein digitales Kanalmodell, wie wir es im Kapitel 1.1 zur Beschreibung der Kanalcodierverfahren vorausgesetzt haben. Berücksichtigen wir aber eine harte Entscheidung, so kommen wir zum digitalen Modell Binary Symmetric Channel (BSC):
Wählt man die Verfälschungswahrscheinlichkeiten Pr(y = 1 | x = 0) bzw. Pr(y = 0 | x = 1) jeweils zu
\[\varepsilon = {\rm Q}(\sqrt{\rho})\hspace{0.05cm},\]
so ist der Zusammenhang zum AWGN–Kanalmodell hergestellt. Die Entscheidungsgrenze liegt dabei bei G = 0, wodurch auch die Eigenschaft „symmetrisch” begründet ist.
Hinweis: Beim AWGN–Modell haben wir die binäre Ausgangsgröße (nach Schwellenwertentscheidung) mit z ∈ {0, 1} bezeichnet. Bei den digitalen Kanalmodellen (BSC, BEC, BSEC) bezeichnen wir nun den wertdiskreten Ausgang wieder mit y. Um Verwechslungen zu vermeiden, nennen wir das Ausgangssignal des AWGN –Modells nun yA. Für das analoge Empfangssignal gilt yA = x̃ + n.
Das BSC–Modell liefert eine statistisch unabhängige Fehlerfolge und eignet sich somit zur Modellierung gedächtnisloser rückkopplungsfreier Kanäle, die in diesem Buch ausnahmslos betrachtet werden.
Zur Beschreibung gedächtnisbehafteter Kanäle müssen andere Modelle herangezogen werden, die im Kapitel 5 des Buches „Digitalsignalübertragung” behandelt werden, zum Beispiel Bündelfehler nach
- dem Gilbert–Elliott–Modell,
- dem McCullough–Kanalmodell.
Die Abbildung zeigt statistisch unabhängige Fehler nach dem BSC–Modell (links) und so genannte Bündelfehler gemäß Gilbert–Elliott (rechts), wobei die Bitfehlerrate in beiden Fällen 10% beträgt. Aus der rechten Grafik ist zu erkennen, dass das Bild zeilenweise übertragen wird.
Binary Erasure Channel – BEC
Das BSC–Modell liefert nur die Aussagen „richtig” und „falsch”. Manche Empfänger – so zum Beispiel die so genannten Soft–in Soft–out Decoder – können jedoch auch gewisse Informationen über die Sicherheit der Entscheidung liefern, wobei sie natürlich darüber informiert werden müssen, welche ihrer Eingangswerte sicher sind und welche eher unsicher.
Der Binary Erasure Channel (BEC) liefert eine solche Information. Anhand der Grafik erkennt man:
- Das Eingangsalphabet des BEC–Kanalmodells ist binär ⇒ x ∈ {0, 1} und das Ausgangsalphabet ternär ⇒ y ∈ {0, 1, E}. Ein „E” kennzeichnet eine unsichere Entscheidung. Dieses neue „Symbol” steht für Erasure, zu deutsch: Auslöschung.
- Bitfehler werden durch das BEC–Modell per se ausgeschlossen. Eine unsichere Entscheidung (E) wird mit der Wahrscheinlichkeit λ getroffen, während die Wahrscheinlichkeit für eine richtige (und gleichzeitig sichere) Entscheidung 1 – λ beträgt.
- Rechts oben ist der Zusammenhang zwischen BEC– und AWGN–Kanalmodell dargestellt, wobei das Erasure–Entscheidungsgebiet („E”) grau hinterlegt ist. Man erkennt, dass es im Gegensatz zum BSC–Modell (G = 0) nun zwei Entscheidungsgrenzen G0 = G und G1 = –G gibt, und es gilt:
- \[\lambda = {\rm Q}[\sqrt{\rho} \cdot (1 - G)]\hspace{0.05cm}.\]
Wir weisen hier nochmals auf zwei interaktive Flash–Module hin:
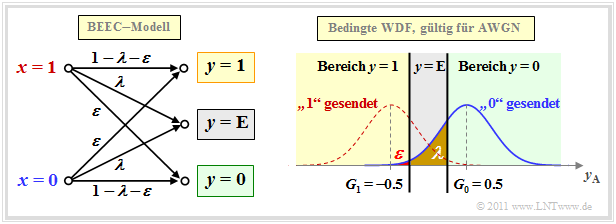
Binary Symmetric Error & Erasure Channel – BSEC
Das BEC–Modell ist aufgrund der Fehlerwahrscheinlichkeit 0 eher unrealistisch und nur eine Näherung für ein extrem großes Signal–zu–Rausch–Leistungsverhältnis (kurz SNR) ρ. Stärkere Störungen ⇒ ein kleineres ρ sollten besser durch den Binary Symmetric Error & Erasure Channel (BSEC) mit den zwei Parametern
- Verfälschungswahrscheinlichkeit ε = Pr (y = 1 | x = 0) = Pr (y = 0 | x = 1),
- Erasure–Wahrscheinlichkeit λ = Pr(y = E | x = 0) = Pr(y = E | x = 1)
modelliert werden. Es gilt auch hier x ∈ {0, 1} und y ∈ {0, 1, E}.
- für σ = 0.5 ⇒ ρ = 4:
- \[\varepsilon \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Q}[\sqrt{\rho} \cdot (1 + G)] = {\rm Q}(3) \approx 0.14\%\hspace{0.05cm},\]
- \[{\it \lambda} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Q}[\sqrt{\rho} \cdot (1 - G)] - \varepsilon = {\rm Q}(1) - {\rm Q}(3) \approx 15.87\% - 0.14\% = 15.73\%\hspace{0.05cm},\]
- für σ = 0.25 ⇒ ρ = 16:
- \[\varepsilon = {\rm Q}(6) \approx 10^{-10}\hspace{0.05cm},\hspace{0.2cm} {\it \lambda} = {\rm Q}(2) \approx 2.27\%\hspace{0.05cm}.\]