Difference between revisions of "Channel Coding/The Basics of Low-Density Parity Check Codes"
| (40 intermediate revisions by 3 users not shown) | |||
| Line 8: | Line 8: | ||
== Some characteristics of LDPC codes == | == Some characteristics of LDPC codes == | ||
<br> | <br> | ||
| − | The | + | The "Low–density Parity–check Codes" $($in short: »'''LDPC codes'''«$)$ were invented as early as the early 1960s and date back to the dissertation [Gal63]<ref name ='Gal63'>Gallager, R. G.: Low-density parity-check codes. MIT Press, Cambridge, MA, 1963.</ref> by [https://en.wikipedia.org/wiki/Robert_G._Gallager $\text{Robert G. Gallager}$].<br> |
| − | However, the idea came several decades too early due to the processor technology of the time. Only three years after Berrou's invention of the turbo codes in 1993, however, [https://en.wikipedia.org/wiki/David_J._C._MacKay David J. C. MacKay] and [https://en.wikipedia.org/wiki/Radford_M._Neal | + | However, the idea came several decades too early due to the processor technology of the time. Only three years after Berrou's invention of the turbo codes in 1993, however, [https://en.wikipedia.org/wiki/David_J._C._MacKay $\text{David J. C. MacKay}$] and [https://en.wikipedia.org/wiki/Radford_M._Neal $\text{Radford M. Neal}$] recognized the huge potential of the LDPC codes if they were decoded iteratively symbol by symbol just like the turbo codes. They virtually reinvented the LDPC codes.<br> |
| − | As can already be seen from the name component "parity–check" | + | As can already be seen from the name component "parity–check" that these codes are linear block codes according to the explanations in the [[Channel_Coding/Objective_of_Channel_Coding#.23_OVERVIEW_OF_THE_FIRST_MAIN_CHAPTER_.23|"first main chapter" ]]. Therefore, the same applies here: |
| − | *The code word results from the information word $\underline{u}$ (represented with $k$ binary symbols) and the [[Channel_Coding/General_Description_of_Linear_Block_Codes#Code_definition_by_the_generator_matrix| | + | *The code word results from the information word $\underline{u}$ $($represented with $k$ binary symbols$)$ and the [[Channel_Coding/General_Description_of_Linear_Block_Codes#Code_definition_by_the_generator_matrix|$\text{generator matrix}$]] $\mathbf{G}$ of dimension $k × n$ to $\underline{x} = \underline{u} \cdot \mathbf{G}$ ⇒ code word length $n$.<br> |
| − | *The parity-check equations result from the identity $\underline{x} \cdot \mathbf{H}^{\rm T} ≡ 0$, where $\mathbf{H}$ denotes the parity-check matrix. This consists of $m$ rows and $n$ columns. While in the first chapter basically $m = n -k$ was valid, for the LPDC codes we only require $m ≥ n -k$. | + | *The parity-check equations result from the identity $\underline{x} \cdot \mathbf{H}^{\rm T} ≡ 0$, where $\mathbf{H}$ denotes the parity-check matrix. This consists of $m$ rows and $n$ columns. While in the first chapter basically $m = n -k$ was valid, for the LPDC codes we only require $m ≥ n -k$.<br> |
| − | A serious difference between an LDPC code and a conventional block code as described in the first chapter is that the parity-check matrix $\mathbf{H}$ is sparsely populated with ones | + | *A serious difference between an LDPC code and a conventional block code as described in the first main chapter is that the parity-check matrix $\mathbf{H}$ is here sparsely populated with "ones" ⇒ "low-density".<br> |
| − | |||
| − | |||
| − | |||
| − | *the LDPC code from [Liv15]<ref name='Liv15'>Liva, G.: | + | {{GraueBox|TEXT= |
| + | [[File:EN_KC_T_4_4_S1a_v3.png|right|frame|Parity-check matrices of a Hamming code and a LDPC code|class=fit]] | ||
| + | $\text{Example 1:}$ The graph shows parity-check matrices $\mathbf{H}$ for | ||
| + | |||
| + | *the Hamming code with code length $n = 15$ and with $m = 4$ parity-check equations ⇒ $k = 11$ information bits,<br> | ||
| + | |||
| + | *the LDPC code from [Liv15]<ref name='Liv15'>Liva, G.: Channels Codes for Iterative Decoding. Lecture notes, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2015.</ref> of length $n = 12$ and with $m = 9$ parity-check equations ⇒ $k ≥ 3$ information bits.<br><br> | ||
| − | + | <u>Remarks:</u> | |
| + | #In the left graph, the proportion of "ones" is $32/60 \approx 53.3\%$. | ||
| + | #In the right graph the share of "ones" is lower with $36/108 = 33.3\%$. | ||
| + | #For LDPC codes $($relevant for practice ⇒ with long length$)$, the share of "ones" is even significantly lower.<br> | ||
| − | |||
| − | |||
We now analyze the two parity-check matrices using the rate and Hamming weight:<br> | We now analyze the two parity-check matrices using the rate and Hamming weight:<br> | ||
| − | *The rate of the Hamming code under consideration (left graph) is $R = k/n = 11/15 \approx 0.733$. The Hamming weight of each of the four rows is $w_{\rm | + | *The rate of the Hamming code under consideration $($left graph$)$ is $R = k/n = 11/15 \approx 0.733$. The Hamming weight of each of the four rows is $w_{\rm R}= 8$, while the Hamming weights $w_{\rm C}(i)$ of the columns vary between $1$ and $4$. For the columns index variable here: $1 ≤ i ≤ 15$. |
| − | *In the considered LDPC | + | *In the considered LDPC code there are four "ones" in all rows ⇒ $w_{\rm R} = 4$ and three "ones" in all columns ⇒ $w_{\rm C} = 3$. The code label $(w_{\rm R}, \ w_{\rm C})$ of LDPC code uses exactly these parameters. Note the different nomenclature to the "$(n, \ k, \ m)$ Hamming code". |
| − | |||
| − | |||
| + | *This is called a »<b>regular LDPC code</b>«, since all row weights $w_{\rm R}(j)$ for $1 ≤ j ≤ m$ are constant equal $w_{\rm R}$ and also all column weights $($with indices $1 ≤ i ≤ n)$ are equal: $w_{\rm C}(i) = w_{\rm C} = {\rm const.}$ If this condition is not met, there is an "irregular LDPC code".}}<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Feature of LDPC codes}$ | $\text{Feature of LDPC codes}$ | ||
| − | For the code rate, one can generally (if $k$ is not known) specify only | + | *For the code rate, one can generally $($if $k$ is not known$)$ specify only a bound: |
| − | :$$R ≥ 1 - w_{\rm | + | :$$R ≥ 1 - w_{\rm C}/w_{\rm R}.$$ |
| − | *The equal sign holds if all rows of $\mathbf{H}$ are linearly independent ⇒ $m = n \, – k$. Then the conventional equation is obtained: | + | *The equal sign holds if all rows of $\mathbf{H}$ are linearly independent ⇒ $m = n \, – k$. Then the conventional equation is obtained: |
| − | :$$R = 1 - w_{\rm | + | :$$R = 1 - w_{\rm C}/w_{\rm R} = 1 - m/n = k/n.$$ |
| − | *In contrast, for the code rate of an irregular LDPC code and also for the $(15, 11, 4)$ Hamming code sketched on the left: | + | *In contrast, for the code rate of an irregular LDPC code and also for the $(15, 11, 4)$ Hamming code sketched on the left: |
| − | :$$R \ge 1 - \frac{ {\rm E}[w_{\rm | + | :$$R \ge 1 - \frac{ {\rm E}[w_{\rm C}]}{ {\rm E}[w_{\rm R}]} |
| − | \hspace{0.5cm}{\rm | + | \hspace{0.5cm}{\rm with}\hspace{0.5cm} |
| − | {\rm E}[w_{\rm | + | {\rm E}[w_{\rm C}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm C}(i) |
| − | \hspace{0.5cm}{\rm | + | \hspace{0.5cm}{\rm and}\hspace{0.5cm} |
| − | {\rm E}[w_{\rm | + | {\rm E}[w_{\rm R}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm R}(j) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *In Hamming codes the $m = n - k$ parity-check equations are linearly independent, the "$≥$" sign can be replaced by the "$=$" sign, which simultaneously means: | |
| + | :$$R = k/n.$$}}<br> | ||
| − | For more information on this topic, see [[Aufgaben:Exercise_4.11:_Analysis_of_Parity-check_Matrices| "Exercise 4.11"]] and [[Aufgaben:Exercise_4.11Z:_Code_Rate_from_the_Parity-check_Matrix| " Exercise 4.11Z"]]. | + | For more information on this topic, see [[Aufgaben:Exercise_4.11:_Analysis_of_Parity-check_Matrices| "Exercise 4.11"]] and [[Aufgaben:Exercise_4.11Z:_Code_Rate_from_the_Parity-check_Matrix| "Exercise 4.11Z"]]. |
== Two-part LDPC graph representation - Tanner graph == | == Two-part LDPC graph representation - Tanner graph == | ||
<br> | <br> | ||
| − | All essential features of a LDPC ode are contained in the parity-check matrix $\mathbf{H} = (h_{j,\hspace{0.05cm}i})$ and can be represented by a so-called | + | All essential features of a LDPC ode are contained in the parity-check matrix $\mathbf{H} = (h_{j,\hspace{0.05cm}i})$ and can be represented by a so-called "Tanner graph". It is a "bipartite graph representation". Before we examine and analyze exemplary Tanner graphs more exactly, first still some suitable description variables must be defined: |
| − | *The $n$ columns of the parity-check matrix $\mathbf{H}$ each represent one code word | + | *The $n$ columns of the parity-check matrix $\mathbf{H}$ each represent one bit of a code word. Since each code word bit can be both an information bit and a parity bit, the neutral name »<b>variable node </b>« $\rm (VN)$ has become accepted for this. The $i$<sup>th</sup> code word bit is called $V_i$ and the set of all variable nodes is $\{V_1, \text{...}\hspace{0.05cm} , \ V_i, \ \text{...}\hspace{0.05cm} , \ V_n\}$.<br> |
| − | *The $m$ rows of $\mathbf{H}$ each describe a parity-check equation. We refer to such a parity-check equation as <b>check node</b> (CN) | + | *The $m$ rows of $\mathbf{H}$ each describe a parity-check equation. We refer to such a parity-check equation in the following as »<b>check node</b>« $\rm (CN)$. The set of all check nodes is $\{C_1, \ \text{...}\hspace{0.05cm} , \ C_j, \ \text{...}\hspace{0.05cm} , \ C_m\}$, where $C_j$ denotes the parity-check equation of the $j$<sup>th</sup> row.<br> |
| − | *In the Tanner | + | *In the Tanner graph, the $n$ variable nodes $V_i$ are represented as circles and the $m$ check nodes $C_j$ as squares. If the $\mathbf{H}$ matrix element in row $j$ and column $i$ is $h_{j,\hspace{0.05cm}i} = 1$, there is an edge between the variable node $V_i$ and the check node $C_j$.<br><br> |
| − | [[File:P ID3069 KC T 4 4 S2a v3.png|right|frame| | + | {{GraueBox|TEXT= |
| − | + | [[File:P ID3069 KC T 4 4 S2a v3.png|right|frame|Example of a Tanner graph|class=fit]] | |
| − | $\text{Example 2:}$ To clarify the above terms, an | + | $\text{Example 2:}$ To clarify the above terms, an exemplary Tanner graph is given on the right with |
| − | *the | + | *the variable nodes $V_1$ to $V_4$, and<br> |
| − | *the | + | |
| + | *the check nodes $C_1$ to $C_3$.<br><br> | ||
| − | However, the associated code has no practical meaning. | + | However, the associated code has no practical meaning. |
One can see from the graph: | One can see from the graph: | ||
| − | + | #The code length is $n = 4$ and there are $m = 3$ parity-check equations. | |
| − | + | #Thus the parity-check matrix $\mathbf{H}$ has dimension $3×4$.<br> | |
| − | + | #There are six edges in total. Thus six of the twelve elements $h_{j,\hspace{0.05cm}i}$ of matrix $\mathbf{H}$ are "ones".<br> | |
| + | #At each check node two lines arrive ⇒ the Hamming weights of all rows are equal: $w_{\rm R}(j) = 2 = w_{\rm R}$.<br> | ||
| + | #From the nodes $V_1$ and $V_4$ there is only one transition to a check node each, from $V_2$ and $V_3$, however, there are two. | ||
| + | #For this reason, it is an "irregular code".<br><br> | ||
| − | + | Accordingly, the parity-check matrix is: | |
| − | |||
| − | |||
| − | |||
| − | |||
::<math>{ \boldsymbol{\rm H} } = | ::<math>{ \boldsymbol{\rm H} } = | ||
| Line 94: | Line 98: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Example 3:}$ | + | $\text{Example 3:}$ Now a more practical example follows. In [[Aufgaben:Exercise_4.11:_Analysis_of_Parity-check_Matrices|"Exercise 4.11"]] two parity-check matrices were analyzed: |
| − | + | [[File:EN_KC_T_4_4_S2b_v1.png|right|frame|Tanner graph of a regular and an irregular code|class=fit]] | |
| − | + | ⇒ The encoder corresponding to the matrix $\mathbf{H}_1$ is systematic. | |
| + | #The code parameters are $n = 8, \ k = 4,\ m = 4$ ⇒ rate $R=1/2$. | ||
| + | #The code is irregular because the Hamming weights are not the same for all columns. | ||
| + | #In the graph, this "irregular $\mathbf{H}$ matrix" is given above.<br> | ||
| − | + | ⇒ Bottom indicated is the "regular $\mathbf{H}$ matrix" corresponding to the matrix $\mathbf{H}_3$ from Exercise 4.11. | |
| − | + | #The rows are linear combinations of the upper matrix $\mathbf{H}_1$. | |
| − | + | #For this non-systematic encoder holds $w_{\rm C} = 2, \ w_{\rm R} = 4$. | |
| − | *The left graph refers to the upper (irregular) matrix. The eight | + | #Thus for the rate: $R \ge 1 - w_{\rm C}/w_{\rm R} = 1/2$. |
| + | <br clear=all> | ||
| + | On the right you see the corresponding Tanner graphs: | ||
| + | *The left Tanner graph refers to the upper $($irregular$)$ matrix. The eight variable nodes $V_i$ are connected to the four check nodes $C_j$ if the element in row $j$ and column $i$ is a "one" $\hspace{0.15cm} ⇒ \hspace{0.15cm} h_{j,\hspace{0.05cm}i}=1$.<br> | ||
| − | *This graph is not particularly well suited for [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes# | + | *This graph is not particularly well suited for [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Iterative_decoding_of_LDPC_codes| $\text{iterative symbol-wise decoding}$]]. The variable nodes $V_5, \ \text{...}\hspace{0.05cm} , \ V_8$ are each associated with only one check node, which provides no information for decoding.<br> |
| − | *In the right Tanner | + | *In the right Tanner graph for the regular code, you can see that here from each variable node $V_i$ two edges come off and from each check node $C_j$ their four. This allows information to be gained during decoding in each iteration loop.<br> |
| − | *It can also be seen that here, in the transition from the irregular to the equivalent regular code, the ones& | + | *It can also be seen that here, in the transition from the irregular to the equivalent regular code, the proportion of "ones" increases, in the example from $37.5\%$ to $50\%$. However, this statement cannot be generalized.}}<br> |
== Iterative decoding of LDPC codes == | == Iterative decoding of LDPC codes == | ||
<br> | <br> | ||
| − | + | As an example of iterative LDPC decoding, the so-called "message passing algorithm" is now described. We illustrate this using the right-hand Tanner graph in [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Two-part_LDPC_graph_representation_-_Tanner_graph|$\text{Example 3}$]] in the previous section and thus for the regular parity-check matrix given there.<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Principle:}$ In the »<b>message passing algorithm</b>« there is an alternating $($or iterative$)$ exchange of information between the variable nodes $V_1, \ \text{...}\hspace{0.05cm} , \ V_n$ and the check nodes $C_1 , \ \text{...}\hspace{0.05cm} , \ C_m$.}}<br> |
| − | [[File: | + | [[File:EN_KC_T_4_4_S3a_v1.png|right|frame|Iterative decoding of LDPC codes|class=fit]] |
| − | + | For the regular LDPC code under consideration: | |
| − | + | #There are $n = 8$ variable nodes and $m = 4$ check nodes. | |
| + | # From each variable node go $d_{\rm V} = 2$ connecting lines to a check node and each check node is connected to $d_{\rm C} = 4$ variable nodes. | ||
| + | #The variable node degree $d_{\rm V}$ is equal to the Hamming weight of each column $(w_{\rm C})$ and for the check node degree holds: $d_{\rm C} = w_{\rm R}$ (Hamming weight of each row). | ||
| + | #In the following description we use the terms "neighbors of a variable node" ⇒ $N(V_i)$ and "neighbors of a check node" ⇒ $N(C_j)$. | ||
| + | #We restrict ourselves here to implicit definitions: | ||
| − | + | ::$$N(V_1) = \{ C_1, C_2\}\hspace{0.05cm},$$ | |
| + | ::$$ N(V_2) = \{ C_3, C_4\},$$ | ||
| + | :::::$$\text{........}$$ | ||
| + | ::$$N(V_8) = \{ C_1, C_4\},$$ | ||
| + | ::$$N(C_1) = \{ V_1, V_4, V_5, V_8\},$$ | ||
| + | :::::$$\text{........}$$ | ||
| + | ::$$N(C_4) = \{ V_2, V_3, V_6, V_8\}.$$ | ||
| − | + | {{GraueBox|TEXT= | |
| + | [[File:P ID3085 KC T 4 4 S3c v2.png|right|frame|Information exchange between variable and check nodes]] | ||
| + | $\text{Example 4:}$The sketch from [Liv15]<ref name='Liv15'>Liva, G.: Channels Codes for Iterative Decoding. Lecture notes, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2015.</ref> shows the information exchange | ||
| + | *between the yariable node $V_i$ and the check node $C_j$, | ||
| − | + | *expressed by [[Channel_Coding/Soft-in_Soft-Out_Decoder#Reliability_information_-_Log_likelihood_ratio| $\text{log likelihood ratios}$]] $(L$ values for short$)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The exchange of information happens in two directions: | |
| − | * | + | *$L(V_i → C_j)$: Extrinsic information from $V_i$ point of view, a-priori information from $C_j$ point of view.<br> |
| − | *<b>$L(C_j → V_i)$</b>: | + | *<b>$L(C_j → V_i)$</b>: Extrinsic information from $C_j$ point of view, a-priori information from $V_i$ point of view.}} |
| − | + | The description of the decoding algorithm continues:<br> | |
| − | <b> | + | <b>(1) Initialization:</b> At the beginning of decoding, the variable nodes receive no a-priori information from the check nodes, and it applies for $1 ≤ i ≤ n \text{:}$ |
:$$L(V_i → C_j) = L_{\rm K}(V_i).$$ | :$$L(V_i → C_j) = L_{\rm K}(V_i).$$ | ||
| − | + | As can be seen from the graph at the top of the page, these channel log likelihood values $L_{\rm K}(V_i)$ result from the received values $y_i$.<br><br> | |
| − | <b>Check Node Decoder</b>: | + | <b>(2) Check Node Decoder (CND)</b>: Each node $C_j$ represents one parity-check equation. Thus $C_1$ represents the equation $V_1 + V_4 + V_5 + V_8 = 0$. One can see the connection to extrinsic information in the symbol-wise decoding of the single parity–check code. |
| − | In | + | In analogy to the section [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios|"Calculation of extrinsic log likelihood ratios"]] and to [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC|"Exercise 4.4"]] thus applies to the extrinsic log likelihood value of $C_j$ and at the same time to the a-priori information concerning $V_i$: |
::<math>L(C_j \rightarrow V_i) = 2 \cdot {\rm tanh}^{-1}\left [ \prod\limits_{V \in N(C_j)\hspace{0.05cm},\hspace{0.1cm} V \ne V_i} \hspace{-0.35cm}{\rm tanh}\left [L(V \rightarrow C_j \right ] /2) \right ] | ::<math>L(C_j \rightarrow V_i) = 2 \cdot {\rm tanh}^{-1}\left [ \prod\limits_{V \in N(C_j)\hspace{0.05cm},\hspace{0.1cm} V \ne V_i} \hspace{-0.35cm}{\rm tanh}\left [L(V \rightarrow C_j \right ] /2) \right ] | ||
| Line 155: | Line 174: | ||
| − | <b>Variable Node Decoder</b>: | + | <b>(3) Variable Node Decoder (VND)</b>: In contrast to the check node decoder, the variable node decoder is related to the decoding of a repetition code because all check nodes connected to $V_i$ correspond to the same bit $C_j$ ⇒ this bit is quasi repeated $d_{\rm V}$ times.<br> |
| − | In | + | In analogy to to the section [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios| "Calculation of extrinsic log likelihood ratios"]] applies to the extrinsic log likelihood value of $V_i$ and at same time to the a-priori information concerning $C_j$: |
| + | [[File:EN_KC_T_4_4_S3b_v4.png|right|frame|Relationship between LDPC decoding and serial turbo decoding |class=fit]] | ||
::<math>L(V_i \rightarrow C_j) = L_{\rm K}(V_i) + \hspace{-0.55cm} \sum\limits_{C \hspace{0.05cm}\in\hspace{0.05cm} N(V_i)\hspace{0.05cm},\hspace{0.1cm} C \hspace{0.05cm}\ne\hspace{0.05cm} C_j} \hspace{-0.55cm}L(C \rightarrow V_i) | ::<math>L(V_i \rightarrow C_j) = L_{\rm K}(V_i) + \hspace{-0.55cm} \sum\limits_{C \hspace{0.05cm}\in\hspace{0.05cm} N(V_i)\hspace{0.05cm},\hspace{0.1cm} C \hspace{0.05cm}\ne\hspace{0.05cm} C_j} \hspace{-0.55cm}L(C \rightarrow V_i) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | The chart on the right describes the decoding algorithm for LDPC codes. | |
| + | *It shows similarities with the decoding method for [[Channel_Coding/The_Basics_of_Turbo_Codes#Serial_concatenated_turbo_codes_.E2.80.93_SCCC| $\text{serial concatenated turbo codes}$]]. | ||
| − | + | *To establish a complete analogy between LDPC and turbo decoding, an "interleaver" as well as a "de-interleaver" are also drawn here between $\rm VND$ and $\rm CND$. | |
| − | * | + | *Since these are not real system components, but only analogies, we have enclosed these terms in quotation marks.<br> |
| − | + | <br clear=all> | |
| + | == Performance of regular LDPC codes == | ||
| + | <br> | ||
| + | We now consider as in [Str14]<ref name='Str14'>Strutz, T.: Low-density parity-check codes - An introduction. Lecture material. Hochschule für Telekommunikation, Leipzig, 2014. PDF document.</ref> five regular LDPC codes. The graph shows the bit error rate $\rm (BER)$ depending on the AWGN parameter $10 \cdot {\rm lg} \, E_{\rm B}/N_0$. The curve for uncoded transmission is also plotted for comparison.<br> | ||
| + | [[File:EN_KC_T_4_4_S4a_v2.png|right|frame|Bit error rate of LDPC codes]] | ||
| + | These LDPC codes exhibit the following properties: | ||
| + | *The parity-check matrices $\mathbf{H}$ each have $n$ columns and $m = n/2$ linearly independent rows. In each row there are $w_{\rm R} = 6$ "ones" and in each column $w_{\rm C} = 3$ "ones".<br> | ||
| − | + | *The share of "ones" is $w_{\rm R}/n = w_{\rm C}/m$, so for large code word length $n$ the classification "low–density" is justified. For the red curve $(n = 2^{10})$ the share of "ones" is $0.6\%$.<br> | |
| − | |||
| − | |||
| − | |||
| − | + | *The rate of all codes is $R = 1 - w_{\rm C}/w_{\rm R} = 1/2$. However, because of the linear independence of the matrix rows, $R = k/n$ with the information word length $k = n - m = n/2$ also holds.<br><br> | |
| − | * | ||
| − | * | + | From the graph you can see: |
| + | *The bit error rate is smaller the longer the code: | ||
| + | :*For $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 2 \ \rm dB$ and $n = 2^8 = 256$ we get ${\rm BER} \approx 10^{-2}$. | ||
| + | :*For $n = 2^{12} = 4096$ on the other hand, only ${\rm BER} \approx 2 \cdot 10^{-7}$.<br> | ||
| − | * | + | *With $n = 2^{15} = 32768$ $($violet curve$)$ one needs $10 \cdot {\rm lg} \, E_{\rm B}/N_0 \approx 1.35 \ \rm dB$ for ${\rm BER} = 10^{-5}$. |
| + | |||
| + | *The distance from the Shannon bound $(0.18 \ \rm dB$ for $R = 1/2$ and BPSK$)$ is approximately $1.2 \ \rm dB$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:EN_KC_T_4_4_S4b_v1.png|left|frame| Waterfall region & error floor]] | |
| − | + | <br><br>The curves for $n = 2^8$ to $n = 2^{10}$ also point to an effect we already noticed with the [[Channel_Coding/The_Basics_of_Turbo_Codes#Performance_of_the_turbo_codes| $\text{turbo codes}$]] $($see qualitative graph on the left$)$: | |
| − | |||
| − | [[File: | ||
| − | |||
| − | + | #First, the BER curve drops steeply ⇒ "waterfall region". | |
| − | + | #That is followed by a kink and a course with a significantly lower slope ⇒ "error floor". | |
| − | + | #The graphic illustrates the effect, which of course does not start abruptly $($transition not drawn$)$.<br> | |
| − | + | An $($LDPC$)$ code is considered good whenever | |
| − | * | + | * the $\rm BER$ curve drops steeply near the Shannon bound,<br> |
| − | * | + | * the error floor is at very low $\rm BER$ values $($for causes see next section and $\text{Example 5)}$,<br> |
| − | * | + | * the number of required iterations is manageable, and<br> |
| − | * | + | * these properties are not reached only at no more practicable block lengths.<br> |
<br clear=all> | <br clear=all> | ||
| − | == | + | == Performance of irregular LDPC codes == |
<br> | <br> | ||
| − | [[File: | + | [[File:KC T 4 4 S5b v3.png|right|frame|LDPC codes compared <br>to the Shannon bound]] |
| − | + | This chapter has dealt mainly with regular LDPC codes, including in the $\rm BER$ diagram in the last section. The ignorance of irregular LDPC codes is only due to the brevity of this chapter, not their performance. | |
| − | * | + | |
| − | * | + | On the contrary: |
| − | * | + | * Irregular LDPC codes are among the best channel codes ever. |
| − | * | + | |
| + | *The yellow cross is practically on the information-theoretical limit curve for binary input signals $($green $\rm BPSK$ curve$)$. | ||
| + | |||
| + | *The code word length of this irregular rate $1/2$ code from [CFRU01]<ref>Chung S.Y; Forney Jr., G.D.; Richardson, T.J.; Urbanke, R.: On the Design of Low-Density Parity- Check Codes within 0.0045 dB of the Shannon Limit. - In: IEEE Communications Letters, vol. 5, no. 2 (2001), pp. 58-60.</ref> is $n = 2 \cdot 10^6$. | ||
| + | |||
| + | *From this it is already obvious that this code was not intended for practical use, but was even tuned for a record attempt:<br> | ||
| − | + | <u>Note:</u> | |
| + | #The LDPC code construction always starts from the parity-check matrix $\mathbf{H}$. | ||
| + | #For the just mentioned code this has the dimension $1 \cdot 10^6 × 2 \cdot 10^6$, thus contains $2 \cdot 10^{12}$ matrix elements. | ||
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ Filling the matrix randomly with $($few$)$ "ones" ⇒ "low–density" is called »<b>unstructured code design</b>«. |
| − | |||
| − | * | + | This can lead to long codes with good performance, but sometimes also to the following problems: |
| + | *The complexity of the encoder can increase, because despite modification of the parity-check matrix $\mathbf{H}$ it must be ensured that the generator matrix $\mathbf{G}$ is systematic.<br> | ||
| − | * | + | *It requires a complex hardware–realization of the iterative decoder.<br> |
| + | |||
| + | *It comes to an "error floor" by single "ones" in a column $($or row$)$ as well as by short loops ⇒ see following example.}}<br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5:}$ The left part of the graph shows the Tanner graph for a regular LDPC code with the parity-check matrix $\mathbf{H}_1$. |
| + | [[File:P ID3088 KC T 4 4 S4c v3.png|right|frame|Definition of a "girth"|class=fit]] | ||
| + | *Drawn in green is an example of the "minimum girth". | ||
| − | + | *This parameter indicates the minimum number of edges one passes through before ending up at a check node $C_j$ again $($or from $V_i$ to $V_i)$. | |
| − | + | *In the left example, the minimum edge length $6$, for example, results in the path | |
| − | + | :$$C_1 → V_1 → C_3 → V_5 → C_2 → V_2 → C_1.$$ | |
| − | |||
| − | == | + | ⇒ Swapping only two "ones" in the parity-check matrix ⇒ matrix $\mathbf{H}_2$, the LDPC code becomes irregular: |
| + | *The minimum loop length is now $4$, from | ||
| + | :$$C_1 → V_4 → C_4 → V_6 → C_1.$$ | ||
| + | *A small "girth" leads to a pronounced "error floor" in the BER process.}}<br> | ||
| + | |||
| + | == Some application areas for LDPC codes == | ||
<br> | <br> | ||
| − | [[File: | + | In the adjacent diagram, two communication standards based on structured $($regular$)$ LDPC codes are entered in comparison to the AWGN channel capacity.<br> |
| − | + | [[File:KC T 4 4 S5b v3.png|right|frame|Some standardized LDPC codes compared to the Shannon bound]] | |
| + | |||
| + | It should be noted that the bit error rate ${\rm BER}=10^{-5}$ is the basis for the plotted standardized codes, while the capacity curves $($according to information theory$)$ are for "zero" error probability. | ||
| + | |||
| + | ⇒ Red crosses indicate the »'''LDPC codes according to CCSDS'''« developed for distant space missions: | ||
| + | *This class provides codes of rate $1/3$, $1/2$, $2/3$ and $4/5$. | ||
| + | |||
| + | *All points are located $\approx 1 \ \rm dB$ to the right of the capacity curve for binary input $($green curve "BPSK"$)$.<br> | ||
| − | |||
| − | + | ⇒ The blue rectangles mark the »'''LDPC codes for DVB–T2/S2'''«. | |
| − | |||
| − | |||
| + | The abbreviations stand for "Digital Video Broadcasting – Terrestrial" resp. "Digital Video Broadcasting – Satellite", and the "$2$" marking makes it clear that each is the second generation $($from 2005 resp. 2009$)$. | ||
| + | *The standard is defined by $22$ test matrices providing rates from about $0.2$ up to $19/20$. | ||
| + | |||
| + | *Each eleven variants apply to the code length $n= 64800$ bit $($"Normal FECFRAME"$)$ and $16200$ bit $($"Short FECFRAME"$),$ respectively. | ||
| + | |||
| + | *Combined with [[Modulation_Methods/Quadrature_Amplitude_Modulation#Other_signal_space_constellations| $\text{high order modulation methods}$]] $($8PSK, 16–ASK/PSK, ... $)$ the codes are characterized by a large spectral efficiency.<br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ⇒ The "digital video broadcast" $\rm (DVB)$ codes belong to the "irregular repeat accumulate" $\rm (IRA)$ codes first presented in 2000 in [JKE00]<ref name='JKE00'>Jin, H.; Khandekar, A.; McEliece, R.: Irregular Repeat-Accumulate Codes. Proc. of the 2nd Int. Symp. on Turbo Codes and Related Topics, Brest, France, pp. 1-8, Sept. 2000.</ref>. The following graph shows the basic encoder structure: | |
| − | [[File: | + | [[File:EN_KC_T_4_4_S6a_v1.png|right|frame|Irregular Repeat Accumulate coder for DVB-S2/T2. Not taken into account in the graphic are <br> $\star$ LDPC codes for the standard "DVB Return Channel Terrestrial" $\rm (RCS)$, <br> $\star$ LDPC codes for the WiMax–standard $\rm (IEEE 802.16)$, as well as<br> $\star$ LDPC codes for "10GBASE–T–Ethernet".<br> These codes have certain similarities with the IRA codes.|class=fit]] |
| + | |||
| + | *The green highlighted part | ||
| + | :*with repetition code $\rm (RC)$, | ||
| + | :*interleaver, | ||
| + | :*single parity-check code $\rm (SPC)$, and | ||
| + | :*accumulator | ||
| − | + | :corresponds exactly to a serial–concatenated turbo code ⇒ see [[Channel_Coding/The_Basics_of_Turbo_Codes#Some_application_areas_for_turbo_codes| $\text{RA encoder}$]]. | |
| − | |||
| − | |||
| − | |||
| + | *The description of the "irregular repeat accumulate code" is based solely on the parity-check matrix $\mathbf{H}$, which can be transformed into a form favorable for decoding by the "irregular repetition code". | ||
| + | |||
| + | *A high-rate »'''BCH code'''« $($from $\rm B$ose–$\rm C$haudhuri–$\rm H$ocquenghem$)$ is often used as an outer encoder to lower the "error floor". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | == Exercises for the chapter == |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.11:_Analysis_of_Parity-check_Matrices|Exercise 4.11: Analysis of Parity-check Matrices]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.11Z:_Code_Rate_from_the_Parity-check_Matrix|Exercise 4.11Z: Code Rate from the Parity-check Matrix]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.12:_Regular_and_Irregular_Tanner_Graph|Exercise 4.12: Regular and Irregular Tanner Graph]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.13:_Decoding_LDPC_Codes|Exercise 4.13: Decoding LDPC Codes]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 18:10, 20 April 2023
Contents
Some characteristics of LDPC codes
The "Low–density Parity–check Codes" $($in short: »LDPC codes«$)$ were invented as early as the early 1960s and date back to the dissertation [Gal63][1] by $\text{Robert G. Gallager}$.
However, the idea came several decades too early due to the processor technology of the time. Only three years after Berrou's invention of the turbo codes in 1993, however, $\text{David J. C. MacKay}$ and $\text{Radford M. Neal}$ recognized the huge potential of the LDPC codes if they were decoded iteratively symbol by symbol just like the turbo codes. They virtually reinvented the LDPC codes.
As can already be seen from the name component "parity–check" that these codes are linear block codes according to the explanations in the "first main chapter" . Therefore, the same applies here:
- The code word results from the information word $\underline{u}$ $($represented with $k$ binary symbols$)$ and the $\text{generator matrix}$ $\mathbf{G}$ of dimension $k × n$ to $\underline{x} = \underline{u} \cdot \mathbf{G}$ ⇒ code word length $n$.
- The parity-check equations result from the identity $\underline{x} \cdot \mathbf{H}^{\rm T} ≡ 0$, where $\mathbf{H}$ denotes the parity-check matrix. This consists of $m$ rows and $n$ columns. While in the first chapter basically $m = n -k$ was valid, for the LPDC codes we only require $m ≥ n -k$.
- A serious difference between an LDPC code and a conventional block code as described in the first main chapter is that the parity-check matrix $\mathbf{H}$ is here sparsely populated with "ones" ⇒ "low-density".
$\text{Example 1:}$ The graph shows parity-check matrices $\mathbf{H}$ for
- the Hamming code with code length $n = 15$ and with $m = 4$ parity-check equations ⇒ $k = 11$ information bits,
- the LDPC code from [Liv15][2] of length $n = 12$ and with $m = 9$ parity-check equations ⇒ $k ≥ 3$ information bits.
Remarks:
- In the left graph, the proportion of "ones" is $32/60 \approx 53.3\%$.
- In the right graph the share of "ones" is lower with $36/108 = 33.3\%$.
- For LDPC codes $($relevant for practice ⇒ with long length$)$, the share of "ones" is even significantly lower.
We now analyze the two parity-check matrices using the rate and Hamming weight:
- The rate of the Hamming code under consideration $($left graph$)$ is $R = k/n = 11/15 \approx 0.733$. The Hamming weight of each of the four rows is $w_{\rm R}= 8$, while the Hamming weights $w_{\rm C}(i)$ of the columns vary between $1$ and $4$. For the columns index variable here: $1 ≤ i ≤ 15$.
- In the considered LDPC code there are four "ones" in all rows ⇒ $w_{\rm R} = 4$ and three "ones" in all columns ⇒ $w_{\rm C} = 3$. The code label $(w_{\rm R}, \ w_{\rm C})$ of LDPC code uses exactly these parameters. Note the different nomenclature to the "$(n, \ k, \ m)$ Hamming code".
- This is called a »regular LDPC code«, since all row weights $w_{\rm R}(j)$ for $1 ≤ j ≤ m$ are constant equal $w_{\rm R}$ and also all column weights $($with indices $1 ≤ i ≤ n)$ are equal: $w_{\rm C}(i) = w_{\rm C} = {\rm const.}$ If this condition is not met, there is an "irregular LDPC code".
$\text{Feature of LDPC codes}$
- For the code rate, one can generally $($if $k$ is not known$)$ specify only a bound:
- $$R ≥ 1 - w_{\rm C}/w_{\rm R}.$$
- The equal sign holds if all rows of $\mathbf{H}$ are linearly independent ⇒ $m = n \, – k$. Then the conventional equation is obtained:
- $$R = 1 - w_{\rm C}/w_{\rm R} = 1 - m/n = k/n.$$
- In contrast, for the code rate of an irregular LDPC code and also for the $(15, 11, 4)$ Hamming code sketched on the left:
- $$R \ge 1 - \frac{ {\rm E}[w_{\rm C}]}{ {\rm E}[w_{\rm R}]} \hspace{0.5cm}{\rm with}\hspace{0.5cm} {\rm E}[w_{\rm C}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm C}(i) \hspace{0.5cm}{\rm and}\hspace{0.5cm} {\rm E}[w_{\rm R}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm R}(j) \hspace{0.05cm}.$$
- In Hamming codes the $m = n - k$ parity-check equations are linearly independent, the "$≥$" sign can be replaced by the "$=$" sign, which simultaneously means:
- $$R = k/n.$$
For more information on this topic, see "Exercise 4.11" and "Exercise 4.11Z".
Two-part LDPC graph representation - Tanner graph
All essential features of a LDPC ode are contained in the parity-check matrix $\mathbf{H} = (h_{j,\hspace{0.05cm}i})$ and can be represented by a so-called "Tanner graph". It is a "bipartite graph representation". Before we examine and analyze exemplary Tanner graphs more exactly, first still some suitable description variables must be defined:
- The $n$ columns of the parity-check matrix $\mathbf{H}$ each represent one bit of a code word. Since each code word bit can be both an information bit and a parity bit, the neutral name »variable node « $\rm (VN)$ has become accepted for this. The $i$th code word bit is called $V_i$ and the set of all variable nodes is $\{V_1, \text{...}\hspace{0.05cm} , \ V_i, \ \text{...}\hspace{0.05cm} , \ V_n\}$.
- The $m$ rows of $\mathbf{H}$ each describe a parity-check equation. We refer to such a parity-check equation in the following as »check node« $\rm (CN)$. The set of all check nodes is $\{C_1, \ \text{...}\hspace{0.05cm} , \ C_j, \ \text{...}\hspace{0.05cm} , \ C_m\}$, where $C_j$ denotes the parity-check equation of the $j$th row.
- In the Tanner graph, the $n$ variable nodes $V_i$ are represented as circles and the $m$ check nodes $C_j$ as squares. If the $\mathbf{H}$ matrix element in row $j$ and column $i$ is $h_{j,\hspace{0.05cm}i} = 1$, there is an edge between the variable node $V_i$ and the check node $C_j$.
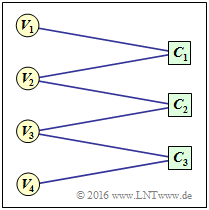
$\text{Example 2:}$ To clarify the above terms, an exemplary Tanner graph is given on the right with
- the variable nodes $V_1$ to $V_4$, and
- the check nodes $C_1$ to $C_3$.
However, the associated code has no practical meaning.
One can see from the graph:
- The code length is $n = 4$ and there are $m = 3$ parity-check equations.
- Thus the parity-check matrix $\mathbf{H}$ has dimension $3×4$.
- There are six edges in total. Thus six of the twelve elements $h_{j,\hspace{0.05cm}i}$ of matrix $\mathbf{H}$ are "ones".
- At each check node two lines arrive ⇒ the Hamming weights of all rows are equal: $w_{\rm R}(j) = 2 = w_{\rm R}$.
- From the nodes $V_1$ and $V_4$ there is only one transition to a check node each, from $V_2$ and $V_3$, however, there are two.
- For this reason, it is an "irregular code".
Accordingly, the parity-check matrix is:
- \[{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &1 &0 &0\\ 0 &1 &1 &0\\ 0 &0 &1 &1 \end{pmatrix}\hspace{0.05cm}.\]
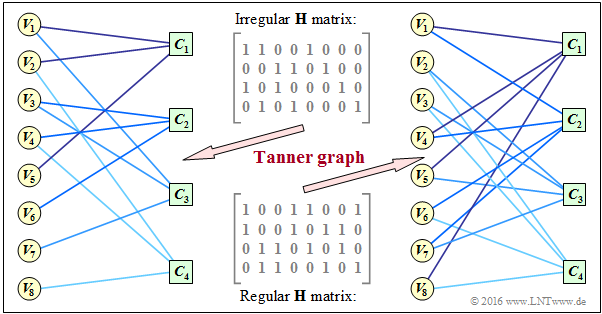
$\text{Example 3:}$ Now a more practical example follows. In "Exercise 4.11" two parity-check matrices were analyzed:
⇒ The encoder corresponding to the matrix $\mathbf{H}_1$ is systematic.
- The code parameters are $n = 8, \ k = 4,\ m = 4$ ⇒ rate $R=1/2$.
- The code is irregular because the Hamming weights are not the same for all columns.
- In the graph, this "irregular $\mathbf{H}$ matrix" is given above.
⇒ Bottom indicated is the "regular $\mathbf{H}$ matrix" corresponding to the matrix $\mathbf{H}_3$ from Exercise 4.11.
- The rows are linear combinations of the upper matrix $\mathbf{H}_1$.
- For this non-systematic encoder holds $w_{\rm C} = 2, \ w_{\rm R} = 4$.
- Thus for the rate: $R \ge 1 - w_{\rm C}/w_{\rm R} = 1/2$.
On the right you see the corresponding Tanner graphs:
- The left Tanner graph refers to the upper $($irregular$)$ matrix. The eight variable nodes $V_i$ are connected to the four check nodes $C_j$ if the element in row $j$ and column $i$ is a "one" $\hspace{0.15cm} ⇒ \hspace{0.15cm} h_{j,\hspace{0.05cm}i}=1$.
- This graph is not particularly well suited for $\text{iterative symbol-wise decoding}$. The variable nodes $V_5, \ \text{...}\hspace{0.05cm} , \ V_8$ are each associated with only one check node, which provides no information for decoding.
- In the right Tanner graph for the regular code, you can see that here from each variable node $V_i$ two edges come off and from each check node $C_j$ their four. This allows information to be gained during decoding in each iteration loop.
- It can also be seen that here, in the transition from the irregular to the equivalent regular code, the proportion of "ones" increases, in the example from $37.5\%$ to $50\%$. However, this statement cannot be generalized.
Iterative decoding of LDPC codes
As an example of iterative LDPC decoding, the so-called "message passing algorithm" is now described. We illustrate this using the right-hand Tanner graph in $\text{Example 3}$ in the previous section and thus for the regular parity-check matrix given there.
$\text{Principle:}$ In the »message passing algorithm« there is an alternating $($or iterative$)$ exchange of information between the variable nodes $V_1, \ \text{...}\hspace{0.05cm} , \ V_n$ and the check nodes $C_1 , \ \text{...}\hspace{0.05cm} , \ C_m$.
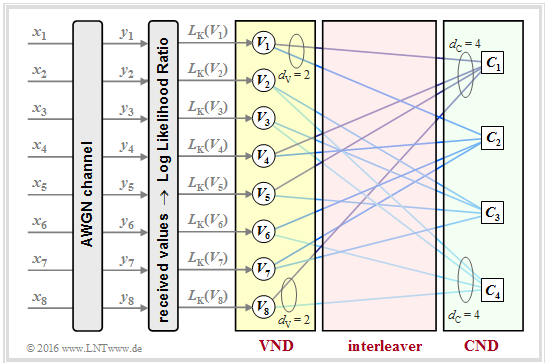
For the regular LDPC code under consideration:
- There are $n = 8$ variable nodes and $m = 4$ check nodes.
- From each variable node go $d_{\rm V} = 2$ connecting lines to a check node and each check node is connected to $d_{\rm C} = 4$ variable nodes.
- The variable node degree $d_{\rm V}$ is equal to the Hamming weight of each column $(w_{\rm C})$ and for the check node degree holds: $d_{\rm C} = w_{\rm R}$ (Hamming weight of each row).
- In the following description we use the terms "neighbors of a variable node" ⇒ $N(V_i)$ and "neighbors of a check node" ⇒ $N(C_j)$.
- We restrict ourselves here to implicit definitions:
- $$N(V_1) = \{ C_1, C_2\}\hspace{0.05cm},$$
- $$ N(V_2) = \{ C_3, C_4\},$$
- $$\text{........}$$
- $$N(V_8) = \{ C_1, C_4\},$$
- $$N(C_1) = \{ V_1, V_4, V_5, V_8\},$$
- $$\text{........}$$
- $$N(C_4) = \{ V_2, V_3, V_6, V_8\}.$$
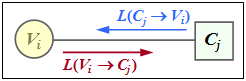
$\text{Example 4:}$The sketch from [Liv15][2] shows the information exchange
- between the yariable node $V_i$ and the check node $C_j$,
- expressed by $\text{log likelihood ratios}$ $(L$ values for short$)$.
The exchange of information happens in two directions:
- $L(V_i → C_j)$: Extrinsic information from $V_i$ point of view, a-priori information from $C_j$ point of view.
- $L(C_j → V_i)$: Extrinsic information from $C_j$ point of view, a-priori information from $V_i$ point of view.
The description of the decoding algorithm continues:
(1) Initialization: At the beginning of decoding, the variable nodes receive no a-priori information from the check nodes, and it applies for $1 ≤ i ≤ n \text{:}$
- $$L(V_i → C_j) = L_{\rm K}(V_i).$$
As can be seen from the graph at the top of the page, these channel log likelihood values $L_{\rm K}(V_i)$ result from the received values $y_i$.
(2) Check Node Decoder (CND): Each node $C_j$ represents one parity-check equation. Thus $C_1$ represents the equation $V_1 + V_4 + V_5 + V_8 = 0$. One can see the connection to extrinsic information in the symbol-wise decoding of the single parity–check code.
In analogy to the section "Calculation of extrinsic log likelihood ratios" and to "Exercise 4.4" thus applies to the extrinsic log likelihood value of $C_j$ and at the same time to the a-priori information concerning $V_i$:
- \[L(C_j \rightarrow V_i) = 2 \cdot {\rm tanh}^{-1}\left [ \prod\limits_{V \in N(C_j)\hspace{0.05cm},\hspace{0.1cm} V \ne V_i} \hspace{-0.35cm}{\rm tanh}\left [L(V \rightarrow C_j \right ] /2) \right ] \hspace{0.05cm}.\]
(3) Variable Node Decoder (VND): In contrast to the check node decoder, the variable node decoder is related to the decoding of a repetition code because all check nodes connected to $V_i$ correspond to the same bit $C_j$ ⇒ this bit is quasi repeated $d_{\rm V}$ times.
In analogy to to the section "Calculation of extrinsic log likelihood ratios" applies to the extrinsic log likelihood value of $V_i$ and at same time to the a-priori information concerning $C_j$:
- \[L(V_i \rightarrow C_j) = L_{\rm K}(V_i) + \hspace{-0.55cm} \sum\limits_{C \hspace{0.05cm}\in\hspace{0.05cm} N(V_i)\hspace{0.05cm},\hspace{0.1cm} C \hspace{0.05cm}\ne\hspace{0.05cm} C_j} \hspace{-0.55cm}L(C \rightarrow V_i) \hspace{0.05cm}.\]
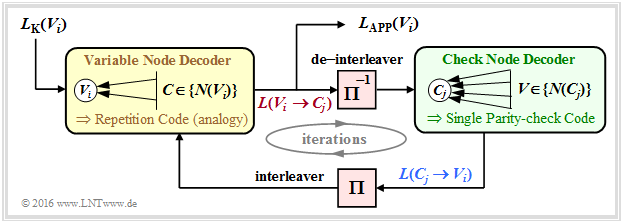
The chart on the right describes the decoding algorithm for LDPC codes.
- It shows similarities with the decoding method for $\text{serial concatenated turbo codes}$.
- To establish a complete analogy between LDPC and turbo decoding, an "interleaver" as well as a "de-interleaver" are also drawn here between $\rm VND$ and $\rm CND$.
- Since these are not real system components, but only analogies, we have enclosed these terms in quotation marks.
Performance of regular LDPC codes
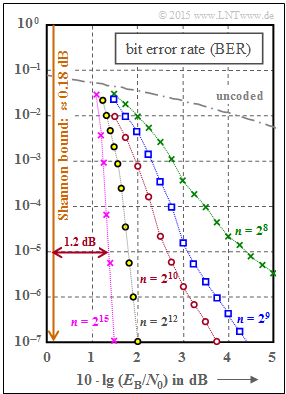
We now consider as in [Str14][3] five regular LDPC codes. The graph shows the bit error rate $\rm (BER)$ depending on the AWGN parameter $10 \cdot {\rm lg} \, E_{\rm B}/N_0$. The curve for uncoded transmission is also plotted for comparison.
These LDPC codes exhibit the following properties:
- The parity-check matrices $\mathbf{H}$ each have $n$ columns and $m = n/2$ linearly independent rows. In each row there are $w_{\rm R} = 6$ "ones" and in each column $w_{\rm C} = 3$ "ones".
- The share of "ones" is $w_{\rm R}/n = w_{\rm C}/m$, so for large code word length $n$ the classification "low–density" is justified. For the red curve $(n = 2^{10})$ the share of "ones" is $0.6\%$.
- The rate of all codes is $R = 1 - w_{\rm C}/w_{\rm R} = 1/2$. However, because of the linear independence of the matrix rows, $R = k/n$ with the information word length $k = n - m = n/2$ also holds.
From the graph you can see:
- The bit error rate is smaller the longer the code:
- For $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 2 \ \rm dB$ and $n = 2^8 = 256$ we get ${\rm BER} \approx 10^{-2}$.
- For $n = 2^{12} = 4096$ on the other hand, only ${\rm BER} \approx 2 \cdot 10^{-7}$.
- With $n = 2^{15} = 32768$ $($violet curve$)$ one needs $10 \cdot {\rm lg} \, E_{\rm B}/N_0 \approx 1.35 \ \rm dB$ for ${\rm BER} = 10^{-5}$.
- The distance from the Shannon bound $(0.18 \ \rm dB$ for $R = 1/2$ and BPSK$)$ is approximately $1.2 \ \rm dB$.
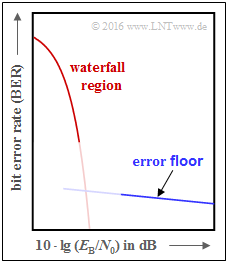
The curves for $n = 2^8$ to $n = 2^{10}$ also point to an effect we already noticed with the $\text{turbo codes}$ $($see qualitative graph on the left$)$:
- First, the BER curve drops steeply ⇒ "waterfall region".
- That is followed by a kink and a course with a significantly lower slope ⇒ "error floor".
- The graphic illustrates the effect, which of course does not start abruptly $($transition not drawn$)$.
An $($LDPC$)$ code is considered good whenever
- the $\rm BER$ curve drops steeply near the Shannon bound,
- the error floor is at very low $\rm BER$ values $($for causes see next section and $\text{Example 5)}$,
- the number of required iterations is manageable, and
- these properties are not reached only at no more practicable block lengths.
Performance of irregular LDPC codes
This chapter has dealt mainly with regular LDPC codes, including in the $\rm BER$ diagram in the last section. The ignorance of irregular LDPC codes is only due to the brevity of this chapter, not their performance.
On the contrary:
- Irregular LDPC codes are among the best channel codes ever.
- The yellow cross is practically on the information-theoretical limit curve for binary input signals $($green $\rm BPSK$ curve$)$.
- The code word length of this irregular rate $1/2$ code from [CFRU01][4] is $n = 2 \cdot 10^6$.
- From this it is already obvious that this code was not intended for practical use, but was even tuned for a record attempt:
Note:
- The LDPC code construction always starts from the parity-check matrix $\mathbf{H}$.
- For the just mentioned code this has the dimension $1 \cdot 10^6 × 2 \cdot 10^6$, thus contains $2 \cdot 10^{12}$ matrix elements.
$\text{Conclusion:}$ Filling the matrix randomly with $($few$)$ "ones" ⇒ "low–density" is called »unstructured code design«.
This can lead to long codes with good performance, but sometimes also to the following problems:
- The complexity of the encoder can increase, because despite modification of the parity-check matrix $\mathbf{H}$ it must be ensured that the generator matrix $\mathbf{G}$ is systematic.
- It requires a complex hardware–realization of the iterative decoder.
- It comes to an "error floor" by single "ones" in a column $($or row$)$ as well as by short loops ⇒ see following example.
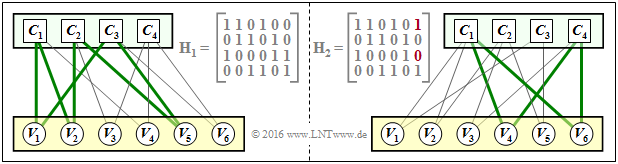
$\text{Example 5:}$ The left part of the graph shows the Tanner graph for a regular LDPC code with the parity-check matrix $\mathbf{H}_1$.
- Drawn in green is an example of the "minimum girth".
- This parameter indicates the minimum number of edges one passes through before ending up at a check node $C_j$ again $($or from $V_i$ to $V_i)$.
- In the left example, the minimum edge length $6$, for example, results in the path
- $$C_1 → V_1 → C_3 → V_5 → C_2 → V_2 → C_1.$$
⇒ Swapping only two "ones" in the parity-check matrix ⇒ matrix $\mathbf{H}_2$, the LDPC code becomes irregular:
- The minimum loop length is now $4$, from
- $$C_1 → V_4 → C_4 → V_6 → C_1.$$
- A small "girth" leads to a pronounced "error floor" in the BER process.
Some application areas for LDPC codes
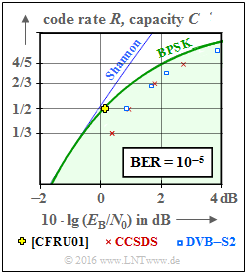
In the adjacent diagram, two communication standards based on structured $($regular$)$ LDPC codes are entered in comparison to the AWGN channel capacity.
It should be noted that the bit error rate ${\rm BER}=10^{-5}$ is the basis for the plotted standardized codes, while the capacity curves $($according to information theory$)$ are for "zero" error probability.
⇒ Red crosses indicate the »LDPC codes according to CCSDS« developed for distant space missions:
- This class provides codes of rate $1/3$, $1/2$, $2/3$ and $4/5$.
- All points are located $\approx 1 \ \rm dB$ to the right of the capacity curve for binary input $($green curve "BPSK"$)$.
⇒ The blue rectangles mark the »LDPC codes for DVB–T2/S2«.
The abbreviations stand for "Digital Video Broadcasting – Terrestrial" resp. "Digital Video Broadcasting – Satellite", and the "$2$" marking makes it clear that each is the second generation $($from 2005 resp. 2009$)$.
- The standard is defined by $22$ test matrices providing rates from about $0.2$ up to $19/20$.
- Each eleven variants apply to the code length $n= 64800$ bit $($"Normal FECFRAME"$)$ and $16200$ bit $($"Short FECFRAME"$),$ respectively.
- Combined with $\text{high order modulation methods}$ $($8PSK, 16–ASK/PSK, ... $)$ the codes are characterized by a large spectral efficiency.
⇒ The "digital video broadcast" $\rm (DVB)$ codes belong to the "irregular repeat accumulate" $\rm (IRA)$ codes first presented in 2000 in [JKE00][5]. The following graph shows the basic encoder structure:
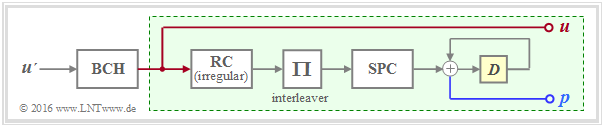
$\star$ LDPC codes for the standard "DVB Return Channel Terrestrial" $\rm (RCS)$,
$\star$ LDPC codes for the WiMax–standard $\rm (IEEE 802.16)$, as well as
$\star$ LDPC codes for "10GBASE–T–Ethernet".
These codes have certain similarities with the IRA codes.
- The green highlighted part
- with repetition code $\rm (RC)$,
- interleaver,
- single parity-check code $\rm (SPC)$, and
- accumulator
- corresponds exactly to a serial–concatenated turbo code ⇒ see $\text{RA encoder}$.
- The description of the "irregular repeat accumulate code" is based solely on the parity-check matrix $\mathbf{H}$, which can be transformed into a form favorable for decoding by the "irregular repetition code".
- A high-rate »BCH code« $($from $\rm B$ose–$\rm C$haudhuri–$\rm H$ocquenghem$)$ is often used as an outer encoder to lower the "error floor".
Exercises for the chapter
Exercise 4.11: Analysis of Parity-check Matrices
Exercise 4.11Z: Code Rate from the Parity-check Matrix
Exercise 4.12: Regular and Irregular Tanner Graph
Exercise 4.13: Decoding LDPC Codes
References
- ↑ Gallager, R. G.: Low-density parity-check codes. MIT Press, Cambridge, MA, 1963.
- ↑ 2.0 2.1 Liva, G.: Channels Codes for Iterative Decoding. Lecture notes, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2015.
- ↑ Strutz, T.: Low-density parity-check codes - An introduction. Lecture material. Hochschule für Telekommunikation, Leipzig, 2014. PDF document.
- ↑ Chung S.Y; Forney Jr., G.D.; Richardson, T.J.; Urbanke, R.: On the Design of Low-Density Parity- Check Codes within 0.0045 dB of the Shannon Limit. - In: IEEE Communications Letters, vol. 5, no. 2 (2001), pp. 58-60.
- ↑ Jin, H.; Khandekar, A.; McEliece, R.: Irregular Repeat-Accumulate Codes. Proc. of the 2nd Int. Symp. on Turbo Codes and Related Topics, Brest, France, pp. 1-8, Sept. 2000.