The Basics of Low-Density Parity Check Codes

1. Channel Coding
2. Iterative Decoding Methods
3. The Basics of Low-Density Parity Check Codes

• Previous page
• Next page

• Previous page
• Next page

Some characteristics of LDPC codes

The  Low–density Parity–check Codes  – in short  LDPC codes  – were invented as early as the early 1960s and date back to the dissertation  [Gal63] by  "Robert G. Gallager" .

However, the idea came several decades too early due to the processor technology of the time. Only three years after Berrou's invention of the turbo codes in 1993, however,  David J. C. MacKay  and  "Radford M. Neal"  recognized the huge potential of the LDPC codes if they were decoded iteratively symbol by symbol just like the turbo codes. They virtually reinvented the LDPC codes.

As can already be seen from the name component "parity–check", these codes are linear block codes according to the explanations in the  "first main chapter" . Therefore, the same applies here:

• The code word results from the information word  $\underline{u}$  (represented with  $k$  binary symbols) and the  "generator matrix"  $\mathbf{G}$  of dimension  $k × n$  to  $\underline{x} = \underline{u} \cdot \mathbf{G}$  ⇒   code word length  $n$.
  

• The parity-check equations result from the identity  $\underline{x} \cdot \mathbf{H}^{\rm T} ≡ 0$, where  $\mathbf{H}$  denotes the parity-check matrix. This consists of  $m$  rows and  $n$  columns. While in the first chapter basically  $m = n -k$  was valid, for the LPDC codes we only require  $m ≥ n -k$.
  
  

A serious difference between an LDPC code and a conventional block code as described in the first chapter is that the parity-check matrix  $\mathbf{H}$  is sparsely populated with ones  ("low-density').

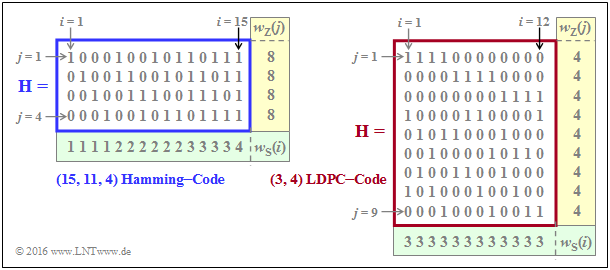
$\text{Example 1:}$  The graph shows parity-check matrices  $\mathbf{H}$  for

• the Hamming code with code length  $n = 15, \ m = 4$  ⇒   $k = 11$  information bits,
  

• the LDPC code from  [Liv15]  of length  $n = 12$  and with  $m = 9$  parity-check equations   ⇒   $k ≥ 3$.
  
  

Parity-check matrices of a Hamming code and a LDPC code

• In the left graph, the proportion of ones  $32/60 \approx is 53.3\%$, whereas in the right graph the share of ones is lower with  $36/108 = 33.3\%$ .
• For the LDPC codes (long length) relevant for practice, the share of ones is even significantly lower.
  

We now analyze the two parity-check matrices using the rate and Hamming weight:

• The rate of the Hamming code under consideration (left graph) is  $R = k/n = 11/15 \approx 0.733$. The Hamming weight of each of the four rows is  $w_{\rm Z}= 8$, while the Hamming weights  $w_{\rm S}(i)$  of the columns vary between 1 and 4. For the columns index variable here:   $1 ≤ i ≤ 15$.

• In the considered LDPC–code there are four ones in all rows   ⇒   $w_{\rm Z} = 4$  and three ones in all columns   ⇒   $w_{\rm S} = 3$. The code label  $(w_{\rm Z}, \ w_{\rm S})$  LDPC code uses exactly these parameters. Note the different nomenclature to the "$(n, \ k, \ m)$ Hamming code".

• This is called a  regular LDPC code, since all row weights  $w_{\rm Z}(j)$  for  $1 ≤ j ≤ m$  are constant equal  $w_{\rm Z}$ and also all column weights $($with the indices  $1 ≤ i ≤ n)$  are equal:   $w_{\rm S}(i) = w_{\rm S} = {\rm const.}$ If this condition is not met, there is an irregular LDPC code.

$\text{Feature of LDPC codes}$  For the code rate, one can generally  (if  $k$  is not known)  specify only one bound:  

$$R ≥ 1 - w_{\rm S}/w_{\rm Z}.$$

• The equal sign holds if all rows of  $\mathbf{H}$  are linearly independent   ⇒   $m = n \, – k$. Then the conventional equation is obtained:

$$R = 1 - w_{\rm S}/w_{\rm Z} = 1 - m/n = k/n.$$

• In contrast, for the code rate of an irregular LDPC code and also for the  $(15, 11, 4)$ Hamming code sketched on the left:

$$R \ge 1 - \frac{ {\rm E}[w_{\rm S}]}{ {\rm E}[w_{\rm Z}]} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm S}(i) \hspace{0.5cm}{\rm und}\hspace{0.5cm} {\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm Z}(j) \hspace{0.05cm}.$$

Since in Hamming code  the  $m = n - k$  parity-check equations are linearly independent, the  "$≥$"–sign can be replaced by the equal sign, which simultaneously means  $R = k/n$ .

For more information on this topic, see  "Exercise 4.11"  and  " Exercise 4.11Z".

Two-part LDPC graph representation - Tanner graph

All essential features of a LDPC ode are contained in the parity-check matrix  $\mathbf{H} = (h_{j,\hspace{0.05cm}i})$  and can be represented by a so-called  Tanner graph . It is a  Bipartite Graph Representation. Before we examine and analyze exemplary Tanner graphs more exactly, first still some suitable description variables must be defined:

• The  $n$  columns of the parity-check matrix  $\mathbf{H}$  each represent one code word bit. Since each code word bit can be both an information bit and a check bit, the neutral name  variable node  (VN) has become accepted for this. The  $i$th codeword bit is called  $V_i$  and the set of all  variable nodes  (VNs) is $\{V_1, \text{...}\hspace{0.05cm} , \ V_i, \ \text{...}\hspace{0.05cm} , \ V_n\}$.
  

• The  $m$  rows of  $\mathbf{H}$  each describe a parity-check equation. We refer to such a parity-check equation as  check node  (CN) in the following. The set of all  check nodes  (CNs) is  $\{C_1, \ \text{...}\hspace{0.05cm} , \ C_j, \ \text{...}\hspace{0.05cm} , \ C_m\}$, where  $C_j$  denotes the parity-check equation of the  $j$th row.
  

• In the Tanner–graph, the  $n$  variable nodes  $V_i$  as circles are represented as circles and the  $m$  check nodes  $C_j$ as squares. If the matrix element in row  $j$  and column  $i is \hspace{0.15cm} ⇒ \hspace{0.15cm} h_{j,\hspace{0.05cm}i} = 1$, there is an edge between the variable node  $V_i$  and the check node  $C_j$.
  
  

Simple example of a Tanner graph

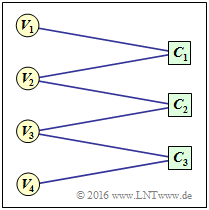
$\text{Example 2:}$  To clarify the above terms, an example Tanner graph is given on the right

• the Variable Nodes  (short:  VNs)  $V_1$  to  $V_4$, and
  
• the Check Nodes  (short:  CNs)  $C_1$  to  $C_3$.
  
  

However, the associated code has no practical meaning.

One can see from the graph:

• The code length is  $n = 4$  and there are  $m = 3$  parity-check equations. Thus the parity-check matrix  $\mathbf{H}$  has dimension  $3×4$.
  

• There are six edges in total. Thus six of the twelve elements  $h_{j,\hspace{0.05cm}i}$  are of  $\mathbf{H}$  ones.
  

• At each check node  two lines arrive   ⇒   The Hamming weights of all rows are equal:   $w_{\rm S}(j) = 2 = w_{\rm S}$.
  

• From nodes  $V_1$  and  $V_4$  there is only one transition to a check node each, from  $V_2$  nd  $V_3$  however, there are two.
  For this reason, it is an irregular code.
  
  

Accordingly, the parity-check matrix is:

\[{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &1 &0 &0\\ 0 &1 &1 &0\\ 0 &0 &1 &1 \end{pmatrix}\hspace{0.05cm}.\]

$\text{Example 3:}$  A more practical example now follows. In the  "Exercise 4.11"  two check matrices were analyzed:

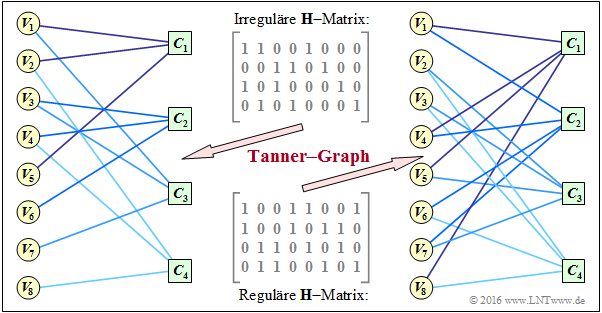
• The encoder corresponding to the matrix  $\mathbf{H}_1$  is systematic. The code parameters are  $n = 8, \ k = 4$  and  $m = 4$  ⇒   rate $1/2$. The code is irregular because the Hamming weights are not the same for all columns. In the graph, this "irregular  $\mathbf{H}$ matrix" is given above.
  

• Bottom indicated is the "regular  $\mathbf{H}$ matrix" corresponding to the matrix  $\mathbf{H}_3$  in exercise 4.11. The rows are linear combinations of the upper matrix. For this non-systematic coder, with  $w_{\rm S} = 2$  and  $w_{\rm Z} = 4$  for the rate:   $R \ge 1 - w_{\rm S}/w_{\rm Z} = 1/2$.

Tanner graph of a regular and an irregular code

The graph shows the corresponding Tanner–s graphs:

• The left graph refers to the upper (irregular) matrix. The eight variable nodes  (abbreviated VNs)  $V_i$  are connected to the four check nodes  (abbreviated CNs)  $C_j$  if the element in row  $j$  and column  $i \hspace{0.15cm} ⇒ \hspace{0.15cm} h_{j,\hspace{0.05cm}i}$  is equal  $1$ .
  

• This graph is not particularly well suited for  "iterative symbol-wise decoding" . The VNs  $V_5, \ \text{...}\hspace{0.05cm} , \ V_8$  are each associated with only one CN, which provides no information for decoding.
  

• In the right Tanner–s graph for the regular code, you can see that here from each variable node  $V_i$  two edges come off and from each check node  $C_j$  their four. This allows information to be gained during decoding in each iteration loop.
  

• It can also be seen that here, in the transition from the irregular to the equivalent regular code, the ones–share increases, in the example from  $37.5\%$  to $50\%$. However, this statement cannot be generalized.

Iterative decoding of LDPC codes

As an example of iterative LDPC–decoding, the so-called  message–passing algorithm  is now described. We illustrate this using the right-hand Tanner–graph in the  $\text{"Example 3"}$  on the previous page and thus for the regular parity-check matrix given there.

$\text{Principle:}$  In the  message–passing algorithm  there is an alternating (or iterative) exchange of information between the   (VNs)  $V_1, \ \text{...}\hspace{0.05cm} , \ V_n$  and the check nodes   (CNs)  $C_1 , \ \text{...}\hspace{0.05cm} , \ C_m$.

Iterative decoding of LDPC codes

For the example under consideration:

• There are  $n = 8$  variable nodes  and  $m = 4$  check nodes . Since there is a regular LDPC–code, connecting lines go from each variable node  $d_{\rm V} = 2$  to a check node   and each check node   is connected to  $d_{\rm C} = 4$  variable nodes.

• The variable node degree  $d_{\rm V}$  is equal to the Hamming weight of each column  $(w_{\rm S})$  and for the check node degree  holds:   $d_{\rm C} = w_{\rm Z}$ (Hamming weight of each row).

• In the following description we also use the terms neighbors of a variable node   ⇒   $N(V_i)$  and neighbors of a check node   ⇒   $N(C_j)$, restricting ourselves here to implicit definitions:

\[N(V_1) = \{ C_1, C_2\}\hspace{0.05cm}, \hspace{0.3cm}N(V_2) = \{ C_3, C_4\}\hspace{0.05cm}, \hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.15cm},\hspace{0.3cm}N(V_8) = \{ C_1, C_4\}\hspace{0.05cm},\]

\[N(C_1) = \{ V_1, V_4, V_5, V_8\}\hspace{0.05cm}, \hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.15cm}\hspace{0.05cm}, \hspace{0.3cm}N(C_4) = \{ V_2, V_3, V_6, V_8\}\hspace{0.05cm}.\]

Information exchange between variable nodes  and check nodes .

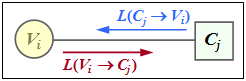
$\text{Example 4:}$  $\text{Example 4:}$  Die Skizze aus  [Liv15]  shows the exchange of information between the Variable Node  $V_i$  and the Check Node  $C_j$  – expressed by  "Log–Likelihood Ratios"  ($L$ values for short).

The exchange of information happens in two directions:

• $L(V_i → C_j)$:  Extrinsic information from  $V_i$–point of view,  a priori–information from  $C_j$–point of view.
  

• $L(C_j → V_i)$:  Extrinsic information from  $C_j$–point of view,  a priori–information from  $V_i$–point of view.

The description of the decoding algorithm continues:

Initialization:  At the beginning of decoding, the variable nodes  (VNs) receive no a priori–information from the check nodes  (CNs), and it applies to  $1 ≤ i ≤ n \text{:}$  

$$L(V_i → C_j) = L_{\rm K}(V_i).$$

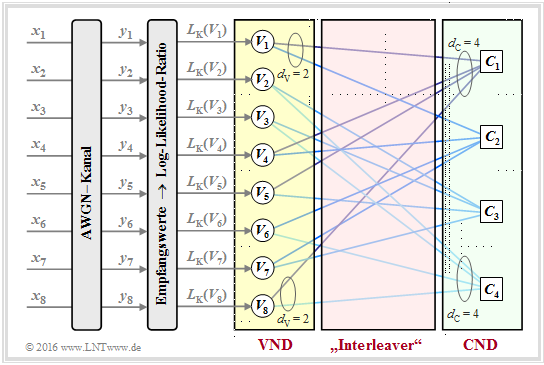
As can be seen from the graph at the top of the page, these channel–$L$ values  $L_{\rm K}(V_i)$  result from the received values  $y_i$.

Check Node Decoder:  Each node  $C_j$  represents a parity-check equation. Thus  $C_1$  represents the equation  $V_1 + V_4 + V_5 + V_8 = 0$. One can see the connection to extrinsic information in the symbol-wise decoding of the Single Parity–check Code.

In analogy to the page  "To calculate the extrinsic L–values"  and to the  "Exercise 4.4"  thus applies to the extrinsic  $L$–value of  $C_j$  and at the same time to the a priori information concerning  $V_i$:

\[L(C_j \rightarrow V_i) = 2 \cdot {\rm tanh}^{-1}\left [ \prod\limits_{V \in N(C_j)\hspace{0.05cm},\hspace{0.1cm} V \ne V_i} \hspace{-0.35cm}{\rm tanh}\left [L(V \rightarrow C_j \right ] /2) \right ] \hspace{0.05cm}.\]

Variable Node Decoder:  In contrast to the check node decoder  (CND), the variable node decoder  (VND) is related to the decoding of a repetition code because all check nodes connected to  $V_i$  correspond to the same bit  $C_j$  ⇒   this bit is repeated quasi  $d_{\rm V}$  times.

In analogy to to the page  "To calculate the extrinsic L values"  applies to the extrinsic  $L$ value of  $V_i$  and at the same time to the a priori information concerning  $C_j$:

\[L(V_i \rightarrow C_j) = L_{\rm K}(V_i) + \hspace{-0.55cm} \sum\limits_{C \hspace{0.05cm}\in\hspace{0.05cm} N(V_i)\hspace{0.05cm},\hspace{0.1cm} C \hspace{0.05cm}\ne\hspace{0.05cm} C_j} \hspace{-0.55cm}L(C \rightarrow V_i) \hspace{0.05cm}.\]

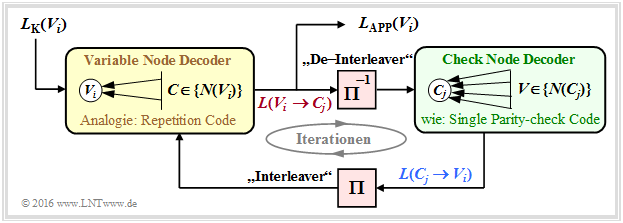
The following diagram of the described decoding algorithm for LDPC–codes shows similarities with the procedure for  "serial concatenated turbo codes".

Relationship between LDPC decoding and serial turbo decoding

• To establish a complete analogy between the LDPC and turbo decoding, an "interleaver "  as well as an "deinterleaver "  are also drawn here between the variable node decoder  (VND) and the check node decoder  (CND).
• Since these are not real system components, but only analogies, we have enclosed these terms in quotation marks.
  

Performance of regular LDPC codes

Bit error rate of LDPC codes

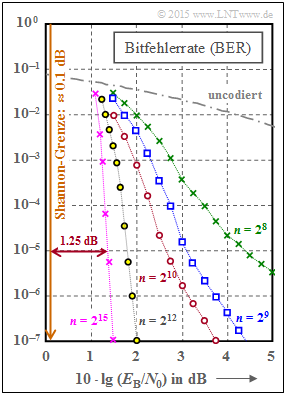
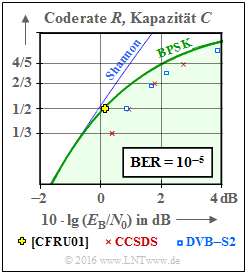
We now consider as in  [Str14]  five regular LDPC codes. The graph shows the bit error rate  $\rm (BER)$  depending on the AWGN parameter  $10 \cdot {\rm lg} \, E_{\rm B}/N_0$. The curve for uncoded transmission is also plotted for comparison.

Diese LDPC–Codes zeigen folgende Eigenschaften:

• Die Prüfmatrizen  $\mathbf{H}$  weisen jeweils  $n$  Spalten und  $m = n/2$  linear voneinander unabhängige Zeilen auf. In jeder Zeile gibt es  $w_{\rm Z} = 6$  Einsen und in jeder Spalte  $w_{\rm S} = 3$  Einsen.
  

• Der Einsen–Anteil beträgt  $w_{\rm Z}/n = w_{\rm S}/m$, so dass bei großer Codewortlänge  $n$  die Klassifizierung "Low–density" gerechtfertigt ist. Für die rote Kurve  $(n = 2^{10})$  beträgt der Einsen–Anteil  $0.6\%$.
  

• Die Rate aller Codes beträgt  $R = 1 - w_{\rm S}/w_{\rm Z} = 1/2$. Wegen der linearen Unabhängigkeit der Matrixzeilen gilt aber auch  $R = k/n$  mit der Informationswortlänge  $k = n - m = n/2$.
  
  

Aus der Grafik erkennt man:

• Die Bitfehlerrate ist um so kleiner, je länger der Code ist:

• Für  $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 2 \ \rm dB$  und  $n = 2^8 = 256$  ergibt sich  ${\rm BER} \approx 10^{-2}$.
• Für  $n = 2^{12} = 4096$  dagegen nur  ${\rm BER} \approx 2 \cdot 10^{-7}$.
  

• Mit  $n = 2^{15} = 32768$  (violette Kurve) benötigt man  $10 \cdot {\rm lg} \, E_{\rm B}/N_0 \approx 1.35 \ \rm dB$  für  ${\rm BER} = 10^{-5}$.
• Der Abstand von der Shannon–Grenze  $(0.18 \ \rm dB$  für  $R = 1/2$  und BPSK$)$ beträgt ca.  $1.2 \ \rm dB$.

"Waterfall Region & Error Floor"

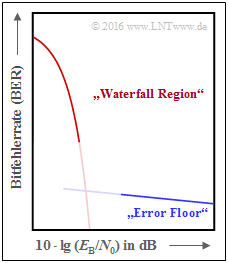
Die Kurven für  $n = 2^8$  bis  $n = 2^{10}$  weisen zudem auf einen Effekt hin, den wir schon bei den  "Turbocodes"  festgestellt haben:

• Zuerst fällt die BER–Kurve steil ab   ⇒   "Waterfall Region".
• Danach folgt ein Knick und ein Verlauf mit deutlich geringerer Steigung   ⇒   "Error Floor".
• Die qualitative untere Grafik verdeutlicht den Effekt, der natürlich nicht abrupt einsetzt (Übergang nicht eingezeichnet).
  

Ein (LDPC–) Code ist immer dann als gut zu bezeichnen, wenn

• die BER–Kurve nahe der Shannon–Grenze steil abfällt,
  

• der "Error Floor" bei sehr niedrigen BER–Werten liegt (Ursachen hierfür siehe nächste Seite,  $\text{Beispiel 5)}$,
  

• die Anzahl der erforderlichen Iterationen handhabbar ist, und
  

• diese Eigenschaften nicht erst bei nicht mehr praktikablen Blocklängen erreicht werden.
  

Leistungsfähigkeit irregulärer LDPC–Codes

LDPC–Codes im Vergleich zur Shannon–Grenze

In diesem Kapitel wurden vorwiegend reguläre LDPC–Codes behandelt, auch im  $\rm BER$–Diagramm auf der letzten Seite. Die Ignoranz der irregulären LDPC–Codes ist nur der Kürze dieses Kapitels geschuldet, nicht deren Leistungsfähigkeit. Im Gegenteil:

• Irreguläre LDPC–Codes gehören zu den besten Kanalcodes überhaupt.
• Das gelbe Kreuz in der Grafik liegt praktisch auf der informationstheoretischen Grenzkurve für binäre Eingangssignale (grüne Kurve, mit  $\rm BPSK$ beschriftet).
• Die Codewortlänge dieses irregulären Rate–$1/2$–Codes von [CFRU01] beträgt  $n = 2 \cdot 10^6$.
• Daraus ist schon ersichtlich, dass dieser Code nicht für den praktischen Einsatz gedacht war, sondern sogar für einen Rekordversuch getunt wurde.
  

Bei der LDPC–Codekonstruktion geht man ja stets von der Prüfmatrix  $\mathbf{H}$  aus. Für den gerade genannten Code hat diese die Dimension  $1 \cdot 10^6 × 2 \cdot 10^6$, beinhaltet also  $2 \cdot 10^{12}$  Matrixelemente.

$\text{Fazit:}$  Füllt man die Matrix per Zufallsgenerator mit (wenigen) Einsen   ⇒   "Low–density", so spricht man von  unstrukturiertem Code–Design. Dies kann zu langen Codes mit guter Performance führen, manchmal aber auch zu folgenden Problemen:

• Die Komplexität des Coders kann zunehmen, da trotz Modifikation der Prüfmatrix  $\mathbf{H}$  sichergestellt werden muss, dass die Generatormatrix  $\mathbf{G}$  systematisch ist.
  

• Es erfordert eine aufwändige Hardware–Realisierung des iterativen Decoders.
  

• Es kommt zu einem "Error Floor" durch einzelne Einsen in einer Spalte (oder Zeile) sowie durch kurze Schleifen   ⇒   siehe nachfolgendes Beispiel.

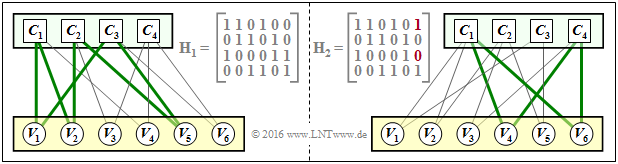
$\text{Beispiel 5:}$  Im linken Teil der Grafik ist der Tanner–Graph für einen regulären LDPC–Code mit der Prüfmatrix  $\mathbf{H}_1$  dargestellt. Grün eingezeichnet ist ein Beispiel für die minimale Schleifenlänge (englisch:  Girth). Diese Kenngröße gibt an, wieviele Kanten man mindestens durchläuft, bis man von einem Check Node  $C_j$  wieder bei diesem landet $($oder von  $V_i$  zu  $V_i)$. Im linken Beispiel ergibt sich die minimale Kantenlänge  $6$, zum Beispiel der Weg  $C_1 → V_1 → C_3 → V_5 → C_2 → V_2 → C_1$.

Zur Definition eines „Girth”

Vertauscht man in der Prüfmatrix nur zwei Einsen   ⇒   Matrix  $\mathbf{H}_2$, so wird der LDPC–Code irregulär:

• Die minimale Schleifenlänge ist nun  $4$, von  $C_1 → V_4 → C_4 → V_6 → C_1$.
• Ein kleiner Girth  führt zu einem ausgeprägten "Error Floor" im BER–Verlauf.

Einige Anwendungsgebiete für LDPC–Codes

Einige standardisierte LDPC–Codes im Vergleich zur Shannon–Grenze

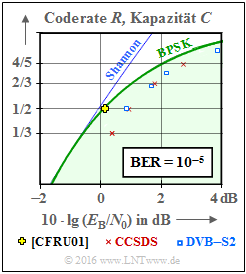
Im nebenstehenden Schaubild sind im Vergleich zur AWGN–Kanalkapazität zwei Kommunikations–Standards eingetragen, die auf strukturierten (regulären) LDPC–Codes basieren.

Anzumerken ist, dass für die eingezeichneten standardisierten Codes die Bitfehlerrate ${\rm BER}=10^{-5}$ zugrunde liegt, während die Kapazitätskurven (entsprechend der Informationstheorie) für die Fehlerwahrscheinlichkeit "Null" gelten.

Rote Kreuze zeigen die  LDPC–Codes nach CCSDS  (Consultative Comittee for Space Data Systems), entwickelt für ferne Weltraummissionen:

• Diese Klasse stellt Codes der Rate  $1/3$,  $1/2$,  $2/3$  und  $4/5$ bereit.
• Alle Punkte liegen ca.  $1 \ \rm dB$  rechts von der Kapazitätskurve für binären Eingang (grüne Kurve "BPSK").
  

Die blauen Rechtecke markieren die  LDPC–Codes für DVB–T2/S2. Die Abkürzungen stehen für "Digital Video Broadcasting – Terrestrial" bzw. "Digital Video Broadcasting – Satellite", und die Kennzeichnung "$2$" macht deutlich, dass es sich jeweils um die zweite Generation (von 2005 bzw. 2009) handelt.

• Der Standard ist durch  $22$  Prüfmatrizen definiert, die Raten von etwa  $0.2$  bis zu  $19/20$  zur Verfügung stellen.
• Je elf Varianten gelten für die Codelänge  $64800$  Bit (Normal FECFRAME) bzw.  $16200$  Bit (Short FECFRAME).
• Kombiniert mit  "Modulationsverfahren hoher Ordnung"  (8PSK, 16–ASK/PSK, ... ) zeichnen sich die Codes durch eine große spektrale Effizienz aus.
  

Die DVB–Codes gehören zu den  Irregular Repeat Accumulate  $\rm (IRA)$ Codes, die erstmals im Jahr 2000 in  [JKE00]  vorgestellt wurden.

IRA–Coder bei DVB–S2/T2

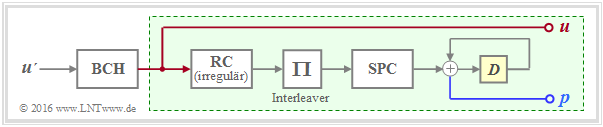
Die Grafik zeigt die Grundstruktur des Coders.

• Der grün hinterlegte Teil – mit Repetition Code  $\rm (RC)$, Interleaver, Single Parity–Code  $\rm (SPC)$  sowie Akkumulator – entspricht exakt einem seriell–verketteten Turbocode   ⇒   siehe  "RA–Coder".
• Die Beschreibung des IRA–Codes basiert aber allein auf der Prüfmatrix  $\mathbf{H}$, die sich durch den  irregulären Repetition Code  in eine für die Decodierung günstige Form bringen lässt.
• Als äußerer Code wird zudem ein hochratiger BCH–Code (von $\rm B$ose–$\rm C$haudhuri–$\rm H$ocquenghem) verwendet, der den  Error Floor  herabsetzen soll.
  

In der Grafik am Seitenanfang nicht eingetragen sind

• die LDPC–Codes für den Standard  DVB Return Channel Terrestrial (RCS),
• die LDPC–Codes für den WiMax–Standard  (IEEE 802.16), sowie
• die LDPC–Codes für das  10GBASE–T–Ethernet,

die gewisse Ähnlichkeiten mit den IRA–Codes aufweisen.

Aufgaben zum Kapitel

Aufgabe 4.11: Analyse von Prüfmatrizen

Zusatzaufgabe 4.11Z: Coderate aus der Prüfmatrix

Aufgabe 4.12: Regulärer/irregulärer Tanner–Graph

Aufgabe 4.13: Decodierung von LDPC–Codes