Difference between revisions of "Digital Signal Transmission/Error Probability with Intersymbol Interference"
| Line 66: | Line 66: | ||
*The Gaussian low-pass filter $H_{\rm G}(f)$ causes the detection pulse $g_d(t)$ to be reduced and broadened compared to the transmitted pulse $g_s(t)$ ⇒ ''time dispersion''.<br> | *The Gaussian low-pass filter $H_{\rm G}(f)$ causes the detection pulse $g_d(t)$ to be reduced and broadened compared to the transmitted pulse $g_s(t)$ ⇒ ''time dispersion''.<br> | ||
| − | * | + | *This pulse deformation is the stronger, the smaller the cutoff frequency $f_{\rm G}$ is. For example, with $f_{\rm G} \cdot T = 0.4$ (red curve) the pulse maximum is already reduced to about $68\%$. <br> |
| − | * | + | *In the limiting case $f_{\rm G} \to \infty$ the Gaussian low-pass has no effect ⇒ $g_d(t) = g_s(t)$. However, in this case, no noise limitation is effective at all, as can be seen from the right figure.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ The same preconditions apply as for the last example. The graph shows the detection signal $d(t)$ after the Gaussian low-pass (before the decision) for two different cutoff frequencies, namely $f_{\rm G} \cdot T = 0.8$ and $f_{\rm G} \cdot T = 0.4$ |
| − | [[File:P ID1384 Dig T 3 2 S1c version2.png|center|frame| | + | [[File:P ID1384 Dig T 3 2 S1c version2.png|center|frame|Detection signal with Gaussian receiver filter]] |
| − | + | Shown equally in both diagrams (but admittedly difficult to see as a screen capture) are: | |
| − | * | + | *the component $d_{\rm S}(\nu \cdot T)$ without considering the noise (blue circles at the detection times),<br> |
| − | * | + | *the total detection signal $d(t)$ including the noise component (yellow),<br> |
| − | * | + | *the transmitted signal $s(t)$ as reference signal (green dotted in the upper graph; equally valid for the lower graph).<br><br> |
| − | + | By comparing these images, the following statements can be verified: | |
| − | * | + | *With the cutoff frequency $f_{\rm G} \cdot T = 0.8$ (upper graph), only minorintersymbol interferences result at the detection times $($at multiples of $T)$. Due to the Gaussian low-pass here primarily the corners of the transmitted signal $s(t)$ are rounded.<br> |
| − | * | + | *In contrast, in the lower image $(f_{\rm G} \cdot T = 0.4)$ die Auswirkungen der Impulsinterferenzen deutlich zu erkennen. Zu den Detektionszeitpunkten $(\nu \cdot T)$ kann das blau dargestellte Detektionsnutzsignal $d_{\rm S}(\nu \cdot T)$ sechs verschiedene Werte annehmen (eingezeichnete Rasterlinien).<br> |
*Der Rauschanteil $d_{\rm N}(t)$ – erkennbar als Differenz zwischen der gelben Kurve und den blauen Kreisen – ist mit $f_{\rm G} \cdot T = 0.8$ im statistischen Mittel größer als mit $f_{\rm G} \cdot T = 0.4$.<br> | *Der Rauschanteil $d_{\rm N}(t)$ – erkennbar als Differenz zwischen der gelben Kurve und den blauen Kreisen – ist mit $f_{\rm G} \cdot T = 0.8$ im statistischen Mittel größer als mit $f_{\rm G} \cdot T = 0.4$.<br> | ||
*Dieses Ergebnis kann mit der der rechten Grafik von $\text{Beispiel 1}$ erklärt werden, die das Leistungsdichtespektrum der Rauschkomponente $d_{\rm N}(t)$ zeigt: | *Dieses Ergebnis kann mit der der rechten Grafik von $\text{Beispiel 1}$ erklärt werden, die das Leistungsdichtespektrum der Rauschkomponente $d_{\rm N}(t)$ zeigt: | ||
Revision as of 15:50, 25 April 2022
Contents
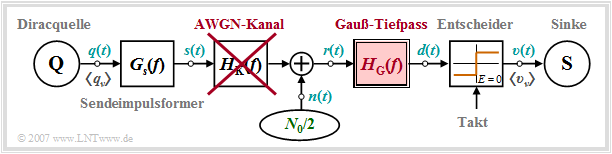
Gaussian receiver filter
We start from the sketched block diagram. The following configuration is assumed for quantitative consideration of the intersymbol interference:
- Rectangular NRZ basic transmission pulse $g_s(t)$ with height $s_0$ and duration $T$,
- Gaussian-shaped receiver filter with cutoff frequency $f_{\rm G}$ (Note: In this section, we often also denote the exponential function by $\rm exp [ . ]$):
- $$H_{\rm E}(f) = H_{\rm G}(f) = {\rm exp}\left [- \frac{\pi \cdot f^2}{(2f_{\rm G})^2} \right ] \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm}h_{\rm E}(t) = h_{\rm G}(t) = {\rm exp}\left [- \pi \cdot (2 f_{\rm G} t)^2\right ] \hspace{0.05cm}.$$
- AWGN channel, that is, $H_{\rm K}(f) = 1 $ and ${\it \Phi}_n(f) = N_0/2$.
Based on the assumptions made here, the following holds for the basic detection pulse:
- $$g_d(t) = g_s(t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot s_0 \cdot \int_{t-T/2}^{t+T/2} {\rm e}^{- \pi \hspace{0.05cm}\cdot\hspace{0.05cm} (2 \hspace{0.05cm}\cdot\hspace{0.05cm} f_{\rm G}\hspace{0.05cm}\cdot\hspace{0.05cm} \tau )^2} \,{\rm d} \tau \hspace{0.05cm}.$$
The integration leads to the following equivalent results:
- $$g_d(t) = s_0 \cdot \big [ {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \big ],$$
- $$g_d(t) = s_0 \cdot\big [ {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \big ]\hspace{0.05cm}.$$
Here, two variants of the complementary Gaussian error function are used, viz.
- $${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} \hspace{0.05cm},\hspace{0.5cm} {\rm erfc} (\it x) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$
The module Complementary Gaussian Error Functions provides the numerical values of ${\rm Q} (x)$ and $0.5 \cdot {\rm erfc} (x)$.
The noise power at the output of the Gaussian receiver filter $H_{\rm G}(f)$ is equal to
- $$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0\cdot f_{\rm G}}{\sqrt{2}}\hspace{0.05cm}.$$
From these two equations one can already see:
- The smaller the cutoff frequency $f_{\rm G}$ of the Gaussian low-pass filter, the smaller the noise rms value $\sigma_d$ and consequently the better the noise performance.
- However, a small cutoff frequency leads to a strong deviation of the basic detection pulse $g_d(t)$ from the square wave form and thus to intersymbol interference.
$\text{Example 1:}$ The left graph shows the basic detection pulse $g_d(t)$ at the output of a Gaussian low-pass filter $H_{\rm G}(f)$ with the cutoff frequency $f_{\rm G}$ when an NRZ rectangular pulse (blue curve) is applied at the input.
One can see from this plot:
- The Gaussian low-pass filter $H_{\rm G}(f)$ causes the detection pulse $g_d(t)$ to be reduced and broadened compared to the transmitted pulse $g_s(t)$ ⇒ time dispersion.
- This pulse deformation is the stronger, the smaller the cutoff frequency $f_{\rm G}$ is. For example, with $f_{\rm G} \cdot T = 0.4$ (red curve) the pulse maximum is already reduced to about $68\%$.
- In the limiting case $f_{\rm G} \to \infty$ the Gaussian low-pass has no effect ⇒ $g_d(t) = g_s(t)$. However, in this case, no noise limitation is effective at all, as can be seen from the right figure.
$\text{Example 2:}$ The same preconditions apply as for the last example. The graph shows the detection signal $d(t)$ after the Gaussian low-pass (before the decision) for two different cutoff frequencies, namely $f_{\rm G} \cdot T = 0.8$ and $f_{\rm G} \cdot T = 0.4$
Shown equally in both diagrams (but admittedly difficult to see as a screen capture) are:
- the component $d_{\rm S}(\nu \cdot T)$ without considering the noise (blue circles at the detection times),
- the total detection signal $d(t)$ including the noise component (yellow),
- the transmitted signal $s(t)$ as reference signal (green dotted in the upper graph; equally valid for the lower graph).
By comparing these images, the following statements can be verified:
- With the cutoff frequency $f_{\rm G} \cdot T = 0.8$ (upper graph), only minorintersymbol interferences result at the detection times $($at multiples of $T)$. Due to the Gaussian low-pass here primarily the corners of the transmitted signal $s(t)$ are rounded.
- In contrast, in the lower image $(f_{\rm G} \cdot T = 0.4)$ die Auswirkungen der Impulsinterferenzen deutlich zu erkennen. Zu den Detektionszeitpunkten $(\nu \cdot T)$ kann das blau dargestellte Detektionsnutzsignal $d_{\rm S}(\nu \cdot T)$ sechs verschiedene Werte annehmen (eingezeichnete Rasterlinien).
- Der Rauschanteil $d_{\rm N}(t)$ – erkennbar als Differenz zwischen der gelben Kurve und den blauen Kreisen – ist mit $f_{\rm G} \cdot T = 0.8$ im statistischen Mittel größer als mit $f_{\rm G} \cdot T = 0.4$.
- Dieses Ergebnis kann mit der der rechten Grafik von $\text{Beispiel 1}$ erklärt werden, die das Leistungsdichtespektrum der Rauschkomponente $d_{\rm N}(t)$ zeigt:
- $${\it \Phi}_{d{\rm N} }(f) = {N_0}/{2} \cdot \vert H_{\rm G}(f) \vert^2 = {N_0}/{2} \cdot {\rm exp}\left [- \frac{2\pi f^2}{(2f_{\rm G})^2} \right ] .$$
- Das Integral über ${\it \Phi}_{d{\rm N} }(f)$ – also die Rauschleistung $\sigma_d^2$ – ist für $f_{\rm G} \cdot T = 0.8$ (violette Kurve) doppelt so groß als mit $f_{\rm G} \cdot T = 0.4$ (rote Kurve).
Definition and statements of the eye diagram
Der oben dargelegte Sachverhalt lässt sich auch am Augendiagramm erklären.
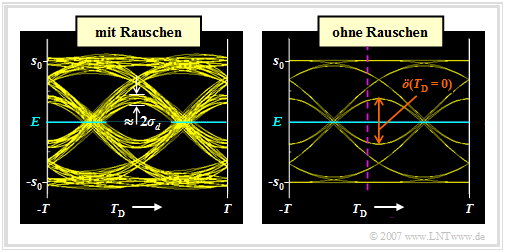
$\text{Definition:}$ Unter dem Augendiagramm (Englisch: Eye Pattern) versteht man die Summe aller übereinander gezeichneten Ausschnitte des Detektionssignals, deren Dauer ein ganzzahliges Vielfaches der Symboldauer $T$ ist.
$\text{Beispiel 3:}$ Wir gehen von einem redundanzfreien binären bipolaren NRZ–Rechtecksignal $s(t)$ und dem Gaußtiefpass mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.4$ aus.
Dargestellt sind die Augendiagramme nach dem Gaußtiefpass,
- links mit Berücksichtigung des Rauschens ⇒ Signal $d(t)$,
- rechts ohne Berücksichtigung des Rauschens ⇒ Signal $d_{\rm S}(t)$.
Dieses Diagramm hat eine gewisse Ähnlichkeit mit einem Auge, was zu seiner Namensgebung geführt hat.
Diese Darstellung erlaubt wichtige Aussagen über die Qualität eines digitalen Übertragungssystems:
- Nur das Augendiagramm des Signals $d(t)$ kann messtechnisch auf einem Oszilloskop dargestellt werden, das mit dem Taktsignal getriggert wird. Aus diesem Augendiagramm (linke Grafik) kann beispielsweise der Rauscheffektivwert $\sigma_d$ abgelesen – besser gesagt: abgeschätzt – werden.
- Das Augendiagramm ohne Rauschen (rechte Grafik) bezieht sich auf das Detektionsnutzsignal $d_{\rm S}(t)$ und kann nur mittels einer Rechnersimulation ermittelt werden. Für ein realisiertes System ist dieses Augendiagramm nicht darstellbar, da der Rauschanteil $d_{\rm N}(t)$ nicht eliminiert werden kann.
- Bei beiden Diagrammen wurden jeweils $2048$ Augenlinien gezeichnet. In der rechten Grafik sind jedoch nur $2^5 = 32$ Augenlinien unterscheidbar, da der vorliegende Detektionsgrundimpuls $g_d(t)$ auf den Zeitbereich $\vert t\vert \le 2T$ beschränkt ist (siehe Grafik im Beispiel 1 mit $f_{\rm G} \cdot T = 0.4$, rote Kurve).
- Die inneren Augenlinien bestimmen die vertikale Augenöffnung $\ddot{o}(T_{\rm D})$. Je kleiner diese ist, desto größer ist der Einfluss von Impulsinterferenzen. Bei einem (impulsinterferenzfreien) Nyquistsystem ist die vertikale Augenöffnung maximal. Normiert auf die Sendeamplitude gilt dann $\ddot{o}(T_{\rm D})/s_0 = 2$.
- Bei symmetrischem Grundimpuls ist der Detektionszeitpunkt $T_{\rm D} = 0$ optimal. Mit einem anderen Wert $($zum Beispiel $T_{\rm D} = T/10) $ wäre $\ddot{o}(T_{\rm D})$ etwas kleiner und damit die Fehlerwahrscheinlichkeit deutlich größer. Dieser Fall ist in der rechten Grafik durch die violett–gestrichelte Vertikale angedeutet.
Mittlere Fehlerwahrscheinlichkeit
Wir gehen wie bei den bisherigen Grafiken in diesem Kapitel von folgenden Voraussetzungen aus:
- NRZ–Rechtecke mit Amplitude $s_0$, AWGN–Rauschen mit $N_0$, wobei
- $$10 \cdot {\rm lg}\hspace{0.1cm} \frac{s_0^2 \cdot T}{N_0}\approx 13\,{\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{N_0}{s_0^2 \cdot T} = 0.05\hspace{0.05cm}.$$
- Gaußförmiges Empfangsfilter mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.4$:
- $$\sigma_d^2 = \frac{(N_0 /T)\cdot (f_{\rm G}\cdot T)}{\sqrt{2}}= \frac{0.05 \cdot s_0^2\cdot0.4}{\sqrt{2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma_d = \sqrt{0.0141}\cdot s_0 \approx 0.119 \cdot s_0 \hspace{0.05cm}.$$
- Es gelte $g_d(\nu \cdot T) \approx 0$ für $|\nu| \ge 2$. Die anderen Detektionsgrundimpulswerte sind wie folgt gegeben:
- $$g_0 = g_d(t=0) \approx 0.68 \cdot s_0, \hspace{0.5cm}g_1 = g_d(t=T) \approx 0.16 \cdot s_0, \hspace{0.2cm} g_{-1} = g_d(t=-T) \approx 0.16 \cdot s_0\hspace{0.05cm}.$$
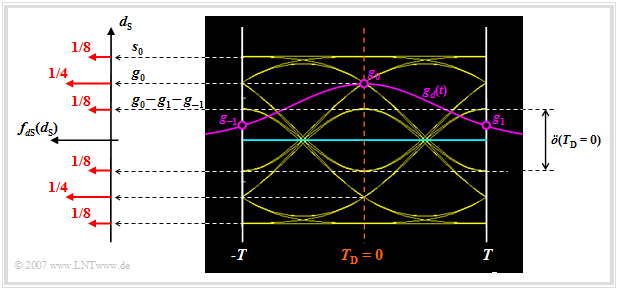
Analysieren wir nun die möglichen Werte für das Detektionsnutzsignal $d_{\rm S}(t)$ zu den Detektionszeitpunkten:
- Von den insgesamt $32$ Augenlinien schneiden vier Linien die Ordinate $(t = 0)$ bei $g_0 + 2 \cdot g_1 = s_0$. Diese Linien gehören zu den Amplitudenkoeffizienten "$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$". Kursiv hervorgehoben ist hierbei der "mittlere" Koeffizient $a_{\nu = 0}$.
- Die vier Augenlinien, die jeweils die Koeffizienten "$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} \text{...}$" repräsentieren, ergeben den Nutzabtastwert $d_{\rm S}(T_{\rm D} = 0) =g_0 - 2 \cdot g_1 = 0.36 \cdot s_0$.
- Dagegen tritt der Nutzabtastwert $d_{\rm S}(T_{\rm D} = 0) =g_0 = 0.68 \cdot s_0$ doppelt so häufig auf. Dieser geht entweder auf die Koeffizienten "$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$" oder auf "$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$" zurück.
- Für die $16$ Augenlinien, welche die Ordinate $T_{\rm D} = 0$ unterhalb der Entscheiderschwelle $E = 0$ schneiden, ergeben sich genau spiegelbildliche Verhältnisse.
Die möglichen Werte $d_{\rm S}(T_{\rm D})$ und deren Auftrittswahrscheinlichkeiten findet man in obiger Grafik auf der linken Seite in der Wahrscheinlichkeitsdichtefunktion (WDF) der Detektionsnutzabtastwerte wieder:
- $$f_{d{\rm S}}(d_{\rm S}) = {1}/{8} \cdot \delta (d_{\rm S} - s_0)+ {1}/{4} \cdot \delta (d_{\rm S} - 0.68 \cdot s_0)+ {1}/{8} \cdot \delta (d_{\rm S} - 0.36 \cdot s_0)+ $$
$$\hspace{2.15cm} + \hspace{0.2cm} {1}/{8} \cdot \delta (d_{\rm S} + s_0)+{1}/{4} \cdot \delta (d_{\rm S} + 0.68 \cdot s_0)+{1}/{8} \cdot \delta (d_{\rm S} + 0.36 \cdot s_0)\hspace{0.05cm}.$$
Damit kann die (mittlere) Symbolfehlerwahrscheinlichkeit des impulsinterferenzbehafteten Systems angegeben werden. Unter Ausnutzung der Symmetrie erhält man mit $\sigma_d/s_0 = 0.119$:
- $$p_{\rm S} = {1}/{4} \cdot {\rm Q} \left( \frac{s_0}{ \sigma_d} \right)+ {1}/{2} \cdot {\rm Q} \left( \frac{0.68 \cdot s_0}{ \sigma_d} \right)+{1}/{4} \cdot {\rm Q} \left( \frac{0.36 \cdot s_0}{ \sigma_d} \right)$$
- $$\Rightarrow \hspace{0.3cm}p_{\rm S} \approx {1}/{4} \cdot {\rm Q}(8.40) +{1}/{2} \cdot {\rm Q}(5.71)+ {1}/{4} \cdot {\rm Q}(3.02)\approx {1}/{4} \cdot 2.20 \cdot 10^{-17}+ {1}/{2} \cdot 1.65 \cdot 10^{-9}+ {1}/{4} \cdot 1.26 \cdot 10^{-3} \approx 3.14 \cdot 10^{-4} \hspace{0.05cm}.$$
$\text{Fazit:}$ Anhand dieses Zahlenbeispiels erkennt man:
- Bei Vorhandensein von Impulsinterferenzen wird die (mittlere) Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ im Wesentlichen durch die inneren Augenlinien bestimmt.
- Der Rechenaufwand zur Bestimmung der Fehlerwahrscheinlichkeit $p_{\rm S}$ kann sehr groß werden, insbesondere dann, wenn die Impulsinterferenzen von sehr vielen Grundimpulswerten $g_\nu$ herrühren.
$\text{Beispiel 4:}$
- Sind die Grundimpulswerte $g_{-5}, \text{...} \ , g_{+5}$ von Null verschieden und $E \ne 0$, so ist zur Bestimmung der Fehlerwahrscheinlichkeit $p_{\rm S}$ eine Mittelung über $2^{11} = 2048$ Augenlinien erforderlich.
- Sind dagegen nur die Grundimpulswerte $g_{-1}, \ g_0, \ g_{+1}$ von Null verschieden und wird zudem die Symmetrie bezüglich der Schwelle $E = 0$ berücksichtigt, so reduziert sich der Aufwand auf die Mittelung über vier Terme.
- Gilt zusätzlich die Symmetrie $g_{-1} = g_{+1}$ wie bei den obigen Zahlenwerten, so kann auch die Symmetrie bezüglich $T_{\rm D}$ ausgenutzt werden und es genügt die Mittelung über drei Terme.
Ungünstigste Fehlerwahrscheinlichkeit
In der Vergangenheit wurden eine Vielzahl von Näherungen für die mittlere Fehlerwahrscheinlichkeit angegeben, unter Anderem:
$\text{Definition:}$ Als eine sehr einfache Näherung für die tatsächliche Fehlerwahrscheinlichkeit $p_{\rm S}$ verwendet man häufig die ungünstigste Fehlerwahrscheinlichkeit (englisch: Worst-Case Error Probability)
- $$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} \right) \hspace{0.05cm}.$$
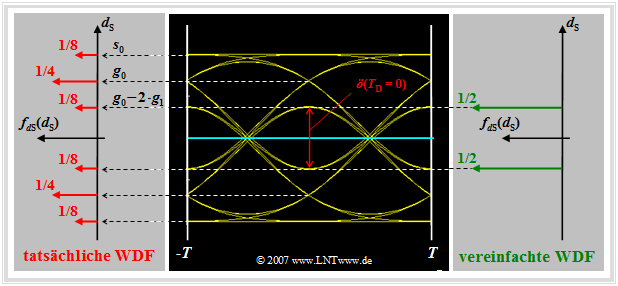
Für deren Berechnung wird stets von den ungünstigsten Symbolfolgen ausgegangen. Das bedeutet:
- Die tatsächliche WDF der Nutzabtastwerte (linke Grafik: sechs rote Diracs) wird durch eine vereinfachte WDF mit nur den inneren Diracfunktionen (rechte Grafik: zwei grüne Diracs) ersetzt.
- Für die halbe vertikale Augenöffnung gilt mit den Grundimpulswerten $g_\nu = g_d( T_{\rm D}+ \nu \cdot T)$ allgemein:
- $$\ddot{o}(T_{\rm D})/{ 2}= g_0 - \sum_{\nu = 1}^{n} \vert g_{\nu} \vert- \sum_{\nu = 1}^{v} \vert g_{-\nu} \vert \hspace{0.05cm}.$$
Diese Gleichung kann wie folgt interpretiert werden:
- $g_0 = g_d( T_{\rm D})$ ist der so genannte Hauptwert des Grundimpulses. Bei Nyquistsystemen gilt stets $\ddot{o}(T_{\rm D})/{ 2}= g_0$. Im Folgenden wird (meist) $T_{\rm D}= 0$ gesetzt.
- Die erste Summe beschreibt die Impulsinterferenzen der $n$ Nachläufer vorangegangener Impulse. Stillschweigend vorausgesetzt wird $g_\nu = 0$ für $\nu \gt n$.
- Die zweite Summe berücksichtigt den Einfluss der $v$ Vorläufer nachfolgender Impulse unter der Voraussetzung $g_{-\nu} = 0$ für $\nu \gt v$.
- Sind alle Impulsvor– und –nachläufer positiv, so lauten die beiden ungünstigsten Symbolfolgen "$\text{...}\hspace{0.05cm} -\hspace{-0.1cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}1,\hspace{0.05cm} -\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$" und "$\text{...}\hspace{0.05cm} +\hspace{-0.1cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} {\it -\hspace{-0.05cm}1},\hspace{0.05cm} +\hspace{-0.05cm}1,\hspace{0.05cm} +\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$" (der Koeffizient $a_{\nu = 0}$ ist jeweils kursiv). Diese Angaben treffen zum Beispiel für das hier betrachtete gaußförmige Empfangsfilter zu.
- Sind einige Grundimpulswerte negativ, so wird dies in obiger Gleichung durch die Betragsbildung berücksichtigt. Es ergeben sich dann andere "Worst–Case"–Folgen als gerade genannt.
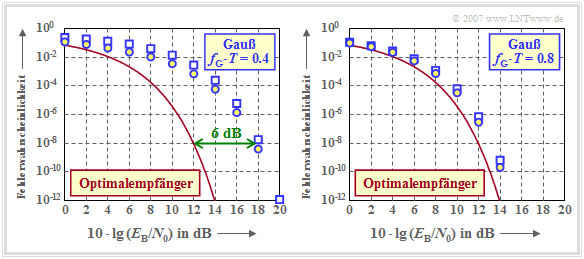
$\text{Beispiel 5:}$ Die Grafik zeigt die Fehlerwahrscheinlichkeiten des AWGN–Kanals in Abhängigkeit des (logarithmierten) Quotienten $E_{\rm B}/N_0$, nämlich
- die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ bei gaußförmigem Empfangsfilter (blaue Kreise),
- die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ bei gaußförmigem Empfangsfilter (blaue Rechtecke),
- die kleinstmögliche Fehlerwahrscheinlichkeit gemäß der Seite Optimaler Binärempfänger (rote Kurve).
Die Energie pro Bit ist dabei gleich $E_{\rm B} = s_0^2 \cdot T$ (NRZ–Rechteck–Sendeimpulse).
Die linke Grafik gilt für die (normierte) Grenzfrequenz $f_{\rm G} \cdot T = 0.4$, die rechte für ein breitbandigeres Empfangsfilter mit $f_{\rm G} \cdot T = 0.8$. Die Ergebnisse können wie folgt interpretiert werden:
- Die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ ist stets eine obere Schranke für die tatsächliche Symbolfehlerwahrscheinlichkeit $p_{\rm S}$. Je kleiner der Einfluss der Impulsinterferenzen ist (große Grenzfrequenz), um so näher liegen $p_{\rm S}$ und $p_{\rm U}$ zusammen. Beim Optimalempfänger gilt $p_{\rm S} = p_{\rm U}.$
- Bei gaußförmigem Empfangsfilter mit $f_{\rm G} \cdot T \ge 0.3$ werden die Impulsinterferenzen allein durch die Nachbarimpulse hervorgerufen $(g_2 = g_3 = \text{...} \approx 0)$, so dass für $p_{\rm S}$ auch eine untere Schranke angegeben werden kann:
- $${p_{\rm U} }/{ 4} \le p_{\rm S} \le p_{\rm U} \hspace{0.05cm}.$$
- Die starken Impulsinterferenzen eines gaußförmigen Empfangsfilters mit $f_{\rm G} \cdot T = 0.4$ führen dazu, dass gegenüber dem Optimalempfänger ein um $6 \ \rm dB$ größeres $E_{\rm B}/N_0$ aufgewendet werden muss (vierfache Leistung), damit die Fehlerwahrscheinlichkeit den Wert $10^{-8}$ nicht überschreitet.
- Der horizontale Abstand zwischen der blauen $p_{\rm S}$–Kurve (markiert durch Kreise) und der roten Vergleichskurve ist aber nicht konstant. Bei $p_{\rm S} = 10^{-2}$ beträgt der Abstand nur $4 \ \rm dB$.
- Die rechte Grafik zeigt, dass mit $f_{\rm G} \cdot T = 0.8$ der Abstand zum Vergleichssystem weniger als $1 \ \rm dB$ beträgt. Auf der nächsten Seite wird gezeigt, dass bei einem gaußförmigen Empfangsfilter die (normierte) Grenzfrequenz $f_{\rm G} \cdot T \approx 0.8$ das Optimum darstellt.
Optimierung der Grenzfrequenz
Für die Systemoptimierung und den Systemvergleich erweist es sich als zweckmäßig,
- anstelle der ungünstigsten Fehlerwahrscheinlichkeit $p_{\rm U}$
- das ungünstigste Signal–zu–Rausch–Leistungsverhältnis (S/N-Verhältnis) zu verwenden:
- $$\rho_{\rm U} = [\ddot{o}(T_{\rm D})]^2/ \sigma_d^2.$$
Bei Gaußscher Störung besteht folgender Zusammenhang:
- $$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right) \hspace{0.05cm}.$$
Die mittlere Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ kann formal über die Q–Funktion ebenfalls durch ein S/N–Verhältnis ausgedrückt werden:
- $$\rho_d = \left[{\rm Q}^{-1} \left( p_{\rm S} \right)\right]^2 \hspace{0.05cm}.$$
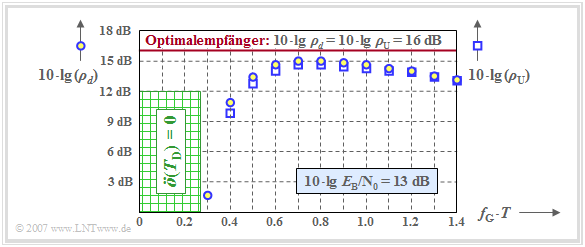
Die Grafik zeigt die beiden Größen $\rho_d$ und $\rho_{\rm U}$ in logarithmischer Form abhängig von der normierten Grenzfrequenz $f_{\rm G} \cdot T$ eines gaußförmigen Empfangsfilters, wobei $10 \cdot {\rm lg}\hspace{0.1cm} E_{\rm B}/N_0 = 13 \ \rm dB$ zugrunde liegt.
- Die blau umrandeten Kreise gelten für $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d$ ⇒ "mittleres" Detektions–SNR,
- Die blau umrandeten Quadrate markieren $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U}$ ⇒ "ungünstigstes" SNR.
Zum Vergleich ist als rote horizontale Linie auch das Ergebnis für den optimalen Binärempfänger eingezeichnet. Für diesen gilt:
- $$\rho_d = \rho_{\rm U} = {2 \cdot E_{\rm B}}/{ N_0}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm} \rho_d = 10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx 16\,{\rm dB} \hspace{0.05cm}.$$
Man erkennt aus der Darstellung:
- Das Optimierungskriterium $\rho_d$ führt zur optimalen Grenzfrequenz $f_\text{G, opt} \cdot T = 0.8$. Eine kleinere Grenzfrequenz hat stärkere Impulsinterferenzen zur Folge (kleinere Augenöffnung), eine größere Grenzfrequenz bewirkt einen größeren Rauscheffektivwert $\sigma_d$.
- Ein solches gaußförmiges Empfangsfilter mit $f_\text{G, opt} \cdot T \approx 0.8$ führt zum Störabstand $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 15 \ \rm dB$ und damit zur Fehlerwahrscheinlichkeit $p_{\rm S} \approx 10^{-8}$. Zum Vergleich: Für den optimalen Empfänger (an den Sender angepasste Impulsantwort) ergeben sich $10 \cdot {\rm lg}\hspace{0.1cm} \rho_d \approx 16 \ \rm dB$ und $p_{\rm S} \approx 10^{-10}$.
- Die Grafik zeigt aber auch, dass das sehr viel einfachere Optimierungskriterien $ \rho_{\rm U}$ $($bzw. $ p_{\rm U})$ näherungsweise zur gleichen optimalen Grenzfrequenz $f_\text{G, opt} \cdot T = 0.8$ führt. Für diese Grenzfrequenz erhält man $10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U} \approx 14.7 \ \rm dB$ sowie die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} \approx 3 \cdot 10^{-8}$.
- Ist die Grenzfrequenz $f_\text{G} \cdot T < 0.27$, so ergibt sich für die vertikale Augenöffnung immer $\ddot{o}(T_{\rm D}) = 0$. Man spricht von einem geschlossenen Auge. Dies hat zur Folge, dass einige ungünstige Impulsfolgen auch ohne Rauschen immer falsch entschieden würden. Es tritt ein systematischer Fehler auf.
- Weitere Untersuchungen haben gezeigt, dass das Optimierungskriterium $ \rho_{\rm U}$ auch bei kleinerem $E_{\rm B}/N_0$ ausreichend ist. Bei einem verzerrungsfreien Kanal ⇒ $H_{\rm K}(f) = 1$, ergibt sich somit die optimale Grenzfrequenz des Gaußtiefpasses stets zu $f_\text{G, opt} \cdot T \approx 0.8$, zumindest bei realitätsnaher Betrachtungsweise.
Alle Aussagen dieses Kapitels können mit dem interaktiven Applet Augendiagramm und Augenöffnung nachvollzogen werden.
Aufgaben zum Kapitel
Aufgabe 3.2: Augendiagramm nach Gaußtiefpass
Aufgabe 3.2Z: Optimale Grenzfrequenz bei Gauß-Tiefpass