Exercise 2.6Z: PN Generator of Length 3
From LNTwww
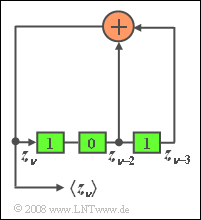
- Nebenstehende Skizze zeigt einen PN-Generator der Länge $L = 3$ mit dem Generatorpolynom
- $$G(\it D) = \it D^{\rm 3} + \it D^{\rm 2} + \rm 1$$
- und somit der Oktalkennung ($g_3 g_2 g_1 g_0$) = $(1101)_{bin} = (15)_{oct}$. Das zugehörige reziproke Polynom
- $$G_{\rm R}(\it D) = \it D^{\rm 3} (\it D^{\rm -3} + \it D^{\rm -2} + \rm 1) =\it D^{\rm 3} + \it D^{\rm 1} + \rm 1$$
- hat die Oktalkennung $(1011)_{bin} = (13)_{oct}$.
- Beide Anordnungen erzeugen eine M-Sequenz. Zum Startzeitpunkt seien die drei Speicherzellen mit den Binärwerten 1, 0 und 1 vorbelegt.
- Hinweis: Die Aufgabe bezieht sich auf Lehrstoff von Kapitel 2.5. Wir möchten Sie gerne auch auf das folgende Lernvideo hinweisen:
Fragebogen
Musterlösung
- 1. Es handelt sich um eine M-Sequenz mit L = 3. Daraus folgt P = 2L - 1 = 7.
- 2. Wir bezeichnen die Zellen von links nach rechts mit S1, S2 und S3. Dann gilt:
- S2(ν) = S1(ν – 1),
- S3(ν) = S2(ν – 1),
- S3(ν) = S2(ν – 1) mod S3(ν – 1).
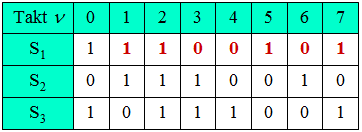
- Das Ergebnis ist in der ersten Zeile obiger Tabelle (rot markiert) eingetragen:
- Zum Taktzeitpunkt ν = 7 ergibt sich die gleiche Speicherbelegung wie zum Zeitpunkt ν = 0. Daraus folgt P = 7 und die Folge ist ab ν = 1: 〈zν〉 = 〈 1 1 0 0 1 0 1 1 1 0 0 1 0 1 1 ... 〉.
- Vorschlag 3 ist der richtige. Vorschlag 1 beschreibt die M-Sequenz des PN-Generators mit Länge L = 4 und Kennung (31); die Periodenlänge ist P = 15. Beim Vorschlag 2 ist P = 4.
- Der letzte Vorschlag schließlich hätte zwar die gewünschte Periodenlänge P = 7, aber aus der Modulo-2-Addition von S2 = 0 und S3 = 1 (für ν = 0) folgt zum nächsten Zeitpunkt (ν = 1) zwingend: S1 = 1. Diese Eigenschaft zeigt die Folge 4 nicht.
- 3. Die maximale Anzahl aufeinander folgender Einsen ist L (nämlich dann, wenn in allen L Speicherzellen eine Eins steht). Es ist dagegen nicht möglich, dass alle Speicherzellen mit Nullen belegt sind. Deshalb gibt es stets eine Eins mehr als Nullen.
- Die Periodenlänge der letzten Folge beträgt P = 2. Bei einer M-Sequenz gilt dagegen P = 2L – 1. Für keinen Wert von L ist P = 2 möglich.
- Richtig sind somit die Lösungsvorschläge 2, 3 und 4.
- 4. Auch bei der reziproken Anordnung muss die Periodenlänge P = 7 gelten, so dass der Vorschlag 1 (mit P = 15) ausscheidet. Der Vorschlag 3 ist nur eine um 2 Zeittakte verschobene Version der Ausgangsfolge von (15). Dagegen ist im zweiten Vorschlag die Inverse von .... 1 1 0 0 1 0 1 ... – also die Folge ... 1 0 1 0 0 1 1 ... – enthalten, wenn auch mit einem Phasenversatz.
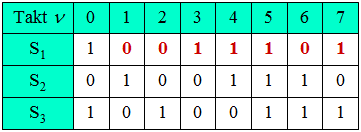
- In der unteren Tabelle ist die Entstehung der PN–Folge beim reziproken Polynom GR(D) eingetragen. Die Tabelle bestätigt die Richtigkeit von Lösungsvorschlag 2.