Difference between revisions of "Information Theory/AWGN Channel Capacity for Discrete-Valued Input"
| Line 12: | Line 12: | ||
[[File:P_ID2931__Inf_T_4_3_S1a.png|center|frame|Two largely equivalent models for the AWGN channel]] | [[File:P_ID2931__Inf_T_4_3_S1a.png|center|frame|Two largely equivalent models for the AWGN channel]] | ||
| − | + | The maximum mutual information $I(X; Y)$ between input and output ⇒ channel capacity $C$ is obtained when there is a Gaussian input PDF $f_X(x)$ vorliegt. With the transmit power $P_X = σ_X^2$ ⇒ variance of the random variable $X$ , the channel capacity equation is: | |
:$$C = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + {P_X}/{P_N}) | :$$C = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + {P_X}/{P_N}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Now we describe the AWGN channel model according to the case sketched on the right, where the sequence $〈X_ν〉$ is applied to the channel input, where the distance between successive values is $T_{\rm A}$ . This sequence is the discrete-time equivalent of the continuous-time signal $X(t)$ after band limiting and sampling. | |
| − | + | The relationship between the two models can be established by means of a graph, which is described in more detail below. | |
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= The $\text{important insights}$ : |
| − | * | + | *In the right-hand model, the same relationship $Y_ν = X_ν + N_ν$ applies at the sampling times $ν·T_{\rm A}$ as in the left-hand model. |
| − | * | + | *The noise component $N_ν$ is now to be modelled by band-limited $($auf $±B)$ white noise with the two-sided power density ${\it Φ}_N(f) = N_0/2$ , where $B = 1/(2T_{\rm A})$ must hold ⇒ see [[Signal_Representation/Time_Discrete_Signal_Representation#The_Sampling_Theorem|sampling theorem]].}} |
$\text{ Interpretation:}$ | $\text{ Interpretation:}$ | ||
| − | + | In the modified model, we assume an infinite sequence $〈X_ν〉$ of Gaussian random variables impressed on a [[Signal_Representation/Time_Discrete_Signal_Representation#Time_Domain_Representation|Diracpuls]] $p_δ(t)$ . The resulting discrete-time signal is thus: | |
:$$X_{\delta}(t) = T_{\rm A} \cdot \hspace{-0.1cm} \sum_{\nu = - \infty }^{+\infty} X_{\nu} \cdot | :$$X_{\delta}(t) = T_{\rm A} \cdot \hspace{-0.1cm} \sum_{\nu = - \infty }^{+\infty} X_{\nu} \cdot | ||
| Line 34: | Line 34: | ||
)\hspace{0.05cm}.$$ | )\hspace{0.05cm}.$$ | ||
| − | + | The spacing of all (weighted) Dirac functions is uniform $T_{\rm A}$. | |
| − | [[File:P_ID2932__Inf_T_4_3_S1b.png|center|frame| | + | [[File:P_ID2932__Inf_T_4_3_S1b.png|center|frame| AWGN model considering time discretisation and band limitation]] |
| − | + | Through the interpolation filter with the impulse response $h(t)$ as well as the frequency response $H(f)$, where | |
:$$h(t) = 1/T_{\rm A} \cdot {\rm si}(\pi \cdot t/T_{\rm A}) \quad \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad H(f) = | :$$h(t) = 1/T_{\rm A} \cdot {\rm si}(\pi \cdot t/T_{\rm A}) \quad \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad H(f) = | ||
| Line 44: | Line 44: | ||
\hspace{0.5cm} B = \frac{1}{T_{\rm A}}$$ | \hspace{0.5cm} B = \frac{1}{T_{\rm A}}$$ | ||
| − | + | must hold, the continuous-time signal $X(t)$ is obtained with the following properties: | |
| − | * | + | *The samples $X(ν·T_{\rm A})$ are identical to the input values $X_ν$ for all integers $ν$ , which can be justified by the equidistant zeros of the [[Signal_Representation/Special_Cases_of_Impulse_Signals#Rechteckimpuls|sinc - function]] ⇒ $\text{si}(x) = \sin(x)/x$ . |
| − | * | + | *According to the sampling theorem, $X(t)$ is ideally bandlimited to the spectral range $±B$ , as the above calculation has shown ⇒ rectangular frequency response $H(f)$ of the one-sided bandwidth $B$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Noise power:}$ After adding the noise $N(t)$ with the (two-sided) power density ${\it Φ}_N(t) = N_0/2$ , the matched filter $\rm (MF)$ with sinc–shaped impulse response follows. The following then applies to the '''noise power at the MF output''' : |
:$$P_N = {\rm E}\big[N_\nu^2 \big] = \frac{N_0}{2T_{\rm A} } = N_0 \cdot B\hspace{0.05cm}.$$}} | :$$P_N = {\rm E}\big[N_\nu^2 \big] = \frac{N_0}{2T_{\rm A} } = N_0 \cdot B\hspace{0.05cm}.$$}} | ||
| Line 56: | Line 56: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Proof:}$ |
| − | + | With $B = 1/(2T_{\rm A} )$ one obtains for the impulse response $h_{\rm E}(t)$ and the spectral function $H_{\rm E}(f)$: | |
:$$h_{\rm E}(t) = 2B \cdot {\rm si}(2\pi \cdot B \cdot t) \quad \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad H_{\rm E}(f) = | :$$h_{\rm E}(t) = 2B \cdot {\rm si}(2\pi \cdot B \cdot t) \quad \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad H_{\rm E}(f) = | ||
| Line 64: | Line 64: | ||
$$ | $$ | ||
| − | + | It follows, according to the insights of [[Theory_of_Stochastic_Signals/Stochastische_Systemtheorie#Problemstellung|theory of stochastic signals]]: | |
:$$P_N = | :$$P_N = | ||
| Line 75: | Line 75: | ||
| − | + | Further: | |
| − | * | + | *If one samples the matched–filter output signal at equidistant intervals $T_{\rm A}$ , the same constellation as before results for the time instants $ν ·T_{\rm A}$ , namely: $Y_ν = X_ν + N_ν$. |
| − | * | + | *The noise component $N_ν$ in the discrete-time output signal $Y_ν$ is thus „band limited” and „white”. The channel capacity equation thus needs to be adjusted only slightly. |
| − | * | + | *With $\text{energy per symbol}$ $E_{\rm S} = P_X \cdot T_{\rm A}$ ⇒ transmission energy within a „symbol duration” $T_{\rm A}$ then holds: |
:$$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac {P_X}{N_0 \cdot B}) | :$$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac {P_X}{N_0 \cdot B}) | ||
Revision as of 19:53, 19 April 2021
Contents
- 1 AWGN model for discrete-time band-limited signals
- 2 Die Kanalkapazität $C$ als Funktion von $E_{\rm S}/N_0$
- 3 Systemmodell zur Interpretation der AWGN–Kanalkapazität
- 4 Die Kanalkapazität $C$ als Funktion von $E_{\rm B}/N_0$
- 5 AWGN–Kanalkapazität für binäre Eingangssignale
- 6 Vergleich zwischen Theorie und Praxis
- 7 Kanalkapazität des komplexen AWGN–Kanals
- 8 Maximale Coderate für QAM–Strukturen
- 9 Aufgaben zum Kapitel
- 10 Quellenverzeichnis
AWGN model for discrete-time band-limited signals
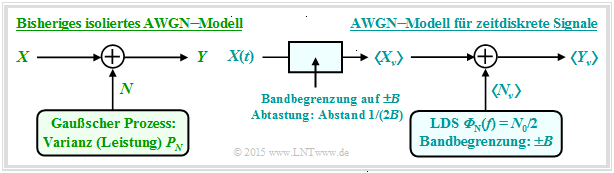
At the end of the last chapter , the AWGN model was used according to the left graph, characterised by the two random variables $X$ and $Y$ at the input and output and the stochastic noise $N$ as the result of a mean-free Gaussian random process ⇒ „White noise” with variance $σ_N^2$. The interference power $P_N$ is also equal toh $σ_N^2$.
The maximum mutual information $I(X; Y)$ between input and output ⇒ channel capacity $C$ is obtained when there is a Gaussian input PDF $f_X(x)$ vorliegt. With the transmit power $P_X = σ_X^2$ ⇒ variance of the random variable $X$ , the channel capacity equation is:
- $$C = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + {P_X}/{P_N}) \hspace{0.05cm}.$$
Now we describe the AWGN channel model according to the case sketched on the right, where the sequence $〈X_ν〉$ is applied to the channel input, where the distance between successive values is $T_{\rm A}$ . This sequence is the discrete-time equivalent of the continuous-time signal $X(t)$ after band limiting and sampling.
The relationship between the two models can be established by means of a graph, which is described in more detail below.
The $\text{important insights}$ :
- In the right-hand model, the same relationship $Y_ν = X_ν + N_ν$ applies at the sampling times $ν·T_{\rm A}$ as in the left-hand model.
- The noise component $N_ν$ is now to be modelled by band-limited $($auf $±B)$ white noise with the two-sided power density ${\it Φ}_N(f) = N_0/2$ , where $B = 1/(2T_{\rm A})$ must hold ⇒ see sampling theorem.
$\text{ Interpretation:}$
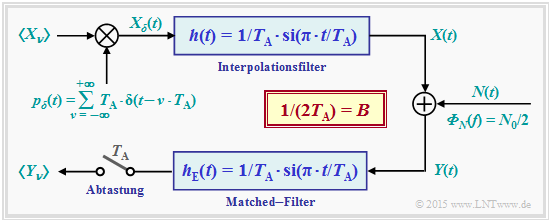
In the modified model, we assume an infinite sequence $〈X_ν〉$ of Gaussian random variables impressed on a Diracpuls $p_δ(t)$ . The resulting discrete-time signal is thus:
- $$X_{\delta}(t) = T_{\rm A} \cdot \hspace{-0.1cm} \sum_{\nu = - \infty }^{+\infty} X_{\nu} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
The spacing of all (weighted) Dirac functions is uniform $T_{\rm A}$.
Through the interpolation filter with the impulse response $h(t)$ as well as the frequency response $H(f)$, where
- $$h(t) = 1/T_{\rm A} \cdot {\rm si}(\pi \cdot t/T_{\rm A}) \quad \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad H(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B, \\ {\rm{f\ddot{u}r}} \hspace{0.3cm} |f| > B, \\ \end{array} \hspace{0.5cm} B = \frac{1}{T_{\rm A}}$$
must hold, the continuous-time signal $X(t)$ is obtained with the following properties:
- The samples $X(ν·T_{\rm A})$ are identical to the input values $X_ν$ for all integers $ν$ , which can be justified by the equidistant zeros of the sinc - function ⇒ $\text{si}(x) = \sin(x)/x$ .
- According to the sampling theorem, $X(t)$ is ideally bandlimited to the spectral range $±B$ , as the above calculation has shown ⇒ rectangular frequency response $H(f)$ of the one-sided bandwidth $B$.
$\text{Noise power:}$ After adding the noise $N(t)$ with the (two-sided) power density ${\it Φ}_N(t) = N_0/2$ , the matched filter $\rm (MF)$ with sinc–shaped impulse response follows. The following then applies to the noise power at the MF output :
- $$P_N = {\rm E}\big[N_\nu^2 \big] = \frac{N_0}{2T_{\rm A} } = N_0 \cdot B\hspace{0.05cm}.$$
$\text{Proof:}$ With $B = 1/(2T_{\rm A} )$ one obtains for the impulse response $h_{\rm E}(t)$ and the spectral function $H_{\rm E}(f)$:
- $$h_{\rm E}(t) = 2B \cdot {\rm si}(2\pi \cdot B \cdot t) \quad \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad H_{\rm E}(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} \text{für} \hspace{0.3cm} \vert f \vert \le B, \\ \text{für} \hspace{0.3cm} \vert f \vert > B. \\ \end{array} $$
It follows, according to the insights of theory of stochastic signals:
- $$P_N = \int_{-\infty}^{+\infty} \hspace{-0.3cm} {\it \Phi}_N (f) \cdot \vert H_{\rm E}(f)\vert^2 \hspace{0.15cm}{\rm d}f = \int_{-B}^{+B} \hspace{-0.3cm} {\it \Phi}_N (f) \hspace{0.15cm}{\rm d}f = \frac{N_0}{2} \cdot 2B = N_0 \cdot B \hspace{0.05cm}.$$
Further:
- If one samples the matched–filter output signal at equidistant intervals $T_{\rm A}$ , the same constellation as before results for the time instants $ν ·T_{\rm A}$ , namely: $Y_ν = X_ν + N_ν$.
- The noise component $N_ν$ in the discrete-time output signal $Y_ν$ is thus „band limited” and „white”. The channel capacity equation thus needs to be adjusted only slightly.
- With $\text{energy per symbol}$ $E_{\rm S} = P_X \cdot T_{\rm A}$ ⇒ transmission energy within a „symbol duration” $T_{\rm A}$ then holds:
- $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac {P_X}{N_0 \cdot B}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac {2 \cdot P_X \cdot T_{\rm A}}{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac {2 \cdot E_{\rm S}}{N_0}) \hspace{0.05cm}.$$
Die Kanalkapazität $C$ als Funktion von $E_{\rm S}/N_0$
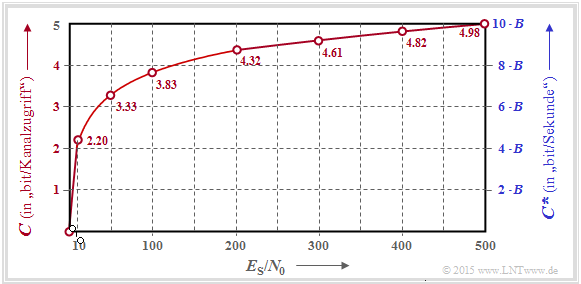
$\text{Beispiel 1:}$ Die Grafik zeigt den Verlauf der AWGN–Kanalkapazität in Abhängigkeit des Quotienten $E_{\rm S}/N_0$, wobei die linke Koordinatenachse und die roten Beschriftungen gültig sind:
- $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S} }{N_0}) \hspace{0.5cm}{\rm Einheit\hspace{-0.15cm}: \hspace{0.05cm}bit/Kanalzugriff\hspace{0.15cm} (englisch\hspace{-0.15cm}: \hspace{0.05cm}bit/channel\hspace{0.15cm}use)} \hspace{0.05cm}.$$
Die (Pseudo–)Einheit wird manchmal auch mit „bit/Quellensymbol” oder kurz „bit/Symbol” bezeichnet.
Die rechte (blaue) Achsenbeschriftung berücksichtigt die Beziehung $B = 1/(2T_{\rm A})$ und liefert somit eine obere Schranke für die Bitrate $R$ eines Digitalsystems, die bei diesem AWGN–Kanal noch möglich ist.
- $$C^{\hspace{0.05cm}*} = \frac{C}{T_{\rm A} } = B \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S} }{N_0}) \hspace{1.0cm}{\rm Einheit\hspace{-0.15cm}: \hspace{0.05cm}bit/Sekunde} \hspace{0.05cm}.$$
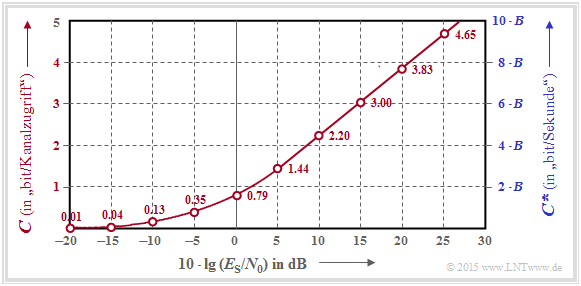
$\text{Beispiel 2:}$ Oft gibt man den Quotienten aus Symbolenergie $(E_{\rm S})$ und AWGN–Rauschleistungsdichte $(N_0)$ logarithmisch an.
- Diese Grafik zeigt die Kanalkapazitäten $C$ bzw. $C^{\hspace{0.05cm}*}$ als Funktion von $10 · \lg (E_{\rm S}/N_0)$ im Bereich von $-20 \ \rm dB$ bis $+30 \ \rm dB$.
- Ab etwa $10 \ \rm dB$ ergibt sich hier ein (nahezu) linearer Verlauf.
Systemmodell zur Interpretation der AWGN–Kanalkapazität
Um das Kanalcodierungstheorem im Zusammenhang mit dem AWGN–Kanal besprechen zu können, benötigen wir noch eine „Codiervorrichtung”, die hier allerdings informationstheoretisch allein durch die Coderate $R$ gekennzeichnet wird.
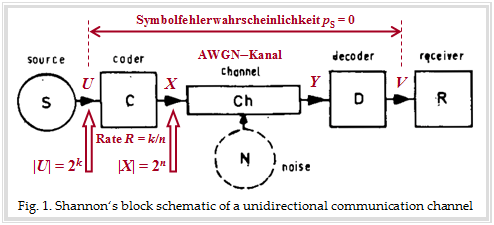
Die Grafik beschreibt das von Shannon betrachtete Nachrichtensystem mit den Blöcken Quelle, Coder, (AWGN–)Kanal, Decoder und Empfänger. Im Hintergrund erkennt man ein Originalbild aus einem Aufsatz über die Shannon–Theorie. Rot eingezeichnet wurden von uns einige Bezeichnungen und Erläuterungen für den folgenden Text:
- Das Quellensymbol $U$ entstammt einem Alphabet mit $M_U = |U| = 2^k$ Symbolen und kann durch $k$ gleichwahrscheinliche statistisch unabhängige Binärsymbole repräsentiert werden.
- Das Alphabet des Codesymbols $X$ hat den Symbolumfang $M_X = |X| = 2^n$, wobei sich $n$ aus der Coderate $R = k/n$ ergibt.
- Für die Coderate $R = 1$ gilt somit $n = k$ und der Fall $n > k$ führt zu einer Coderate $R < 1$.
$\rm Kanalcodierungstheorem$
Dieses besagt, dass es (mindestens) einen Code der Rate $R$ gibt, der zur Symbolfehlerwahrscheinlichkeit $p_{\rm S} = \text{Pr}(V ≠ U) \equiv 0$ führt, falls folgende Bedingungen erfüllt sind:
- Die Coderate $R$ ist nicht größer als die Kanalkapazität $C$.
- Ein solcher geeigneter Code ist unendlich lang: $n → ∞$. Deshalb ist auch tatsächlich eine Gaußverteilung $f_X(x)$ am Kanaleingang möglich, die der bisherigen Berechnung der AWGN–Kanalkapazität stets zugrunde gelegt wurde:
- $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S} }{N_0}) \hspace{0.5cm}{\rm Einheit\hspace{-0.15cm}: \hspace{0.05cm}bit/Kanalzugriff\hspace{0.15cm} (englisch\hspace{-0.15cm}: \hspace{0.05cm}bit/channel \hspace{0.15cm}use)} \hspace{0.05cm}.$$
- Die Kanaleingangsgröße $X$ ist also wertkontinuierlich. Gleiches gilt für $U$ und für die Größen $Y$, $V$ nach dem AWGN–Kanal.
- Für einen Systemvergleich ist die Energie pro Symbol $(E_{\rm S} )$ allerdings ungeeignet. Ein Vergleich sollte vielmehr auf der Energie $E_{\rm B}$ pro Informationsbit ⇒ kurz: $\text{Energie pro Bit}$ basieren. Mit $E_{\rm B} = E_{\rm S}/R$ gilt somit auch:
- $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B} }{N_0}) \hspace{0.2cm}{\rm Einheit\hspace{-0.15cm}: \hspace{0.05cm}bit/Kanalzugriff\hspace{0.1cm} (englisch\hspace{-0.15cm}: \hspace{0.05cm}bit/channel \hspace{0.15cm}use)} \hspace{0.05cm}.$$
Diese beiden Gleichungen werden auf der nächsten Seite diskutiert.
Die Kanalkapazität $C$ als Funktion von $E_{\rm B}/N_0$
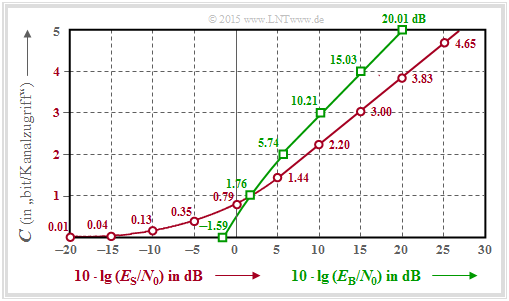
$\text{Beispiel 3:}$ Die Grafik zu diesem Beispiel zeigt die AWGN–Kanalkapazität $C$ als Funktion
- von $10 · \lg (E_{\rm S}/N_0)$ ⇒ roter Kurvenverlauf:
- $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S} }{N_0}) \hspace{1.5cm}{\rm Einheit\hspace{-0.15cm}: \hspace{0.05cm}bit/Kanalzugriff\hspace{0.15cm} (oder\hspace{-0.15cm}: \hspace{0.05cm}bit/Symbol)} \hspace{0.05cm}.$$
$\text{Rote Zahlen:}$ Kapazität $C$ in „$\rm bit/Symbol$” für $10 · \lg (E_{\rm S}/N_0) = -20 \ \rm dB, -15 \ \rm dB$, ... , $+30\ \rm dB$.
- von $10 · \lg (E_{\rm B}/N_0)$ ⇒ grüner Kurvenverlauf:
- $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B} }{N_0}) \hspace{1.2cm}{\rm Einheit\hspace{-0.15cm}: \hspace{0.05cm}bit/Kanalzugriff\hspace{0.1cm} (oder \hspace{-0.15cm}: \hspace{0.05cm}bit/Symbol)} \hspace{0.05cm}.$$
$\text{Grüne Zahlen:}$ Erforderliches $10 · \lg (E_{\rm B}/N_0)$ in „$\rm dB$” für $C = 0,\ 1$, ... , $5$ in „$\rm bit/Symbol$”.
Die ausführliche $C(E_{\rm B}/N_0)$–Berechnung finden Sie in der Aufgabe 4.8 und der zugehörigen Musterlösung.
Im Folgenden interpretieren wir das (grüne) $C(E_{\rm B}/N_0)$–Ergebnis im Vergleich zur (roten) $C(E_{\rm S}/N_0)$–Kurve:
- Wegen $E_{\rm S} = R · E_{\rm B}$ liegt der Schnittpunkt beider Kurven bei $C (= R) = 1$ (bit/Symbol). Erforderlich sind $10 · \lg (E_{\rm S}/N_0) = 1.76\ \rm dB$ bzw. $10 · \lg (E_{\rm B}/N_0) = 1.76\ \rm dB$ gleichermaßen.
- Im Bereich $C > 1$ liegt die grüne Kurve stets über der roten. Beispielsweise ergibt sich für $10 · \lg (E_{\rm B}/N_0) = 20\ \rm dB$ die Kanalkapazität $C ≈ 5$, für $10 · \lg (E_{\rm S}/N_0) = 20\ \rm dB$ nur $C = 3.83$.
- Ein Vergleich in horizontaler Richtung zeigt, dass die Kanalkapazität $C = 3$ bit/Symbol schon mit $10 · \lg (E_{\rm B}/N_0) \approx 10\ \rm dB$ erreichbar ist, man aber $10 · \lg (E_{\rm S}/N_0) \approx 15\ \rm dB$ benötigt.
- Im Bereich $C < 1$ liegt die rote Kurve stets über der grünen. Für jedes $E_{\rm S}/N_0 > 0$ gilt $C > 0$. Bei logarithmischer Abszisse wie in der vorliegenden Darstellung reicht somit die rote Kurve bis ins „Minus–Unendliche”.
- Dagegen endet die grüne Kurve bei $E_{\rm B}/N_0 = \ln (2) = 0.693$ ⇒ $10 · \lg (E_{\rm B}/N_0)= -1.59 \rm dB$ ⇒ absolute Grenze für die (fehlerfreie) Übertragung über den AWGN–Kanal.
AWGN–Kanalkapazität für binäre Eingangssignale
Auf den bisherigen Seiten dieses Kapitels wurde stets gemäß der Shannon–Theorie von einem gaußverteilten, also wertkontinuierlichen AWGN–Eingang $X$ ausgegangen. Nun betrachten wir den binären Fall und werden somit erst jetzt der Kapitel–Überschrift „AWGN–Kanalkapazität bei wertdiskretem Eingang” gerecht.
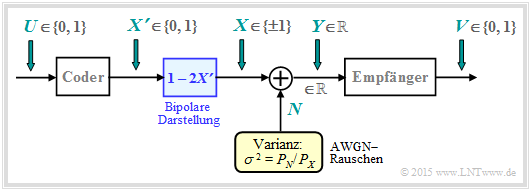
Die Grafik zeigt das zugrundeliegende Blockschaltbild für Binary Phase Shift Keying (BPSK) mit binärem Eingang $U$ und binärem Ausgang $V$. Durch die bestmögliche Codierung soll erreicht werden, dass die Fehlerwahrscheinlichkeit $\text{Pr}(V ≠ U)$ verschwindend klein wird.
- Der Coderausgang ist gekennzeichnet durch die binäre Zufallsgröße $X \hspace{0.03cm}' = \{0, 1\}$ ⇒ $M_{X'} = 2$, während der Ausgang $Y$ des AWGN–Kanals weiterhin wertkontinuierlich ist: $M_Y → ∞$.
- Durch das Mapping $X = 1 - 2X\hspace{0.03cm} '$ kommt man von der unipolaren Darstellung zu der für BPSK besser geeigneten bipolaren (antipodalen) Beschreibung: $X\hspace{0.03cm} ' = 0 → \ X = +1; \hspace{0.5cm} X\hspace{0.03cm} ' = 1 → X = -1$.
- Der AWGN–Kanal wird durch zwei bedingte Wahrscheinlichkeitsdichtefunktionen charakterisiert:
- $$f_{Y\hspace{0.05cm}|\hspace{0.03cm}{X}}(y\hspace{0.05cm}|\hspace{0.03cm}{X}=+1) =\frac{1}{\sqrt{2\pi\sigma^2}} \cdot {\rm exp}\left [-\frac{(y - 1)^2} { 2 \sigma^2})\right ] \hspace{0.05cm}\hspace{0.05cm},\hspace{0.5cm}\text{Kurzform:} \ \ f_{Y\hspace{0.05cm}|\hspace{0.03cm}{X}}(y\hspace{0.05cm}|\hspace{0.03cm}+1)\hspace{0.05cm},$$
- $$f_{Y\hspace{0.05cm}|\hspace{0.03cm}{X}}(y\hspace{0.05cm}|\hspace{0.03cm}{X}=-1) =\frac{1}{\sqrt{2\pi\sigma^2}} \cdot {\rm exp}\left [-\frac{(y + 1)^2} { 2 \sigma^2})\right ] \hspace{0.05cm}\hspace{0.05cm},\hspace{0.5cm}\text{Kurzform:} \ \ f_{Y\hspace{0.05cm}|\hspace{0.03cm}{X}}(y\hspace{0.05cm}|\hspace{0.03cm}-1)\hspace{0.05cm}.$$
- Da hier das Nutzsignal $X$ auf $±1$ normiert ist ⇒ Leistung $1$ anstelle von $P_X$, muss die Varianz des AWGN–Rauschens $N$ in gleicher Weise normiert werden: $σ^2 = P_N/P_X$.
- Der Empfänger trifft aus der reellwertigen Zufallsgröße $Y$ (am AWGN–Kanalausgang) eine Maximum–Likelihood–Entscheidung. Der Empfängerausgang $V$ ist binär $(0$ oder $1)$.
Ausgehend von diesem Modell berechnen wir nun die Kanalkapazität des AWGN–Kanals.
Diese lautet bei einer binären Eingangsgröße $X$ allgemein unter Berücksichtigung von $\text{Pr}(X = -1) = 1 - \text{Pr}(X = +1)$:
- $$C_{\rm BPSK} = \max_{ {\rm Pr}({X} =+1)} \hspace{-0.15cm} I(X;Y) \hspace{0.05cm}.$$
Aufgrund des symmetrischen Kanals ist offensichtlich, dass die Eingangswahrscheinlichkeiten
- $${\rm Pr}(X =+1) = {\rm Pr}(X =-1) = 0.5 $$
zum Optimum führen werden. Gemäß der Seite Transinformationsberechnung bei additiver Störung gibt es mehrere Berechnungsmöglichkeiten:
- $$ \begin{align*}C_{\rm BPSK} & = h(X) + h(Y) - h(XY)\hspace{0.05cm},\\ C_{\rm BPSK} & = h(Y) - h(Y|X)\hspace{0.05cm},\\ C_{\rm BPSK} & = h(X) - h(X|Y)\hspace{0.05cm}. \end{align*}$$
Alle Ergebnisse sind noch um die Pseudo–Einheit „bit/Kanalzugriff” zu ergänzen. Wir wählen hier die mittlere Gleichung:
- Die hierfür benötigte bedingte differentielle Entropie ist gleich
- $$h(Y\hspace{0.03cm}|\hspace{0.03cm}X) = h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm}(2\pi{\rm e}\cdot \sigma^2) \hspace{0.05cm}. $$
- Die differentielle Entropie $h(Y)$ ist vollständig durch die WDF $f_Y(y)$ gegeben. Mit den vorne definierten und skizzierten bedingten Wahrscheinlichkeitsdichtefunktionen erhält man:
- $$f_Y(y) = {1}/{2} \cdot \big [ f_{Y\hspace{0.03cm}|\hspace{0.03cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}{X}=-1) + f_{Y\hspace{0.03cm}|\hspace{0.03cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}{X}=+1) \big ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} h(Y) \hspace{-0.01cm}=\hspace{0.05cm} -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
Es ist offensichtlich, dass $h(Y)$ nur durch numerische Integration ermittelt werden kann, insbesondere, wenn man berücksichtigt, dass sich $f_Y(y)$ im Überlappungsbereich aus der Summe der beiden bedingten Gauß–Funktionen ergibt.
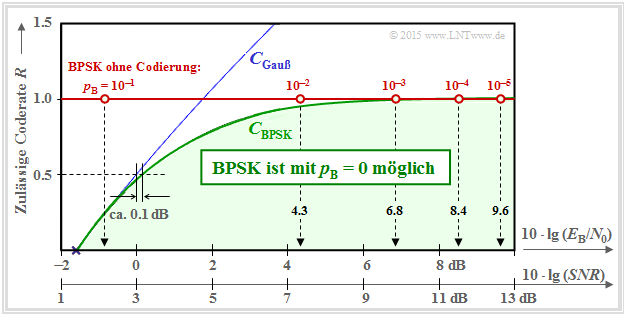
In der folgenden Grafik sind über der Abszisse $10 · \lg (E_{\rm B}/N_0)$ drei Kurven dargestellt:
- die blau gezeichnete Kanalkapazität $C_{\rm Gauß}$, gültig für eine Gaußsche Eingangsgröße $X$ ⇒ $M_X → ∞$,
- die grün gezeichnete Kanalkapazität $C_{\rm BPSK}$ für die Zufallsgröße $X = (+1, –1)$, sowie
- die mit „BPSK ohne Codierung” bezeichnete rote Horizontale.
Diese Kurvenverläufe sind wie folgt zu interpretieren:
- Die grüne Kurve $C_{\rm BPSK}$ gibt die maximal zulässige Coderate $R$ von Binary Phase Shift Keying (BPSK) an, bei der für das gegebene $E_{\rm B}/N_0$ durch bestmögliche Codierung die Bitfehlerwahrscheinlichkeit $p_{\rm B} \equiv 0$ möglich ist.
- Für alle BPSK–Systeme mit den Koordinaten $(10 · \lg \ E_{\rm B}/N_0, \ R)$ im „grünen Bereich” ist $p_{\rm B} \equiv 0$ prinzipiell erreichbar. Aufgabe der Nachrichtentechniker ist es, hierfür geeignete Codes zu finden.
- Die BPSK–Kurve liegt stets unter der absoluten Shannon–Grenzkurve $C_{\rm Gauß}$ für $M_X → ∞$ (blaue Kurve). Im unteren Bereich gilt $C_{\rm BPSK} ≈ C_{\rm Gauß}$. Zum Beispiel muss ein BPSK–System mit $R = 1/2$ nur ein um $0.1\ \rm dB$ größeres $E_{\rm B}/N_0$ bereitstellen, als es die (absolute) Kanalkapazität $C_{\rm Gauß}$ fordert.
- Ist $E_{\rm B}/N_0$ endlich, so gilt stets $C_{\rm BPSK} < 1$ ⇒ siehe Aufgabe 4.9Z. Eine BPSK mit $R = 1$ (und somit ohne Codierung) wird also stets eine Bitfehlerwahrscheinlichkeit $p_{\rm B} > 0$ zur Folge haben.
- Die Fehlerwahrscheinlichkeiten eines solchen BPSK–Systems ohne Codierung $($mit $R = 1)$ sind auf der roten Horizontalen angegeben. Um $p_{\rm B} ≤ 10^{–5}$ zu erreichen, benötigt man mindestens $10 · \lg (E_{\rm B}/N_0) = 9.6\ \rm dB$.
- Diese Wahrscheinlichkeiten ergeben sich gemäß dem Kapitel Fehlerwahrscheinlichkeit des optimalen BPSK-Systems im Buch „Digitalsignalübertragung” zu
- $$p_{\rm B} = {\rm Q} \left ( \sqrt{S \hspace{-0.06cm}N\hspace{-0.06cm}R}\right ) \hspace{0.45cm} {\rm mit } \hspace{0.45cm} S\hspace{-0.06cm}N\hspace{-0.06cm}R = 2\cdot E_{\rm B}/{N_0} \hspace{0.05cm}. $$
Hinweise:
- In obiger Grafik ist als zweite, zusätzliche Abszissenachse $10 · \lg (SNR)$ eingezeichnet.
- Die Funktion ${\rm Q}(x)$ bezeichnet man als die komplementäre Gaußsche Fehlerfunktion.
Vergleich zwischen Theorie und Praxis
Anhand zweier Grafiken soll gezeigt werden, in wie weit sich etablierte Kanalcodes der BPSK–Kanalkapazität (grüne Kurve) annähern. Als Ordinate aufgetragen ist die Rate $R = k/n$ dieser Codes bzw. die Kapazität $C$ (wenn noch die Pseudo–Einheit „bit/Kanalzugriff” hinzugefügt wird).
Vorausgesetzt ist:
- der AWGN–Kanal, gekennzeichnet durch $10 · \lg (E_{\rm B}/N_0)$ in dB, und
- für die durch Kreuze markierten realisierten Codes eine Bitfehlerrate (BER) von $10^{–5}$.
Zu beachten ist, dass die Kanalkapazitätskurven stets für $n → ∞$ und $\rm BER \equiv 0$ gelten.
- Würde man diese strenge Forderung „feherfrei” auch an die betrachteten Kanalcodes endlicher Codelänge $n$ anlegen, so wäre hierfür stets $10 · \lg \ (E_{\rm B}/N_0) \to \infty$ erforderlich.
- Dies ist aber ein eher akademisches Problem, also wenig praxisrelevant. Für $\text{BER} = 10^{–10}$ ergäbe sich eine qualitativ ähnliche Grafik.
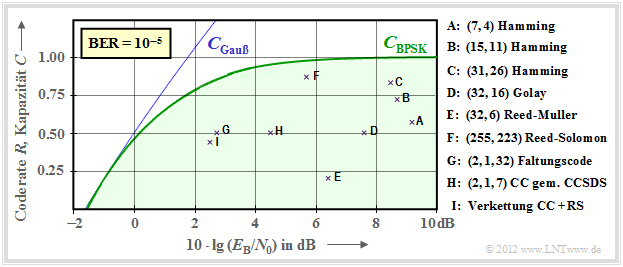
$\text{Beispiel 4:}$ In der Grafik sind die Kenndaten von frühen Systemen mit Kanalcodierung und klassischer Decodierung angegeben.
- Es folgen einige Erläuterungen zu den Daten, die der Vorlesung [Liv10][1] entnommen wurden.
- Die Links bei diesen Erläuterungen beziehen sich oft auf das $\rm LNTwww$–Buch Channel Coding.
- Die Punkte $\rm A$, $\rm B$ und $\rm C$ markieren Hamming–Codes der Raten $R = 4/7 ≈ 0.57$, $R ≈ 0.73$ bzw. $R ≈ 0.84$. Für $\text{BER} = 10^{–5}$ benötigen diese sehr frühen Codes (aus dem Jahr 1950) alle $10 · \lg (E_{\rm B}/N_0) > 8\ \rm dB$.
- Die Markierung $\rm D$ kennzeichnet den binären Golay–Code mit der Rate $R = 1/2$ und der Punkt $\rm E$ einen Reed–Muller–Code. Dieser sehr niederratige Code kam bereits 1971 bei der Raumsonde Mariner 9 zum Einsatz.
- Die Reed–Solomon–Codes (RS–Codes, ca. 1960) sind eine Klasse zyklischer Blockcodes. $\rm F$ markiert einen RS–Code der Rate $223/255 \approx 0.875$ und einem erforderlichen $E_{\rm B}/N_0 < 6 \ \rm dB$.
- $\rm G$ und $\rm H$ bezeichnen zwei Faltungscodes $($englisch: Convolutional Codes, $\rm CC)$ mittlerer Rate. Der Code $\rm G$ wurde schon 1972 bei der Pioneer 10–Mission eingesetzt.
- Die Kanalcodierung der Voyager–Mission Ende der 1970er Jahre ist mit $\rm I$ markiert. Es handelt sich um die Verkettung eines $\text{(2, 1, 7)}$–Faltungscodes mit einem Reed–Solomon–Code.
Anzumerken ist, dass bei den Faltungscodes der dritte Kennungsparameter eine andere Bedeutung hat als bei den Blockcodes. So weist beispielsweise die Kennung $\text{(2, 1, 32)}$ auf das Memory $m = 32$ hin.
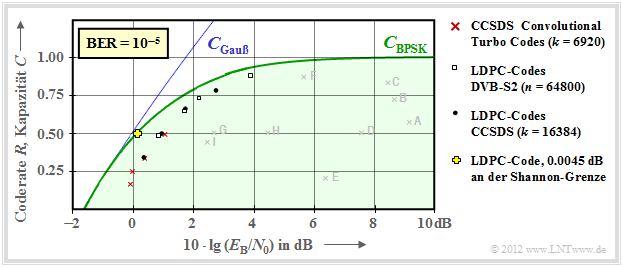
$\text{Beispiel 5:}$ Die im $\text{Beispiel 4}$ genannten frühen Kanalcodes liegen noch relativ weit von der Kanalkapazitätskurve entfernt.
Dies war wahrscheinlich auch ein Grund, warum dem Autor dieses Lerntutorials die auch große praktische Bedeutung der Informationstheorie verschlossen blieb, als er diese Anfang der 1970er Jahre im Studium kennengelernt hat.
Die Sichtweise hat sich deutlich verändert, als in den 1990er Jahren sehr lange Kanalcodes zusammen mit iterativer Decodierung aufkamen. Die neuen Markierungspunkte liegen deutlich näher an der Kapazitätsgrenzkurve.
Hier noch einige Erläuterungen zu dieser Grafik:
- Rote Kreuze markieren die so genannten Turbo–Codes nach $\rm CCSDS$ (Consultative Committee for Space Data Systems) mit jeweils $k = 6920$ Informationsbit und unterschiedlichen Codelängen $n = k/R$. Diese von Claude Berrou um 1990 erfundenen Codes können iterativ decodiert werden. Die (roten) Markierungen liegen jeweils weniger als $1 \ \rm dB$ von der Shannon–Grenze entfernt.
- Ähnlich verhalten sich die LDPC–Codes (Low Density Parity–check Codes) mit konstanter Codelänge $n = 64800$ ⇒ weiße Rechtecke). Sie werden seit 2006 bei DVB–S2 (Digital Video Broadcast over Satellite) eingesetzt und eignen sich aufgrund der spärlichen Einsen–Belegung der Prüfmatrix sehr gut für die iterative Decodierung mittels Faktor–Graphen und Exit Charts.
- Schwarze Punkte markieren die von $\rm CCSDS$ spezifizierten LDPC–Codes mit konstanter Anzahl an Informationsbits $(k = 16384)$ und variabler Wortlänge $n = k/R$. Diese Codeklasse erfordert ein ähnliches $E_{\rm B}/N_0$ wie die roten Kreuze und die weißen Rechtecke.
- Um das Jahr 2000 hatten viele Forscher den Ehrgeiz, sich der Shannon–Grenze bis auf Bruchteile von einem $\rm dB$ anzunähern. Das gelbe Kreuz markiert ein solches Ergebnis $(0.0045 \ \rm dB)$ von [CFRU01][2] mit einem irregulären LDPC–Code der Rate $ R =1/2$ und der Länge $n = 10^7$.
$\text{Fazit:}$ An dieser Stelle soll nochmals die Brillanz und der Weitblick von Claude E. Shannon hervorgehoben werden:
- Er hat 1948 eine bis dahin nicht bekannte Theorie entwickelt, mit der die Möglichkeiten, aber auch die Grenzen der Digitalsignalübertragung aufgezeigt werden.
- Zu dieser Zeit waren die ersten Überlegungen zur digitalen Nachrichtenübertragung gerade mal zehn Jahre alt ⇒ Pulscodemodulation (Alec Reeves, 1938) und selbst der Taschenrechner kam erst mehr als zwanzig Jahre später.
- Shannon's Arbeiten zeigen uns, dass man auch ohne gigantische Computer Großes leisten kann.
Kanalkapazität des komplexen AWGN–Kanals
Höherstufige Modulationsverfahren können jeweils durch eine Inphase– und eine Quadraturkomponente dargestellt werden. Hierzu gehören zum Beispiel
- die M–QAM ⇒ Quadraturamplitudenmodulation; $M ≥ 4$ quadratisch angeordnete Signalraumpunkte,
- die M–PSK ⇒ $M ≥ 4$ Signalraumpunkte in kreisförmiger Anordnung
Die beiden Komponenten lassen sich im äquivalenten Tiefpassbereich auch als Realteil bzw. Imaginärteil eines komplexen Rauschterms $N$ beschreiben.
- Alle oben genannten Verfahren sind zweidimensional.
- Der (komplexe) AWGN–Kanal stellt somit $K = 2$ voneinander unabhängige Gaußkanäle zur Verfügung.
- Entsprechend der Seite Parallele Gaußsche Kanäle ergibt sich deshalb für die Kapazität eines solchen Kanals:
- $$C_{\text{ Gauß, komplex} }= C_{\rm Gesamt} ( K=2) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X/2}{\sigma^2}) \hspace{0.05cm}.$$
- $P_X$ bezeichnet die gesamte Nutzleistung von Inphase– und Quadraturkomponente.
- Dagegen bezieht sich die Varianz $σ^2$ der Störung nur auf eine Dimension: $σ^2 = σ_{\rm I}^2 = σ_{\rm Q}^2$.
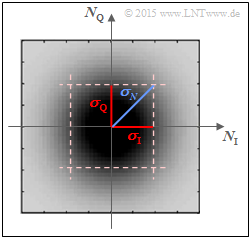
Die Skizze zeigt die 2D–WDF $f_N(n)$ des Gaußschen Rauschprozesses $N$ über den beiden Achsen
- $N_{\rm I}$ (Inphase–Anteil, Realteil) und
- $N_{\rm Q}$ (Quadraturanteil, Imaginärteil).
Dunklere Bereiche der rotationssymmetrischen WDF $f_N(n)$ um den Nullpunkt weisen auf mehr Störanteile hin. Für die Varianz des komplexen Gaußschen Rauschens $N$ gilt aufgrund der Rotationsinvarianz $(σ_{\rm I} = σ_{\rm Q})$ folgender Zusammenhang:
- $$\sigma_N^2 = \sigma_{\rm I}^2 + \sigma_{\rm Q}^2 = 2\cdot \sigma^2 \hspace{0.05cm}.$$
Damit lässt sich die Kanalkapazität auch wie folgt ausdrücken:
- $$C_{\text{ Gauß, komplex} }= {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{\sigma_N^2}) = {\rm log}_2 \hspace{0.1cm} ( 1 + SNR) \hspace{0.05cm}.$$
Die Gleichung wird auf der nächsten Seite numerisch ausgewertet. Man kann aber jetzt schon sagen, dass für das Signal–zu–Störleistungsverhältnis gelten wird:
- $$SNR = {P_X}/{\sigma_N^2} \hspace{0.05cm}.$$
Maximale Coderate für QAM–Strukturen
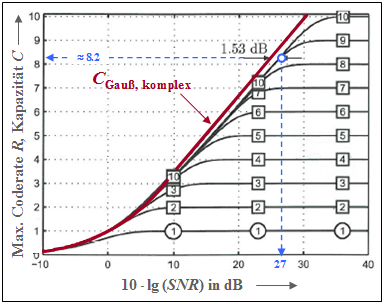
Die Grafik zeigt die Kapazität des komplexen AWGN–Kanals als rote Kurve:
- $$C_{\text{ Gauß, komplex} }= {\rm log}_2 \hspace{0.1cm} ( 1 + SNR) \hspace{0.05cm}.$$
- Die Einheit dieser Kanalkapazität ist „bit/Kanalzugriff” oder „bit/Quellensymbol”.
- Als Abszisse bezeichnet das Signal–zu–Störleistungsverhältnis $10 · \lg (SNR)$ mit ${SNR} = P_X/σ_N^2$.
- Die Grafik wurde [Göb10][3] entnommen. Wir danken Bernhard Göbel, unserem ehemaligen Kollegen am LÜT, für sein Einverständnis, diese Abbildung verwenden zu dürfen, sowie für die große Unterstützung unseres Lerntutorials während seiner gesamten aktiven Zeit.
Die rote Kurve basiert entsprechend der Shannon–Theorie wieder auf einer Gaußverteilung $f_X(x)$ am Eingang. Zusätzlich eingezeichnet sind zehn weitere Kapazitätskurven für wertdiskreten Eingang:
- die Kurve für Binary Phase Shift Keying $($BPSK, mit „1” markiert ⇒ $K = 1)$,
- die $M$–stufige Quadratur–Amplitudenmodulation $($mit $M = 2^K, K = 2$, ... , $10)$.
Man erkennt aus dieser Darstellung:
- Die BPSK–Kurve und alle $M$–QAM–Kurven liegen rechts von der roten Shannon–Grenzkurve. Bei kleinem $SNR$ sind allerdings alle Kurven von der roten Kurve fast nicht mehr zu unterscheiden.
- Der Endwert aller Kurven für wertdiskrete Eingangssignale ist $K = \log_2 (M)$. Für $SNR \to ∞$ erhält man beispielsweise $C_{\rm BPSK} = 1 \ \rm bit/Symbol$ sowie $C_{\rm 4-QAM} = C_{\rm QPSK} = 2\ \rm bit/Symbol$.
- Die blauen Markierungen zeigen, dass eine $\rm 2^{10}–QAM$ mit $10 · \lg (SNR) ≈ 27 \ \rm dB$ eine Coderate von $R ≈ 8.2$ ermöglicht. Der Abstand zur Shannon–Kurve beträgt hier $1.53\ \rm dB$.
- Der Shaping Gain beträgt $10 · \lg (π \cdot {\rm e}/6) = 1.53 \ \rm dB$. Diese Verbesserung lässt sich erzielen, wenn man die Lage der $2^{10} = 32^2$ quadratisch angeordneten Signalraumpunkte so ändert, dass sich eine gaußähnliche Eingangs–WDF ergibt ⇒ Signal Shaping.
$\text{Fazit:}$ In der Aufgabe 4.10 werden die AWGN–Kapazitätskurven von BPSK und QPSK diskutiert:
- Ausgehend von der Abszisse $10 · \lg (E_{\rm B}/N_0)$ mit $E_{\rm B}$ (Energie pro Informationsbit) kommt man zur QPSK–Kurve durch Verdopplung der BPSK–Kurve:
- $$C_{\rm QPSK}\big [10 \cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})\big ] = 2 \cdot C_{\rm BPSK}\big [10 \cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0}) \big ] .$$
- Vergleicht man aber BPSK und QPSK bei gleicher Energie $E_{\rm S}$ pro Informationssymbol, so gilt:
- $$C_{\rm QPSK}[10 \cdot {\rm lg} \hspace{0.1cm}(E_{\rm S}/{N_0})] = 2 \cdot C_{\rm BPSK}[10 \cdot {\rm lg} \hspace{0.1cm}(E_{\rm S}/{N_0}) - 3\,{\rm dB}] .$$
- Hierbei ist berücksichtigt, dass bei QPSK die Energie in einer Dimension nur $E_{\rm S}/2$ beträgt.
Aufgaben zum Kapitel
Aufgabe 4.8: Numerische Auswertung der AWGN-Kanalkapazität
Aufgabe 4.8Z: Was sagt die AWGN-Kanalkapazitätskurve aus?
Aufgabe 4.9: Höherstufige Modulation
Aufgabe 4.9Z: Ist bei BPSK die Kanalkapazität $C ≡ 1$ möglich?
Aufgabe 4.10: QPSK–Kanalkapazität
Quellenverzeichnis
- ↑ Liva, G.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.
- ↑ Chung S.Y; Forney Jr., G.D.; Richardson, T.J.; Urbanke, R.: On the Design of Low-Density Parity- Check Codes within 0.0045 dB of the Shannon Limit. – In: IEEE Communications Letters, vol. 5, no. 2 (2001), pp. 58–60.
- ↑ Göbel, B.: Information–Theoretic Aspects of Fiber–Optic Communication Channels. Dissertation. TU München. Verlag Dr. Hut, Reihe Informationstechnik, ISBN 978-3-86853-713-0, 2010.