Difference between revisions of "Linear and Time Invariant Systems/Laplace Transform and p-Transfer Function"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Beschreibung kausaler realisierbarer Systeme |Vorherige Seite=Folgerungen aus dem Zuordnungssatz |Nächste Seite=Laplace–Rücktransfor…“) |
|||
| Line 8: | Line 8: | ||
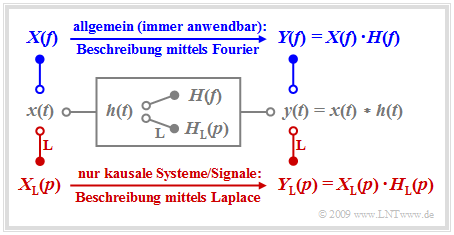
Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort $h(t)$, an dessen Eingang das Signal $x(t)$ anliegt. Das Ausgangssignal $y(t)$ ergibt sich dann als das Faltungsprodukt $x(t) ∗ h(t)$. | Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort $h(t)$, an dessen Eingang das Signal $x(t)$ anliegt. Das Ausgangssignal $y(t)$ ergibt sich dann als das Faltungsprodukt $x(t) ∗ h(t)$. | ||
| − | [[File:P_ID1757__LZI_T_3_2_S1_neu.png | | + | [[File:P_ID1757__LZI_T_3_2_S1_neu.png | 500px|Allgemeines (auch akausales) sowie kausales Systemmodell]] |
Bei akausalen Systemen und Signalen muss zur Beschreibung des Spektralverhaltens stets das erste Fourierintegral angewendet werden, und es gilt für das Ausgangsspektrum: | Bei akausalen Systemen und Signalen muss zur Beschreibung des Spektralverhaltens stets das erste Fourierintegral angewendet werden, und es gilt für das Ausgangsspektrum: | ||
| Line 17: | Line 17: | ||
*Die so behandelten Systeme sind stets durch eine Schaltung realisierbar. Der Entwickler kommt nicht in Versuchung, realitätsfremde Lösungen anzubieten. | *Die so behandelten Systeme sind stets durch eine Schaltung realisierbar. Der Entwickler kommt nicht in Versuchung, realitätsfremde Lösungen anzubieten. | ||
*Die Laplace–Transformierte $X_L(p)$ ist stets eine reelle Funktion der Spektralvariablen $p$. Dass sich diese Variable entsprechend $p = j · 2πf$ aus der Multiplikation der physikalischen Kreisfrequenz $ω = 2πf$ mit der imaginären Einheit j ergibt, spielt für den Anwender keine Rolle. | *Die Laplace–Transformierte $X_L(p)$ ist stets eine reelle Funktion der Spektralvariablen $p$. Dass sich diese Variable entsprechend $p = j · 2πf$ aus der Multiplikation der physikalischen Kreisfrequenz $ω = 2πf$ mit der imaginären Einheit j ergibt, spielt für den Anwender keine Rolle. | ||
| − | *Die implizite Bedingung $x(t) =$ 0 für $t$ < 0 erlaubt speziell die Analyse des Einschwingverhaltens nach Einschaltvorgängen in einfacherer Weise als mit dem Fourierintegral. | + | *Die implizite Bedingung $x(t) =$ 0 für $t$ < 0 erlaubt speziell die Analyse des Einschwingverhaltens nach Einschaltvorgängen in einfacherer Weise als mit dem Fourierintegral. |
| + | |||
| + | ==Definition der Laplace–Transformation== | ||
| + | Ausgehend vom ersten Fourierintegral | ||
| + | $$X(f) = \int\limits_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t$$ | ||
| + | ergibt sich bei einer kausalen Zeitfunktion (wenn also gilt: $x(t) =$ 0 für $t$ < 0) mit der formalen Substitution $p = j · 2πf$ direkt die Laplace–Transformation. | ||
| + | {{Definition}} | ||
| + | Die Laplace–Transformierte einer kausalen Zeitfunktion $x(t)$ lautet: | ||
| + | $$X_{\rm L}(p) = \int\limits_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}$$ . | ||
| + | {{end}} | ||
| + | |||
| + | |||
| + | Der Zusammenhang zwischen der Laplace–Transformierten $X_L(p)$ und dem physikalischen Spektrum $X(f)$ ist häufig wie folgt gegeben: | ||
| + | $$X(f) = X_{\rm L}(p)}\Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j\hspace{0.05cm}2\pi \it f}}.$$ | ||
| + | Beinhaltet allerdings das Signal $x(t)$ periodische Anteile und damit die Spektralfunktion $X(f)$ zusätzliche Diracfunktionen, so ist diese Gleichung nicht anwendbar. In diesem Fall muss $p = α + j · 2πf$ angesetzt werden und es ist dann der Grenzübergang $α → 0$ zu bilden. | ||
| + | {{Beispiel}} | ||
| + | Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion – Skizze – aus: | ||
| + | $$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$ | ||
| + | Damit lautet die Laplace–Transformierte: | ||
| + | $$X_{\rm L}(p) = \int\limits_{0}^{\infty} { {\rm e}^{-t/T}}\hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.05cm}\cdot \hspace{0.05cm}t}}\hspace{0.05cm}\Bigg |_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$ | ||
| + | Mit $p = j · 2πf$ erhält man die herkömmliche Spektralfunktion bezüglich $f$: | ||
| + | $$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ | ||
| + | Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort $h(t)$ sich gegenüber der obigen Zeitfunktion um den Faktor $1/T$ unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte: | ||
| + | $$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.4cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ | ||
| + | Häufig verwendet man dann anstelle des Parameters $T$ die 3dB–Grenzfrequenz $f_G = 1/(2πT)$. | ||
Revision as of 21:25, 8 May 2016
Betrachtetes Systemmodell
Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort $h(t)$, an dessen Eingang das Signal $x(t)$ anliegt. Das Ausgangssignal $y(t)$ ergibt sich dann als das Faltungsprodukt $x(t) ∗ h(t)$.
Bei akausalen Systemen und Signalen muss zur Beschreibung des Spektralverhaltens stets das erste Fourierintegral angewendet werden, und es gilt für das Ausgangsspektrum: $$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$ Das Fourierintegral besitzt auch für kausale Systeme und Signale, also unter der Voraussetzung $$x(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}$$ weiterhin Gültigkeit. In diesem Fall ergeben sich aber durch Anwendung der Laplace–Transformation unter Beachtung gewisser Restriktionen wesentliche Vorteile:
- Die so behandelten Systeme sind stets durch eine Schaltung realisierbar. Der Entwickler kommt nicht in Versuchung, realitätsfremde Lösungen anzubieten.
- Die Laplace–Transformierte $X_L(p)$ ist stets eine reelle Funktion der Spektralvariablen $p$. Dass sich diese Variable entsprechend $p = j · 2πf$ aus der Multiplikation der physikalischen Kreisfrequenz $ω = 2πf$ mit der imaginären Einheit j ergibt, spielt für den Anwender keine Rolle.
- Die implizite Bedingung $x(t) =$ 0 für $t$ < 0 erlaubt speziell die Analyse des Einschwingverhaltens nach Einschaltvorgängen in einfacherer Weise als mit dem Fourierintegral.
Definition der Laplace–Transformation
Ausgehend vom ersten Fourierintegral $$X(f) = \int\limits_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t$$ ergibt sich bei einer kausalen Zeitfunktion (wenn also gilt: $x(t) =$ 0 für $t$ < 0) mit der formalen Substitution $p = j · 2πf$ direkt die Laplace–Transformation.
Die Laplace–Transformierte einer kausalen Zeitfunktion $x(t)$ lautet: $$X_{\rm L}(p) = \int\limits_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}$$ .
Der Zusammenhang zwischen der Laplace–Transformierten $X_L(p)$ und dem physikalischen Spektrum $X(f)$ ist häufig wie folgt gegeben:
$$X(f) = X_{\rm L}(p)}\Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j\hspace{0.05cm}2\pi \it f}}.$$
Beinhaltet allerdings das Signal $x(t)$ periodische Anteile und damit die Spektralfunktion $X(f)$ zusätzliche Diracfunktionen, so ist diese Gleichung nicht anwendbar. In diesem Fall muss $p = α + j · 2πf$ angesetzt werden und es ist dann der Grenzübergang $α → 0$ zu bilden.
Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion – Skizze – aus: $$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$ Damit lautet die Laplace–Transformierte: $$X_{\rm L}(p) = \int\limits_{0}^{\infty} { {\rm e}^{-t/T}}\hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.05cm}\cdot \hspace{0.05cm}t}}\hspace{0.05cm}\Bigg |_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$ Mit $p = j · 2πf$ erhält man die herkömmliche Spektralfunktion bezüglich $f$: $$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort $h(t)$ sich gegenüber der obigen Zeitfunktion um den Faktor $1/T$ unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte: $$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.4cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ Häufig verwendet man dann anstelle des Parameters $T$ die 3dB–Grenzfrequenz $f_G = 1/(2πT)$.