Contents
- 1 Generalized system functions of time variant systems
- 2 Simplifications due to the GWSSUS requirements
- 3 Autocorrelation function of the time variant impulse response
- 4 Power spectral density of the time variant impulse response
- 5 ACF and PSD of the frequency-variant transfer function
- 6 ACF and PSD of the delay Doppler function
- 7 AKF und LDS der zeitvarianten Übertragungsfunktion
- 8 Kenngrößen des GWSSUS–Modells
- 9 Simulation gemäß dem GWSSUS–Modell
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
Generalized system functions of time variant systems
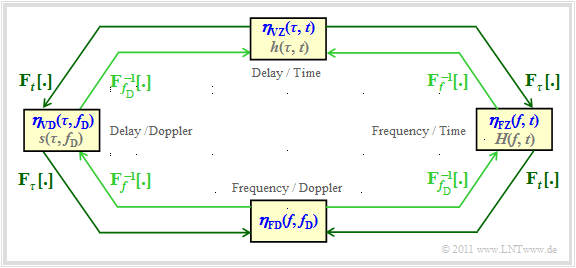
Linear time-invariant systems $\rm (LTI)$ can be completely described with only two system functions, the transfer function $H(f)$ and the impulse response $h(t)$ – $h(\tau)$ after renaming –, in contrast, four different functions are possible with time-variant systems $\rm (LTV)$ . There is no formal differentiation of these functions with regard to time and frequency domain representation by a lowercase and uppercase letters.
Therefore a nomenclature change will be made, which can be formalized as follows:
- The four possible system functions are uniformly denoted by $\boldsymbol{\eta}_{12}$ .
- The first subindex is either a $\boldsymbol{\rm V}$ $($delay time $\tau)$ or a $\boldsymbol{\rm F}$ $($frequency $f)$.
- Either a $\boldsymbol{\rm Z}$ $($Time $t)$ or a $\boldsymbol{\rm D}$ $($Doppler frequency $f_{\rm D})$ is possible as the second subindex.
Since, in contrast to line-based transmission, the system functions of mobile communications cannot be described deterministically, but are statistical variables, the corresponding correlation functions must be considered later on.
In the following, we will refer to these as $\boldsymbol{\varphi}_{12}$, and use the same indices as for the system functions $\boldsymbol{\eta}_{12}$.
These formalized designations are inscribed in the graphic in blue letters.
- Additionally, the designations used in other chapters or literature are given (grey letters).
- In the other chapters these are also partly used.
- At the top you can see the time variant impulse response ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t) \equiv h(\tau,\hspace{0.05cm} t)$ in the delay–time range. The associated autocorrelation function (ACF) is
- \[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \big[ \eta_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \big]\hspace{0.05cm}. \]
- For the frequency–time representation you get the time-variant transfer function ${\eta}_{\rm FZ}(f,\hspace{0.05cm} t) \equiv H(f,\hspace{0.05cm} t)$. The Fourier transform with respect to $\tau$ is represented in the graph by ${\rm F}_\tau\hspace{0.05cm}[ \cdot ]$ . The Fourier integral is written out in full:
- \[\eta_{\rm FZ}(f, \hspace{0.05cm} t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau,\hspace{0.05cm} t) \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}, \hspace{0.3cm} \text{kurz:} \hspace{0.2cm} \eta_{\rm FZ}(f, t) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm} \tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t) \hspace{0.05cm}.\]
The ACF of this time variant transfer function is general:
- \[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \big [ \eta_{\rm FZ}(f_1, t_1) \cdot \eta_{\rm FZ}^{\star}(f_2, t_2) \big ]\hspace{0.05cm}.\]
- The Scatter–Function ${\eta}_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D}) \equiv s(\tau,\hspace{0.05cm} f_{\rm D})$ corresponding to the left block describes the mobile communications channel in the Delay–Doppler Area. The function parameter $f_{\rm D}$ describes the Doppler frequency. The scatter function results from the time variant impulse response ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t)$ through Fourier transformation with respect to the second parameter $t$:
- \[ \eta_{\rm VD}(\tau, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm VD}(\tau_1, f_{\rm D_1}) \cdot \eta_{\rm VD}^{\star}(\tau_2, f_{\rm D_2}) \right ] \hspace{0.05cm}.\]
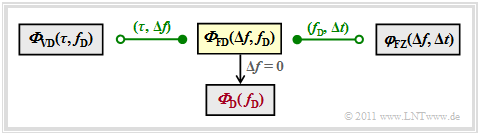
- Finally, we consider the so-called frequency-variant transfer function, i.e. the frequency–Doppler representation. According to the graph, this can be reached in two ways:
- \[\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm FZ}(f, t)\hspace{0.05cm},\]
- \[\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VD}(\tau, f_{\rm D})\hspace{0.05cm}.\]
$\text{Hints:}$
- The specified Fourier correlations between the system functions in the graph are illustrated by the outer, dark green arrows and are marked with ${\rm F}_p\hspace{0.05cm}[\hspace{0.05cm} \cdot \hspace{0.05cm}]$ . $p$ indicates to which parameter $\tau$, $f$, $t$ or $f_{\rm D}$ does the Fourier transformation refer.
- The inner (lighter) arrows indicate the links via the inverse Fourier transform (inverse Fourier transform). For this we use the notation ${ {\rm F}_p}^{-1}\hspace{0.05cm}[ \hspace{0.05cm} \cdot \hspace{0.05cm} ]$.
- The applet Impulses and Spectra illustrates the connection between the time and frequency domain, which can be described by formulas using Fourier transformation and Fourier inverse transformation.
Simplifications due to the GWSSUS requirements
The general relationship between the four system functions is very complicated due to non-stationary effects.
Compared to the general model, some limitations have to be made in order to arrive at a suitable model for the mobile communications channel from which relevant statements for practical applications can be derived.
The following definitions lead to the $\rm GWSSUS$ model
$( \rm G$aussian $\rm W$ide $\rm S$ense $\rm S$tationary $\rm U$ncorrelated $\rm S$cattering$)$:
- The random process of the channel impulse response $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$ is generally assumed to be complex (i.e., description in the equivalent low-pass range), Gaussian $($identifier $\rm G)$ and zero-mean (Rayleigh, not Rice, that means, no line of sight) .
- The random process is weakly stationary ⇒ its characteristics change only slightly with time, and the ACF $ {\varphi}_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1,\hspace{0.05cm}\tau_2,\hspace{0.05cm} t_2)$ of the time variant impulse response does not depend on the absolute times $t_1$ and $t_2$ but only on the time difference $\Delta t = t_2 - t_1$. This is indicated by the identifier $\rm WSS$ ⇒ $\rm W$ide $\rm S$ense $\rm S$tationary.
- The individual echoes due to multipath propagation are uncorrelated, which is expressed by the identifier $\rm US$ ⇒ $\rm U$ncorrelated $\rm S$cattering.
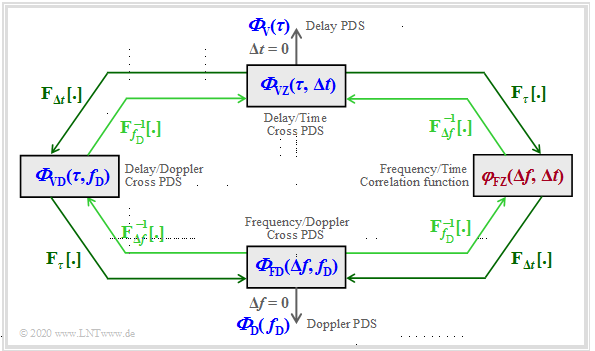
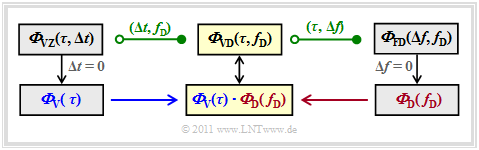
The mobile communications channel can be described in full according to this graph. The individual power density spectra (labeled blue) and the correlation function (labeled red) is explained in detail in the following pages.
Autocorrelation function of the time variant impulse response
We now consider the Autocorrelation Function $\rm (ACF)$ of the time variant impulse response ⇒ $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$ more closely. It shows
- Based on the $\rm WSS$ property, the autocorrelation function can be written with $\Delta t = t_2 - t_1$ :
- \[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = \varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t)\hspace{0.05cm}.\]
- Since the echoes were assumed to be independent of each other $\rm (US$ property$)$, the impulse response can be assumed to be uncorrelated with respect to the delays $\tau_1$ and $\tau_2$ Then:
- \[\varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t) = 0 \hspace{0.35cm}{\rm f\ddot{u}r}\hspace{0.35cm} \tau_1 \ne \tau_2\hspace{0.05cm}. \]
- If one now replaces $\tau_1$ with $\tau$ and $\tau_2$ with $\tau + \Delta \tau$, this autocorrelation function can be represented in the following way:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. \]
- Because of the convolution property of the Dirac function, the ACF for $\tau_1 \ne \tau_2$ ⇒ $\Delta \tau \ne 0$ disappears.
- $ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.1cm}$ is the delay–time–cross power spectrual density , which depends on the delay $\tau \ (= \tau_1 =\tau_2)$ and on the time difference $\Delta t = t_2 - t_1$ .
$\text{Please note:}$
- With this approach, autocorrelation function $\varphi_{\rm VZ}(\Delta \tau, \Delta t)$ and power spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ are not connected via the Fourier transform as usual, but are linked via a Dirac function:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. \]
- Not all symmetry properties that follow from the Wiener–Chintchine–Theorem are thus given here. In particular it is quite possible and even very likely that such a power spectral density is an odd function.
In the overview on the last page, the Delay–Time Cross power spectral density ${\it \Phi}_{\rm VZ}(\tau, \delta t) $ can be seen in the top middle.
- Since $\eta_{\rm VZ}(\tau, t) $ ,like any Impulse Response, has the unit $\rm [1/s]$ , the autocorrelation function has the unit $\rm [1/s^2]$:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = {\rm E} \left [ \eta_{\rm VZ}(\tau, t) \cdot \eta_{\rm VZ}^{\star}(\tau + \Delta \tau, t + \Delta t) \right ].\]
- But since the Dirac function with the time argument $\delta(\Delta \tau)$ also has the unit $\rm [1/s]$ the delay–time–cross power spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ also has the unit $\rm [1/s]$:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.\]
Power spectral density of the time variant impulse response
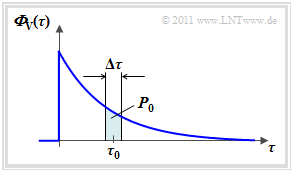
One obtains the Delay–power spectral density ${\it \Phi}_{\rm V}(\Delta \tau)$ by setting the second parameter ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$ in the function $\Delta t = 0$ . The graphic on the right shows an exemplary curve.
The delay–power spectral density is a central quantity for the description of the mobile communications channel. This has the following characteristics:
- ${\it \Phi}_{\rm V}(\Delta \tau_0)$ is a measure for the "power" of those signal components which are delayed by $\tau_0$ . For this purpose, an implicit averaging over all Doppler frequencies $(f_{\rm D})$ is carried out.
- The delay–power spectral density ${\it \Phi}_{\rm V}(\Delta \tau)$ has, like ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$ , the unit $\rm [1/s]$. It characterizes the power distribution over all possible delay times $\tau$.
- In the above graphic, the power $ P_0 \approx {\it \Phi}_{\rm V}(\Delta \tau_0)\cdot \Delta \tau$ of those signal components that arrive at the receiver via any path with a delay between $\tau_0 \pm \Delta \tau/2$
- Normalizing the power spectral density ${\it \Phi}_{\rm V}(\Delta \tau)$ in such a way that the area is $1$ results in the probability density function $\rm (PDF)$ of the delay time:
- \[{\rm PDF}_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau)}{\int_{0 }^{\infty}{\it \Phi}_{\rm V}(\tau)\hspace{0.15cm}{\rm d}\tau} \hspace{0.05cm}.\]
Note on nomenclature:
- In the book "Stochastic Signal Theory" we would have denoted this Probability Density Function with $f_\tau(\tau)$ .
- To make the connection between ${\it \Phi}_{\rm V}(\Delta \tau)$ and the PDF clear and to avoid confusion with the frequency $f$ we use the nomenclature given here.
$\text{Example 1: Delay models according to COST 207}$
In the 1990s, the European Union founded the working group COST 207 with the aim to provide standardized channel models for cellular mobile communications. where "COST" stands for European Cooperation in Science and Technology.
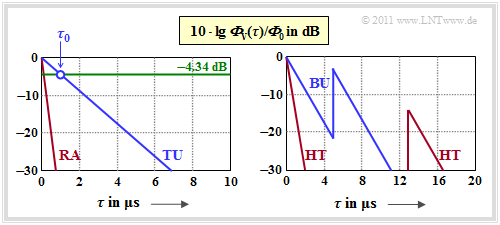
In this international committee profiles for the delay time $\tau$ have been developed, based on measurements and valid for different application scenarios. In the following, four different delay–power spectral densities are given, where the normalization factor ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ is always used. The graph shows the delay–power density of these profiles in logarithmic representation:
(1) profile $\rm RA$ (Rural Area) ⇒ rural area:
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.3cm}{\rm in \hspace{0.15cm}range}\hspace{0.3cm} 0 < \tau < 0.7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.109\,{\rm µ s}\hspace{0.05cm}.\]
(2) profile $\rm TU$ (Typical Urban) ⇒ cities and suburbs:
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.3cm}{\rm in \hspace{0.15cm}range}\hspace{0.3cm} 0 < \tau < 7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}.\]
(3) profile $\rm BU$ (Bad Urban) ⇒ unfavourable conditions in cities:
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.5 \cdot {\rm e}^{ (5\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{0.1cm} {\rm für}\hspace{0.3cm} 0 < \tau < 5\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}, \\ \hspace{0.1cm} {\rm für}\hspace{0.3cm} 5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}\]
(4) profile $\rm HT$ (Hilly Terrain) ⇒ hilly and mountainous regions:
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.04 \cdot {\rm e}^{ (15\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{-0.25cm} {\rm für}\hspace{0.3cm} 0 < \tau < 2\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.286\,{\rm µ s}\hspace{0.05cm}, \\ \hspace{-0.25cm} {\rm for}\hspace{0.3cm} 15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}\]
One can tell from the graphics:
- The exponential functions in linear representation now become straight lines.
- For logarithmic display, you can read the PSD parameter $\tau_0$ for $\rm 10 \cdot lg \ (1/e) = -4.34 \ dB$ as shown in the graph for the $\rm TU$ profile.
- These four COST–profiles are described in the Excercise 2.8 in more detail.
ACF and PSD of the frequency-variant transfer function
The system function $\eta_{\rm FD}(f, f_{\rm D})$ described in the nbsp; overview on the first page of this chapter is also known as the frequency-variant transfer function where the adjective "frequency-variant" refers to the Doppler frequency
The associated ACF is defined as follows:
- \[\varphi_{\rm FD}(f_1, f_{\rm D_1}, f_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm FD}(f_1, f_{\rm D_1}) \cdot \eta_{\rm FZ}^{\star}(f_2, f_{\rm D_2}) \right ]\hspace{0.05cm}. \]
By similar considerations as on the previous page this autocorrelation function can be represented under GWSSUS–conditions as follows
- \[\varphi_{\rm FD}(\Delta f, \Delta f_{\rm D}) = \delta(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \hspace{0.05cm}.\]
The following applies:
- ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ is the so-called frequency–Doppler–cross power spectral density, which is highlighted in the graphic at the end of the page by a yellow background.
- The first argument $\Delta f = f_2 - f_1$ takes into account that ACF and PSD depend only on the frequency difference due to the stationarity .
- The factor $\delta (\Delta f_{\rm D})$ with $\Delta f_{\rm D} = f_{\rm D_2} - f_{\rm D_1}$ expresses the uncorrelation of the PSD with respect to the Doppler shift.
- You get from ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ to Doppler–Power Spectral Density ${\it \Phi}_{\rm D}(f_{\rm D})$ if you set $\Delta f= 0$
- The Doppler–power spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$ indicates the power with which individual Doppler frequencies occur.
- The probability density of the Doppler frequency is obtained from ${\it \Phi}_{\rm D}(f_{\rm D})$ by suitable surface normalization. The PDF has like ${\it \Phi}_{\rm D}(f_{\rm D})$ the unit $\rm [1/Hz]$
- \[{\rm PDF}_{\rm D}(f_{\rm D}) = \frac{{\it \Phi}_{\rm D}(f_{\rm D})}{\int_{-\infty }^{+\infty}{\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.15cm}{\rm d}f_{\rm D}} \hspace{0.05cm}.\]
- Often, for example for a vertical monopulse antenna in an isotropically scattered field, the ${\it \Phi}_{\rm D}(f_{\rm D})$ given through the Jakes–spectrum .
The frequency–Doppler–cross power spectral density ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ is highlighted in yellow.
- The Fourier connections to the neighboring GWSSUS–system description functions are also marked.
- We refer here to the interactive applet To_clarify_the_Doppler_effect.
ACF and PSD of the delay Doppler function
The system function shown in the Overview on the first page of this chapter on the left hand side was named $\eta_{\rm VD}(\tau, f_{\rm D})$ . The ACF of this delay–Doppler–function can be written with $\Delta \tau = \tau_2 - \tau_1$ and $\Delta f_{\rm D} = f_{\rm D2} - f_{\rm D1}$ taking into account the GWSSUS properties with $\Delta \tau = \tau_2 - \tau_1$ and $\Delta f_{\rm D}{\rm D2} = f_{\rm D2} - f_{\rm D1}$ as follows
- \[\varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = \varphi_{\rm VD}(\Delta \tau, \Delta f_{\rm D}) = \delta(\Delta \tau) \cdot {\rm \delta}(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm VD}(\tau, f_{\rm D}) \hspace{0.05cm}.\]
It should be noted about this equation:
- The first Dirac function $\delta (\delta \tau)$ takes into account that the delays are uncorrelated ("Uncorrelated Scattering").
- The second Dirac function $\delta (\Delta f_{\rm D})$ follows from the stationarity ("Wide Sense Stationary").
- The delay–Doppler–power spectral density ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ – also called Scatter–LDS – can be derived from ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$ or ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ :
- \[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) ={\rm F}_{\Delta t} \big [ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \big ] = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm VZ}(\tau, \Delta t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm D} \hspace{0.05cm}\cdot \hspace{0.05cm}\Delta t}\hspace{0.15cm}{\rm d}\Delta t \hspace{0.05cm},\]
- \[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\rm F}_{f_{\rm D}}^{-1} \big [ {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \big ] = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \cdot {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \tau \hspace{0.05cm}\cdot \hspace{0.05cm} \Delta f}\hspace{0.15cm}{\rm d}\Delta f \hspace{0.05cm}. \]
- Both the system function $\eta_{\rm VD}(\tau, f_{\rm D})$ and the derived functions $\varphi _{\rm VD}(\delta \tau, \delta f_{\rm D})$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ are dimensionless. For more information on this, see the specification for Excercise 2.6.
- Furthermore, if the GWSSUS requirements are met, the scatter function is equal to the product of the delay's and Doppler's power spectral densities:
- \[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.\]
$\text{Fazit:}$ Die Abbildung fasst die bisherigen Ergebnisse dieses Kapitels zusammen.
Festzuhalten ist:
(1) Der Einfluss der Verzögerungszeit (Laufzeit) $\tau$ und der Dopplerfrequenz $f_{\rm D}$ lässt sich separieren
- in das blaue Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$, und
- das rote Leistungsdichtespektrum ${\it \Phi}_{\rm D}(f_{\rm D})$.
(2) Das 2D–Verzögerungs–Doppler–Leistungsdichtespektrum ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ ist gleich dem Produkt aus diesen beiden Anteilen.
AKF und LDS der zeitvarianten Übertragungsfunktion
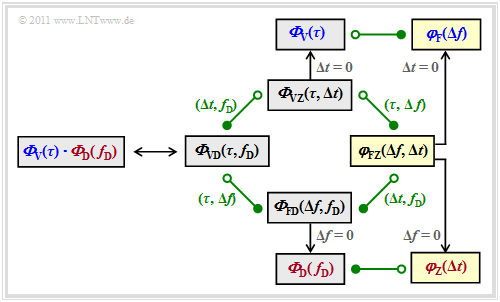
Die folgende Grafik zeigt alle Zusammenhänge zwischen den einzelnen Leistungsdichtespektren nochmals in kompakter Form.
Auf den letzten Seiten wurden dabei bereits behandelt:
- $${\it \Phi}_{\rm VZ}(\tau, \Delta t)\hspace{0.55cm}\Rightarrow \hspace{0.3cm}\text{mit} \hspace{0.2cm}\Delta t = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau),$$
- $${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{mit} \hspace{0.2cm}\Delta f = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm D}( f_{\rm D}),$$
- $${\it \Phi}_{\rm VD}(\tau, f_{\rm D})= {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.$$
Bisher noch nicht betrachtet wurde die Frequenz–Zeit–Korrelationsfunktion
(in nebenstehender Grafik gelb markiert):
- \[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \left [ \eta_{\rm FZ}(f_1, t_1) \cdot \eta_{\rm FZ}^{\star}(f_2, t_2) \right ]\hspace{0.05cm}.\]
Berücksichtigt man wieder die GWSSUS–Vereinfachungen sowie die Identität $\eta_{\rm FZ}(f, \hspace{0.05cm}t) = H(f, \hspace{0.05cm}t)$, so lässt sich die AKF mit $\Delta f = f_2 - f_1$ und $\Delta t = t_2 - t_1$ auch wie folgt schreiben:
- \[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\varphi_{\rm FZ}(\Delta f, \Delta t) = {\rm E} \big [ H(f, t) \cdot H^{\star}(f + \Delta f, t + \Delta t) \big ]\hspace{0.05cm}.\]
Hierzu ist anzumerken:
- Schon an der Namensgebung ist zu erkennen, dass $\varphi_{\rm FZ}(\Delta f, \Delta t)$ eine Korrelationsfunktion ist und kein Leistungsdichtespektrum wie die Funktionen ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$, ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ und ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$.
- Die Fourierzusammenhänge mit den benachbarten Funktionen lauten:
- \[{\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.2cm} \stackrel{\tau, \hspace{0.05cm}\Delta f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \varphi_{\rm FZ}(\Delta f, \hspace{0.05cm}\Delta t) \hspace{0.2cm} \stackrel{\Delta t,\hspace{0.05cm} f_{\rm D}}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} {\it \Phi}_{\rm FD}(\Delta f,\hspace{0.05cm} f_{\rm D}) \hspace{0.05cm}.\]
- Setzt man in dieser 2D– Funktion die Parameter $\Delta t = 0$ bzw. $\Delta f = 0$, so ergeben sich die separaten Korrelationsfunktionen für den Frequenz– bzw. den Zeitbereich:
- \[\varphi_{\rm F}(\Delta f) = \varphi_{\rm FZ}(\Delta f, \Delta t = 0) \hspace{0.05cm},\]
- \[\varphi_{\rm Z}(\Delta t) = \varphi_{\rm FZ}(\Delta f = 0, \Delta t ) \hspace{0.05cm}.\]
- Aus obiger Grafik wird auch deutlich, dass diese Korrelationsfunktionen mit den hergeleiteten Leistungsdichtespektren über die Fouriertransformation korrespondieren:
- \[\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm},
\hspace{0.4cm}\varphi_{\rm Z}(\Delta t) \hspace{0.2cm} {\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.\]
Kenngrößen des GWSSUS–Modells
Entsprechend den Ergebnissen der letzten Seite wird der Mobilfunkkanal durch
- das Verzögerungs–Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$ und
- das Doppler–Leistungsdichtespektrum ${\it \Phi}_{\rm D}(f_{\rm D})$
vollständig beschrieben. Durch geeignete Normierung auf die jeweilige Fläche $1$ ergeben sich daraus die Dichtefunktionen bezüglich der Verzögerungszeit $\tau$ bzw. der Dopplerfrequenz $f_{\rm D}$.
Aus den Leistungsdichtespektren bzw. den zugehörigen Korrelationsfunktionen können Kenngrößen abgeleitet werden. Die wichtigsten sind hier zusammengestellt:
$\text{Definition:}$ Die Mehrwegeverbreiterung (englisch: Time Delay Spread oder Multipath Spread ) $T_{\rm V}$ gibt die Verbreiterung an, die ein Diracimpuls durch den Kanal im statistischen Mittel erfährt. $T_{\rm V}$ ist definiert als die Standardabweichung $(\sigma_{\rm V})$ der Zufallsgröße $\tau$:
- \[T_{\rm V} = \sigma_{\rm V} = \sqrt{ {\rm E} \big [ \tau^2 \big ] - m_{\rm V}^2} \hspace{0.05cm}.\]
- Der Mittelwert $m_{\rm V} = {\rm E}\big[\tau \big]$ ist eine für alle Signalanteile „gleiche mittlere Laufzeit” (englisch: Average Excess Delay).
- ${\rm E} \big [ \tau^2 \big ] $ ist als quadratischer Mittelwert zu berechnen.
$\text{Definition:}$ Die Kohärenzbandbreite $B_{\rm K}$ (englisch: Coherence Bandwidth ) ist derjenige $\Delta f$–Wert, bei dem der Frequenz–Korrelationsfunktion betragsmäßig erstmals auf die Hälfte abgesunken ist.
- \[\vert \varphi_{\rm F}(\Delta f = B_{\rm K})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm F}(\Delta f = 0)\vert \hspace{0.05cm}.\]
- $B_{\rm K}$ ist ein Maß für die Frequenzdifferenz, um die sich zwei harmonische Schwingungen mindestens unterscheiden müssen, damit sie völlig andere Kanalübertragungseigenschaften vorfinden.
- Ist die Signalbandbreite $B_{\rm S} <B_{\rm K}$, so werden alle Spektralanteile durch den Kanal annähernd gleich verändert.
Das heißt: Genau dann liegt nichtfrequenzselektives Fading vor.
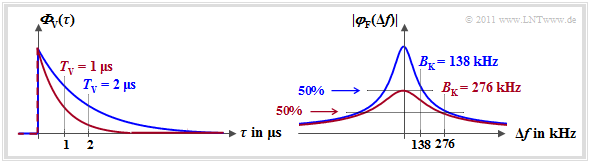
$\text{Beispiel 2:}$ In der Grafik links dargestellt ist die Verzögerungsleistungsdichte ${\it \Phi}_{\rm V}(\tau)$
- mit $T_{\rm V} = 1 \ \rm µs$ (rote Kurve),
- mit $T_{\rm V} = 2 \ \rm µ s$ (blaue Kurve).
In der rechten $\varphi_{\rm F}(\Delta f)$–Darstellung sind die Kohärenzbandbreiten eingezeichnet:
- $B_{\rm K} = 276 \ \rm kHz$ (rote Kurve),
- $B_{\rm K} = 138 \ \rm kHz$ (blaue Kurve).
Man erkennt aus diesen Zahlenwerten:
- Die aus ${\it \Phi}_{\rm V}(\tau)$ berechenbare Mehrwegeverbreiterung $T_{\rm V}$ steht mit der durch $\varphi_{\rm F}(\Delta f)$ festgelegten Kohärenzbandbreite $B_{\rm K}$ in einem festen Verhältnis zueinander: $B_{\rm K} \approx 0.276/T_{\rm V}$.
- Die oft benutzte Näherung $B_{\rm K}\hspace{0.02cm}' \approx 1/T_{\rm V}$ ist hingegen bei exponentiellem ${\it \Phi}_{\rm V}(\tau)$ sehr ungenau.
Betrachten wir nun die Zeitvarianz–Kenngrößen, die von der Zeit–Korrelationsfunktion $\varphi_{\rm Z}(\Delta t)$ bzw. vom Doppler–Leistungsdichtespektrum ${\it \Phi}_{\rm D}(f_{\rm D})$ abgeleitet werden:
$\text{Definition:}$ Die Korrelationsdauer $T_{\rm D}$ (englisch: Coherence Time ) gibt die Zeit an, die im Mittel vergehen muss, bis der Kanal seine Übertragungseigenschaften aufgrund der Zeitvarianz völlig geändert hat. Deren Definition ist ähnlich wie die Definition der Kohärenzbandbreite:
- \[\vert \varphi_{\rm Z}(\Delta t = T_{\rm D})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm Z}(\Delta t = 0)\vert \hspace{0.05cm}.\]
$\text{Definition:}$ Die Dopplerverbreiterung $B_{\rm D}$ (oder „Fading–Bandbreite”, englisch: Doppler Spread ) ist die mittlere Frequenzverbreiterung, die die einzelnen spektralen Signalanteile erfahren. Bei der Berechnung geht man ähnlich vor wie bei der Mehrwegeverbreiterung, indem man die Dopplerverbreiterung $B_{\rm D}$ als die Standardabweichung der Zufallsgröße $f_{\rm D}$ berechnet:
- \[B_{\rm D} = \sigma_{\rm D} = \sqrt{ {\rm E} \left [ f_{\rm D}^2 \right ] - m_{\rm D}^2} \hspace{0.05cm}.\]
- Zunächst ist aus ${\it \Phi}_{\rm D}(f_{\rm D})$ durch Flächennormierung auf $1$ die Doppler–WDF zu ermitteln.
- Daraus ergeben sich die mittlere Dopplerverschiebung $m_{\rm D} = {\rm E}[f_{\rm D}]$ und die Standardabweichung $\sigma_{\rm D}$.
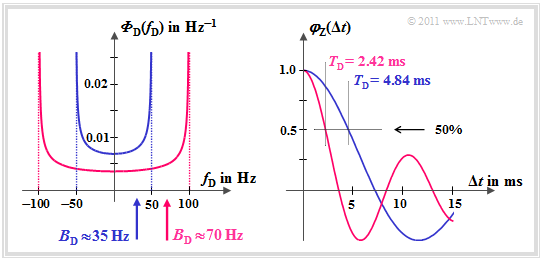
$\text{Beispiel 3:}$ Die Grafik gilt für einen zeitvarianten Kanal ohne Direktkomponente. Links dargestellt ist das Jakes–Spektrum ${\it \Phi}_{\rm D}(f_{\rm D})$.
Die Dopplerverbreiterung $B_{\rm D}$ lässt sich daraus ermitteln:
- \[f_{\rm D,\hspace{0.05cm}max} = 50\,{\rm Hz}\hspace{-0.1cm}: \hspace{-0.1cm}\hspace{0.45cm} B_{\rm D} \approx 35\,{\rm Hz} \hspace{0.05cm},\]
- \[f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz}\hspace{-0.1cm}: \hspace{-0.1cm}\hspace{0.2cm} B_{\rm D} \approx 70\,{\rm Hz} \hspace{0.05cm}.\]
Die Zeitkorrelationsfunktion $\varphi_{\rm Z}(\Delta t)$ als die Fourierrücktransformierte von ${\it \Phi}_{\rm D}(f_{\rm D})$ ist rechts skizziert.
Bei den gegebenen Randbedingungen lautet diese mit der Besselfunktion:
- \[\varphi_{\rm Z}(\Delta t \hspace{-0.05cm} = \hspace{-0.05cm}T_{\rm D}) \hspace{-0.05cm}= \hspace{-0.05cm} {\rm J}_0(2 \pi \hspace{-0.05cm} \cdot \hspace{-0.05cm} f_{\rm D,\hspace{0.05cm}max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\Delta t ).\]
- Die Korrelationsdauer der blauen Kurve ist $T_{\rm D} = 4.84 \ \rm ms$.
- Für $f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz}$ ist die Korrelationsdauer nur halb so groß.
- Allgemein gilt im vorliegenden Fall: $B_{\rm D} \cdot T_{\rm D}\approx 0.17$.
Simulation gemäß dem GWSSUS–Modell
Das abschließend nur kurz dargelegte Monte–Carlo–Verfahren zur Simulation eines GWSSUS–Mobilfunkkanals basiert auf Arbeiten von Rice [Ric44][1] und Höher [Höh90][2].
- Die 2D–Impulsantwort wird durch eine Summe aus $M$ komplexen Exponentialfunktionen dargestellt. $M$ ist als die Anzahl unterschiedlicher Pfade interpretierbar:
- \[h(\tau,\ t)= \frac{1}{\sqrt {M}} \cdot \sum_{m=1}^{M} \alpha_m \cdot \delta (t - \tau_m) \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \phi_{m} }\cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi f_{{\rm D},\hspace{0.05cm} m} t} \hspace{0.05cm}. \]
- Vor Beginn werden die Verzögerungen $\tau_m$, die Dämpfungsfaktoren $\alpha_m$, die gleichverteilten Phasen $\phi_m$ und die Dopplerfrequenzen $f_{{\rm D},\hspace{0.05cm} m}$ nach den GWSSUS–Vorgaben „ausgewürfelt”. Grundlage für das Auswürfeln der Dopplerfrequenzen $f_{{\rm D},\hspace{0.05cm} m}$ ist das Jakes–Spektrum ${\it \Phi}_{\rm D}(f_{\rm D})$, das – geeignet normiert – gleichzeitig die WDF der Dopplerfrequenzen angibt.
- Wegen ${\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})$ ist für alle $m$ die Verzögerungszeit $\tau_m$ unabhängig von der Dopplerfrequenz $f_{{\rm D},\hspace{0.05cm} m}$. Für den terrestrischen Landmobilfunk gilt dies mit guter Näherung. Für das Auswürfeln der Parameter $\alpha_m$ und $\tau_m$, die das Verzögerungs–Leistungsdichtespektrum $ {\it \Phi}_{\rm V}(\tau)$ bestimmen, stehen die COST–Profile $\rm RA$ (Rural Area), $\rm TU$ (Typical Urban), $\rm BU$ (Bad Urban) und $\rm HT$ (Hilly Terrain) zur Verfügung.
- Je größer bei der Simulation die Anzahl $M$ unterschiedlicher Pfade gewählt wird, um so besser wird eine reale Impulsantwort durch obige Gleichung angenähert. Die höhere Simulationsgenauigkeit geht allerdings auf Kosten der Simulationsdauer. In der Literatur werden für $M$ günstige Werte zwischen $100$ und $600$ angegeben.
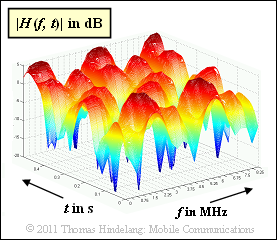
$\text{Beispiel 4:}$ Die Grafik aus [Hin08][3] zeigt ein Simulationsergebnis: Als 2D–Plot ist $20 \cdot \lg \vert H(f, \hspace{0.1cm}t)\vert$ dargestellt, wobei die zeitvariante Übertragungsfunktion $H(f, \hspace{0.1cm}t)$ in diesem Tutorial auch mit $\eta_{\rm FZ}(f, \hspace{0.1cm}t)$ bezeichnet wird.
Der Simulation liegen folgende Parameter zugrunde:
- Die Zeitvarianz entsteht durch eine Bewegung mit $v = 3 \ \rm km/h$.
- Die Trägerfrequenz ist $f_{\rm T} = 2 \ \rm GHz$.
- Die maximale Verzögerungszeit beträgt $\tau_{\rm max} \approx 0.4 \ \rm µ s$.
- Daraus ergibt sich nach der Näherung für die Kohärenzbandbreite $B_{\rm K}\hspace{0.02cm}' \approx 2.5 \ \rm MHz$.
- Die maximale Dopplerfrequenz ist $f_\text{D, max} \approx 5.5 \ \rm Hz$.
- Die Dopplerverbreiterung ergibt sich zu $B_{\rm D} \approx 4 \ \rm Hz$.
Aufgaben zum Kapitel
Aufgabe 2.5Z: Mehrwege-Szenario
Aufgabe 2.6: Einheiten bei GWSSUS
Aufgabe 2.7: Kohärenzbandbreite
Aufgabe 2.7Z: Kohärenzbandbreite des LZI–Zweiwegekanals
Aufgabe 2.8: COST-Verzögerungsmodelle
Aufgabe 2.9: Korrelationsdauer
Quellenverzeichnis
- ↑ Rice, S.O.: Mathematical Analysis of Random Noise. BSTJ–23, pp. 282–232 und BSTJ–24, pp. 45–156, 1945.
- ↑ Höher, P.: Empfang trelliscodierter PSK–Signale auf frequenzselektiven Mobilfunkkanälen – Entzerrung, Decodierung und Kanalschätzung. Düsseldorf: VDI–Verlag, Fortschrittsberichte, Reihe 10, Nr. 147, 1990.
- ↑ Hindelang, T.: Mobile Communications. Vorlesungsmanuskript. Lehrstuhl für Nachrichtentechnik, TU München, 2008.