Frequency Modulation (FM)

1. Modulation Methods
2. Winkelmodulation und WM–Demodulation
3. Frequency Modulation (FM)

• Previous page
• Next page

• Previous page
• Next page

Augenblicksfrequenz (1)

Wir gehen wieder von einem winkelmodulierten Signal aus: $$s(t) = A_{\rm T} \cdot \cos (\psi(t)).$$ Alle Informationen über das Quellensignal $q(t)$ sind damit ausschließlich in der Winkelfunktion $ψ(t)$ enthalten, während die Hüllkurve $a(t) = A_{\rm T}$ konstant ist.

Die Augenblickskreisfrequenz ist die Ableitung der Winkelfunktion nach der Zeit: $$\omega_{\rm A}(t) = \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}\hspace{0.05cm}.$$ Entsprechend gilt für die Augenblicksfrequenz: $$f_{\rm A}(t) = \frac{\omega_{\rm A}(t)}{2\pi} = \frac{1}{2\pi} \cdot \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}\hspace{0.05cm}.$$

Bei einer Winkelmodulation mit der Trägerfrequenz $f_{\rm T}$ schwankt die Augenblicksfrequenz zwischen $$f_{\rm T} - \Delta f_{\rm A} \le f_{\rm A}(t) \le f_{\rm T} + \Delta f_{\rm A}\hspace{0.05cm}.$$

Dabei bezeichnet man die maximale Abweichung $Δf_{\rm A}$ der zeitabhängigen Augenblicksfrequenz $f_{\rm A}(t)$ von der konstanten Trägerfrequenz fT als den Frequenzhub.

Hervorzuheben ist, dass ein grundsätzlicher Unterschied zwischen der Augenblicksfrequenz und dem mit einem Spektrum–Analyzer messbaren Spektrum eines winkelmodulierten Signals besteht, wie das nachfolgende Beispiel verdeutlichen soll.

Augenblicksfrequenz (2)

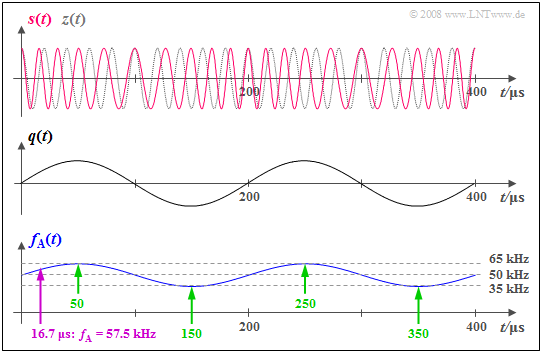
Die Grafik zeigt oben das phasenmodulierte Signal $$s(t) = A_{\rm T} \cdot \cos (\psi(t)) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} \hspace{0.05cm}t + \eta \cdot \sin (2 \pi f_{\rm N} \hspace{0.05cm} t))$$

sowie unten die Augenblicksfrequenz $$f_{\rm A}(t) = \frac{1}{2 \pi} \cdot \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t} = f_{\rm T} + \Delta f_{\rm A}\cdot \cos (2 \pi f_{\rm N} \hspace{0.05cm} t) \hspace{0.05cm}.$$

Die zugrundeliegenden Systemparameter sind $f_{\rm T} =$ 50 kHz, $f_{\rm N} =$ 5 kHz und $η =$ 3. Daraus ergibt sich der Frequenzhub zu $Δf_{\rm A} = η · f_{\rm N} =$ 15 kHz.

In der Mitte ist zur Orientierung der qualitative Verlauf des sinusförmigen Quellensignals $q(t)$ skizziert. Man erkennt aus diesen Grafiken:

• Die Augenblicksfrequenz $f_{\rm A}(t)$ kann alle beliebigen Werte zwischen $f_{\rm T} + Δf_{\rm A} =$ 65 kHz (bei $t =$ 50, 250 μs, usw.) und $f_{\rm T} \ – Δf_{\rm A} =$ 35 kHz (bei $t =$ 150, 350 μs, usw.) annehmen (siehe grüne Markierungen). Zur Zeit $t ≈$ 16.7 μs gilt beispielsweise $f_{\rm A}(t) =$ 57.5 kHz (violetter Pfeil).
• Dagegen besteht die Spektralfunktion $S(f)$ aus diskreten Bessellinien bei den Frequenzen . . . , 30, 35, 40, 45, 50, 55, 60, 65, 70, ... (jeweils in kHz). Eine Spektrallinie bei $f =$ 57.5 kHz gibt es nicht im Gegensatz zu einer Spektrallinie bei $f =$ 70 kHz. Dagegen gilt zu keinem Zeitpunkt $f_{\rm A}(t) =$ 70 kHz.

Ergo: Die Augenblicksfrequenz $f_{\rm A}(t)$ ist also keine physikalisch messbare Frequenz im herkömmlichen Sinne, sondern nur eine fiktive, mathematische Größe, nämlich die Ableitung der Winkelfunktion $ψ(t)$.

Signalverläufe bei Frequenzmodulation

Wie in Kapitel 3.1 gehen wir weiterhin davon aus, dass das Trägersignal $z(t)$ cosinusförmig verläuft und das Quellensignal $q(t)$ spitzenwertbegrenzt ist.

Ist bei einem Übertragungssystem die Augenblickskreisfrequenz $ω_{\rm A}(t)$ linear abhängig vom Momentanwert des Quellensignals $q(t)$, so spricht man von Frequenzmodulation (FM): $$\omega_{\rm A}(t) = 2 \pi \cdot f_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) \hspace{0.05cm}.$$ Hierbei bezeichnet $K_{\rm FM}$ eine dimensionsbehaftete Konstante. Beschreibt $q(t)$ einen Spannungsverlauf, so hat $K_{\rm FM}$ die Einheit $\rm V^{–1}s^{–1}$.

Für die Winkelfunktion und das modulierte Signal erhält man bei FM: $$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm FM} \cdot \int q(t)\hspace{0.1cm}{\rm d}t \hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s(t) = A_{\rm T} \cdot \cos (\psi(t)) \hspace{0.05cm}.$$

Aus dieser Gleichung lässt sich sofort ablesen:

• Auch bei der Frequenzmodulation bewegt sich das äquivalente TP–Signal wegen der konstanten Hüllkurve ⇒ $a(t) = A_{\rm T}$ auf einem Kreisbogen.
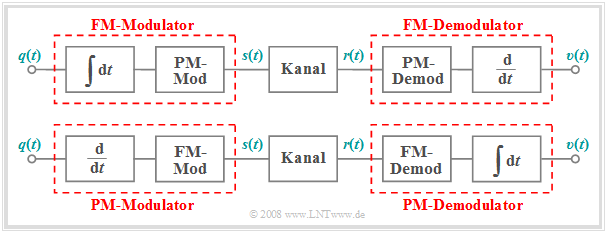
• Ein Frequenzmodulator kann mit Hilfe eines Integrators und eines Phasenmodulators realisiert werden. Der FM–Demodulator besteht demzufolge aus PM–Demodulator und Differenzierer.

Die untere Abbildung zeigt den umgekehrten Zusammenhang, nämlich die mögliche Beschreibung von PM–Modulator und –Demodulator durch die entsprechenden FM–Komponenten.

Man erkennt aus obiger Gleichung auch, dass die im Kapitel 1.3 angegebene Modulatorgleichung im Fall der Frequenzmodulation nur in Sonderfällen gültig sein wird. Die Umwandlung $$s(t) = a(t) \cdot \cos (\omega (t) \cdot t + \phi(t)) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} s(t) = A_{\rm T} \cdot \cos (\omega (t) \cdot t + \phi_{\rm T})$$ ist bei Frequenzmodulation nur manchmal erlaubt, zum Beispiel beim digitalen Modulationsverfahren Frequency Shift Keying (FSK) mit rechteckförmigem Grundimpuls.

Frequenzmodulation eines Cosinussignals (1)

Bei cosinusförmigem Quellensignal $q(t)$ und Frequenzmodulation gilt für die Augenblickskreisfrequenz: $$q(t) = A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)\hspace{0.05cm}.$$

Integriert man diese über die Zeit, so erhält man die Winkelfunktion: $$\psi(t) = \omega_{\rm T} \cdot t + \frac {K_{\rm FM} \cdot A_{\rm N}}{\omega_{\rm N}} \cdot \sin (\omega_{\rm N} \cdot t) \hspace{0.05cm}.$$

Ein Vergleich mit den Aussagen von Kapitel 3.1 macht deutlich:

• Die Frequenzmodulation eines Cosinussignals ergibt qualitativ das gleiche Sendesignal $s(t)$ wie die Phasenmodulation eines sinusförmigen Quellensignals $q(t)$.
• Voraussetzung hierfür ist allerdings, dass die Modulatorkonstanten entsprechend dem Verhältnis $K_{\rm FM}/K_{\rm PM} = ω_{\rm N}$ aneinander angepasst sind.
• Das Sendesignal $s(t)$ lässt sich somit bei den beiden Konstellationen „PM – Sinussignal” sowie „FM – Cosinussignal” einheitlich beschreiben:

$$s(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$

• Allerdings sind bei Anwendung dieser Gleichung für den Modulationsindex $η$ bei Phasen– und Frequenzmodulation unterschiedliche Definitionsgleichungen zu verwenden:

$$\eta_{\rm PM} = {K_{\rm PM} \cdot A_{\rm N}},\hspace{0.5cm}\eta_{\rm FM} = \frac {K_{\rm FM} \cdot A_{\rm N}}{\omega_{\rm N}} \hspace{0.05cm}.$$

• Ist das Quellensignal keine harmonische Schwingung, sondern setzt sich aus mehreren Frequenzen zusammen, so unterscheiden sich die Zeitsignale bei PM und FM auch qualitativ. Dies erkennt man beispielsweise beim Vergleich von PSK und FSK im Kapitel 1.3.

Frequenzmodulation eines Cosinussignals (2)

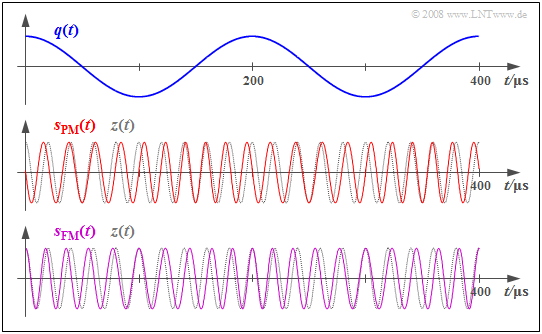
Wir gehen nun von einem cosinusförmigen Quellensignal $q(t)$ mit der Amplitude $A_{\rm N} =$ 3 V und der Frequenz $f_{\rm N} =$ 5 kHz aus und betrachten die Signalverläufe von PM und FM bei gleichem Modulationsindex $η =$ 1.5.

Die mittlere Grafik zeigt das phasenmodulierte Signal für die Modulatorparameter $f_{\rm T} =$ 50 kHz und $K_{\rm PM} = \rm 0.5 V^{–1}$ $$s_{\rm PM}(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t + \eta \cdot \cos (\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$

• Bei PM ergibt sich mit $A_{\rm N} =$ 3 V für den Modulationsindex (oder Phasenhub) $η =$ 1.5 ≈ π/2.
• Die maximale Abweichung der Nulldurchgänge von ihren (äquidistanten) Solllagen beträgt somit etwa ein Viertel der Trägerperiode.
• Ist das Quellensignal $q(t) >$ 0, so kommen die Nulldurchgänge verfrüht, bei $q(t) <$ 0 verspätet.

Die untere Grafik zeigt das frequenzmodulierte Signal mit gleichem Modulationsindex $η$: $$s_{\rm FM}(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t)) \hspace{0.05cm}.$$

Erreicht wird in diesem Fall $η =$ 1.5 beispielsweise durch die Modulatorkonstante $$K_{\rm FM} = \frac {\eta \cdot \omega_{\rm N}}{A_{\rm N}} = {K_{\rm PM} \cdot \omega_{\rm N}} = 0.5\,{\rm V}^{-1} \cdot 2 \pi \cdot 5\,{\rm kHz} = 15708\,{\rm V}^{-1}{\rm s}^{-1} \hspace{0.05cm}.$$

• Der Frequenzhub beträgt hier $Δf_{\rm A} = η · f_{\rm N} =$ 7.5 kHz, und es treten Augenblicksfrequenzen zwischen 42.5 und 57.5 kHz auf.
• Die Nulldurchgänge stimmen nun bei den Maxima und den Minima des Quellensignals $q(t)$ mit denen des Trägersignals $z(t)$ überein, während die maximalen Phasenabweichungen bei den Nulldurchgängen von $q(t)$ zu erkennen sind.

WM–Spektrum einer harmonischen Schwingung (1)

Nun setzen wir für das Quellensignal allgemein eine harmonische Schwingung mit der Phase ${\mathbf ϕ}_{\rm N}$ voraus: $$q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t + \phi_{\rm N}).$$ Uns interessiert die Spektralfunktion $S(f)$. Zur einfacheren Darstellung betrachten wir im Folgenden das Betragsspektrum $|S_+(f)|$ des analytischen Signals, aus dem $|S(f)|$ in der bekannten Weise hergeleitet werden kann. Für jede Art von Winkelmodulation in der hier beschriebenen Weise – egal, ob Phasen– oder Frequenzmodulation – und auch unabhängig von der Phase ${\mathbf ϕ}_{\rm N}$ des Quellensignals gilt: $$|S_{\rm +}(f)| = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}|{\rm J}_n (\eta)| \cdot \delta [f - (f_{\rm T} + n \cdot f_{\rm N})]\hspace{0.05cm}.$$

Diese Gleichung lässt sich wie folgt begründen:

• Auf der Seite 4 im Abschnitt 3.1 wurde diese Gleichung für ein phasenmoduliertes Sinussignal abgeleitet, wobei $η = A_{\rm N} · K_{\rm PM}$ den Modulationsindex angibt und $J_n(η)$ die Besselfunkton erster Art und $n$–ter Ordnung bezeichnet. $K_{\rm PM}$ ist die Modulatorkonstante.
• Durch eine andere Nachrichtenphase ${\mathbf ϕ}_{\rm N}$ ändert sich nur die Phasenfunktion arg $S_+(f)$, nicht aber das Betragsspektrum $|S_+(f)|$. Dieses wichtige Ergebnis wurde auch durch die Aufgabe Z3.3 im Kapitel 3.1 bestätigt.
• Auf Seite 3 dieses Abschnittes wurde gezeigt, dass ein FM–Signal in gleicher Weise wie ein PM–Signal dargestellt werden kann, wenn der Modulationsindex $η = K_{\rm FM} · A_{\rm N}/ω_{\rm N}$ verwendet wird. Folgerichtig sind auch die Betragsspektren bei PM und FM in gleicher Form darstellbar.

WM–Spektrum einer harmonischen Schwingung (2)

Wir betrachten wieder eine harmonische Schwingung mit der Amplitude $A_{\rm N} =$ 3 V nach

• einer Phasenmodulation (mit $K_{\rm PM} = \rm 0.5 V^{–1}$),
• einer Frequenzmodulation (mit $K_{\rm FM} = \rm 15708 V^{–1}s^{–1}$).

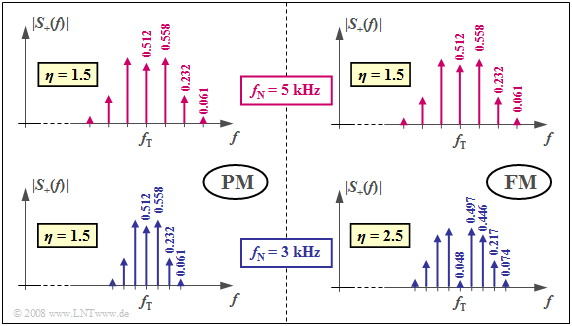
Die zugehörigen Signalverläufe sind im Abschnitt 3b dargestellt. Bei beiden Systemen ergibt sich für $f_{\rm N} =$ 5 kHz ein Besselspektrum mit dem Modulationsindex $η =$ 1.5. Die identischen Betragsspektren des analytischen Signals (nur positive Frequenzen) sind in der oberen Bildhälfte dargestellt. Bessellinien mit Werten kleiner als 0.03 sind hierbei vernachlässigt.

Die beiden unteren Bilder gelten für die Nachrichtenfrequenz $f_{\rm N} =$ 3 kHz. Man erkennt:

• Bei der Phasenmodulation ergibt sich gegenüber $f_{\rm N} =$ 5 kHz eine schmalere Spektralfunktion, da nun der Abstand der Bessellinien nur mehr 3 kHz beträgt. Da sich der Modulationsindex $η =$ 1.5 nicht ändert, ergeben sich die gleichen Besselgewichte wie bei $f_{\rm N} =$ 5 kHz.
• Auch bei der Frequenzmodulation treten nun die Bessellinien im Abstand von 3 kHz auf. Es gibt aber nun aufgrund des größeren Modulationsindex $η =$ 2.5 – dieser ist umgekehrt proportional zu $f_{\rm N}$ – deutlich mehr Bessellinien als im rechten oberen (für $η =$ 1.5 gültigen) Diagramm.

Einfluss einer Bandbegrenzung bei Winkelmodulation (1)

Fassen wir einige Resultate dieses Abschnittss kurz zusammen, wobei wir beispielhaft die Trägerfrequenz $f_{\rm T} =$ 100 kHz, die Nachrichtenfrequenz $f_{\rm N} =$ 5 kHz und den Modulationsindex $η =$ π/2 voraussetzen:

• Das Spektrum einer winkelmodulierten Schwingung besteht aus Bessellinien um den Träger $f_{\rm T}$ im Abstand $f_{\rm N}$ der Nachrichtenfrequenz und ist theoretisch unendlich weit ausgedehnt.

• Selbst wenn man alle Spektrallinien mit Beträgen kleiner als 0.01 vernachlässigt, beträgt die dann endliche Bandbreite für $η =$ π/2 noch immer $B_{\rm HF} = 8 · f_{\rm N} =$ 40 kHz.

• Die Ortskurve – also der Verlauf des äquivalenten TP–Signals in der komplexen Ebene – ist im Idealfall ein Kreisbogen mit einem Öffnungswinkel von ±1.57 rad = ±90°.

• Der Kreisbogen nach vektorieller Addition ergibt sich allerdings nur dann, wenn alle Bessellinien in der Ortskurve mit den richtigen Zeigerlängen, Phasenlagen und Kreisfrequenzen rotieren.

• Logischerweise wird die halbkreisförmige Ortskurve verändert, wenn Spektrallinien verfälscht werden (z. B. durch lineare Kanalverzerrungen) oder ganz fehlen (z. B. durch Bandbegrenzung).

• Da der ideale Winkeldemodulator die Phase ${\mathbf ϕ}_r(t)$ des Empfangssignals detektiert und daraus das Sinkensignal $υ(t)$ gewinnt, wird dieses verfälscht und zwar sogar nichtlinear ⇒ irreversibel.

• Das bedeutet gleichzeitig: Aufgrund linearer Verzerrungen im Kanal kommt es zu nichtlinearen Verzerrungen im demodulierten Signal ⇒ es entstehen dadurch neue Frequenzen (Oberwellen).

• Je kleiner die zur Verfügung stehende Bandbreite $B_{\rm HF}$ ist und je größer der Modulationsindex $η$ gewählt wird, desto größer wird der die nichtlinearen Verzerrungen beschreibende Klirrfaktor $K$.

• Als Faustformel für die erforderliche HF–Bandbreite für einen geforderten Klirrfaktor $K$ gilt:

$$K < 10\%: B_{\rm HF} \ge 2 \cdot f_{\rm N} \cdot (\eta +1)\hspace{0.05cm},$$ $$K < 1\%\hspace{0.12cm}: B_{\rm HF} \ge 2 \cdot f_{\rm N} \cdot(\eta +2)\hspace{0.05cm}.$$

Man bezeichnet diesen näherungsweisen Zusammenhang zwischen der HF–Bandbreite und dem Klirrfaktor auch als Carson–Regel.

Einfluss einer Bandbegrenzung bei Winkelmodulation (2)

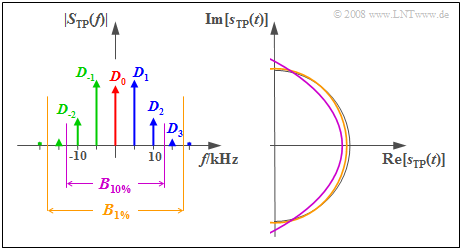
Wir gehen weiterhin von den Systemparametern $f_{\rm T} =$ 100 kHz, $f_{\rm N} =$ 5 kHz und $η = $ π/2 aus. Die Grafik zeigt für diesen Fall links das Betragsspektrum $|S_{\rm TP}(f)|$ des äquivalenten TP–Signals und rechts die zugehörige Zeitfunktion $s_{\rm TP}(t)$.

Um den Klirrfaktor $K$ auf Werte kleiner als 1% zu begrenzen, ist nach der sog. Carson–Regel die HF–Bandbreite $B_{1 \%} ≈$ 36 kHz erforderlich. In diesem Fall setzt sich das äquivalente TP–Signal $$\begin{align*}r_{\rm TP}(t) & = \sum_{n = - 3}^{+3}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.02cm}\cdot \hspace{0.05cm} t }\end{align*}$$

aus der Konstanten $D_0$ und je drei entgegen dem Uhrzeigersinn $(D_1, D_2, D_3)$ bzw. im Uhrzeigersinn $(D_{-1}, D_{-2}, D_{-3})$ drehenden Zeigern zusammen. Die ockerfarbene Kurve in der Zeitbereichsdarstellung macht deutlich, dass sich das äquivalente TP-Signal durch diese Bandbegrenzung nur geringfügig vom (verzerrungsfreien) Halbkreis unterscheidet.

Gibt man sich mit einem Klirrfaktor $K <$ 10% zufrieden, so ist die HF–Bandbreite $B_{10 \%} ≈$ 26 kHz ausreichend. Damit werden auch die Fourierkoeffizienten $D_3$ und $D_{-3}$ abgeschnitten und die violett dargestellte Ortskurve beschreibt einen Parabelabschnitt. Die Simulation dieses Fallbeispiels liefert den Klirrfaktor $K ≈$ 6%. Das heißt, dass die Carson–Regel oft ein etwas zu pessimistisches Ergebnis liefert.